Dynamic programming in practice.
This is my first article on a similar subject, so please treat with understanding. I will welcome any comments and observations.
I think many of you have heard, and many have even encountered this method of solving certain problems, like the dynamic programming method. For those who do not know, here is the definition of Wikipedia:
Pretty good and clear explanation, but let's take an example. I think the simplest thing that comes to mind is the Fibonacci numbers. Some initial data are given for it - A [1] = 1, A [2] = 1, in after the element A [i] = A [i-1] + A [i-2]. In this case, A [i] is often referred to as a state , and some relation with respect to the pre-calculated data is referred to as a transition . In this case, there are 2 transitions from A [i] - to A [i-1] and to A [i-2]. The number of transitions may vary depending on the task.
But dynamic programming is not just used. Namely, because it sometimes allows a very significant reduction in the time it takes to solve a task, which sometimes, with large amounts of input data, is very critical. And I want to show one such task that I met at the School Olympics Zonal this year. Literally, I do not remember the condition, but here’s a general meaning:
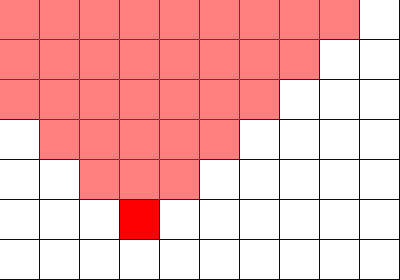
So, to find out the value of elements in a string, we need to know the values of the elements in all the lines above it. The simplest solution that comes to mind is for each element to simply take and go through all the elements in the triangle above it, counting the sum. Yes, this can be done when time is not critical or when the restrictions on N and M are small, because such an algorithm works for the asymptotics of order O (N 4 ) (if we take N = M). Those. even if N = M = 100, this will work for about 5-10 seconds (depending on the computer), I am already silent about N = M = 2000. So, we need to accelerate this matter somehow. And let's do this. We have a triangle to calculate. And we have pre-calculated triangles for all the elements above it. So let's make a new triangle, using the already calculated! See the picture:

Those. if we need to calculate a triangle starting at A [i, j], then it will be calculated by the formula:
A [i, j] = (A [i-1, j] + 2 * A [i-1, j-1] + 2 * A [i-1, j + 1] -2 * A [i-2 , j]) mod K. (where mod K is to take modulo K)
We subtract the triangle A [i-2, j] because this is the intersection of two triangles A [i-1, j-1] and A [i-1, j + 1] and otherwise we would count it 2 times. By the way, think for yourself why we multiply some values by 2.
The general idea of this problem is this. Try to write your own solution (there are several nuances in it, which I suggest you find yourself) and test it with the help of the usual re-selection algorithm on different tests. If anything is unclear - contact me, I will try to help, although, I must admit, I myself am far from a pro in this business and I can solve not all tasks, but I can do something ;-)
I think many of you have heard, and many have even encountered this method of solving certain problems, like the dynamic programming method. For those who do not know, here is the definition of Wikipedia:
The idea of dynamic programming is to partition the problem into several independent subtasks, solve each of them, and then calculate the original result. To solve subtasks the same algorithm is applied recursively. In this case, for each subtask the calculated answer is remembered, and if at some step the subtask is encountered a second time, then calculations are not performed for it.
http://ru.wikipedia.org/wiki/Dynamic_programming
Pretty good and clear explanation, but let's take an example. I think the simplest thing that comes to mind is the Fibonacci numbers. Some initial data are given for it - A [1] = 1, A [2] = 1, in after the element A [i] = A [i-1] + A [i-2]. In this case, A [i] is often referred to as a state , and some relation with respect to the pre-calculated data is referred to as a transition . In this case, there are 2 transitions from A [i] - to A [i-1] and to A [i-2]. The number of transitions may vary depending on the task.
But dynamic programming is not just used. Namely, because it sometimes allows a very significant reduction in the time it takes to solve a task, which sometimes, with large amounts of input data, is very critical. And I want to show one such task that I met at the School Olympics Zonal this year. Literally, I do not remember the condition, but here’s a general meaning:
There is a matrix of numbers A of size NxM and number K. Its first row is given - A [1,1] .. A [1, M]. After that, for each element below the first row, the value is defined as the sum of all elements in a triangle above it modulo K. It is required to output the last row of this matrix A [N, 1] .. A [N, M]. Limitations: 1 ≤ N, M ≤ 2000; 2 ≤ K ≤ 10 9 .
So, to find out the value of elements in a string, we need to know the values of the elements in all the lines above it. The simplest solution that comes to mind is for each element to simply take and go through all the elements in the triangle above it, counting the sum. Yes, this can be done when time is not critical or when the restrictions on N and M are small, because such an algorithm works for the asymptotics of order O (N 4 ) (if we take N = M). Those. even if N = M = 100, this will work for about 5-10 seconds (depending on the computer), I am already silent about N = M = 2000. So, we need to accelerate this matter somehow. And let's do this. We have a triangle to calculate. And we have pre-calculated triangles for all the elements above it. So let's make a new triangle, using the already calculated! See the picture:

Those. if we need to calculate a triangle starting at A [i, j], then it will be calculated by the formula:
A [i, j] = (A [i-1, j] + 2 * A [i-1, j-1] + 2 * A [i-1, j + 1] -2 * A [i-2 , j]) mod K. (where mod K is to take modulo K)
We subtract the triangle A [i-2, j] because this is the intersection of two triangles A [i-1, j-1] and A [i-1, j + 1] and otherwise we would count it 2 times. By the way, think for yourself why we multiply some values by 2.
The general idea of this problem is this. Try to write your own solution (there are several nuances in it, which I suggest you find yourself) and test it with the help of the usual re-selection algorithm on different tests. If anything is unclear - contact me, I will try to help, although, I must admit, I myself am far from a pro in this business and I can solve not all tasks, but I can do something ;-)
')
Source: https://habr.com/ru/post/22514/
All Articles