Chasing the chairs
In the next post, an interesting problem was presented, the condition of which is as follows:
The probability that diamonds are sewn into one of the twelve chairs is 0.9. Assuming that the chairs are opened one after the other, and the next one is passed only if there are no diamonds in the current chair, find the probability that the diamonds will be at 12 in the account chair.
For the near future, let us abstract from the exact numerical values and set the probability that diamonds are sewn equal to p, and the number of chairs is n.
')
Want to know the right solution to this problem? Welcome under the cut!
So let's start from afar. First of all, we find the probability that the diamonds are in the first chair. Using the formula of total probability. we find
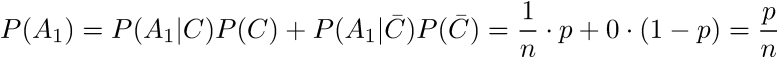
Since we are not checking the chairs at the same time, but in order, we will open the second chair only if there is nothing in the first one:
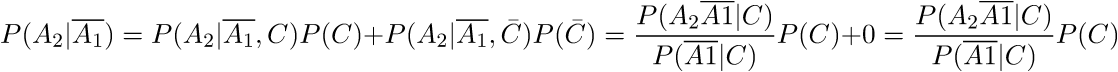
Here there is a great temptation to reveal the numerator of the resulting fraction according to the rule of the product of probabilities, but this cannot be done. We check the chairs in turn, which means that our events are not independent. Since diamonds, if laid, can be equally likely to be in any of the twelve chairs, the probability of an event will be:
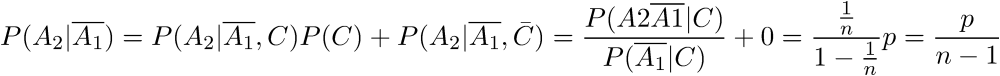
Making a new iteration, we get:
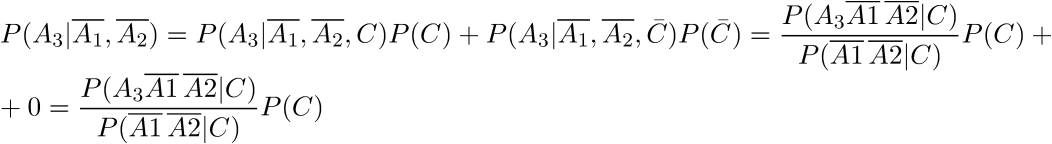
Again, the events in the denominator are not independent, and we do not have the right to apply the formula of the product of probabilities, but we can use the formula for adding probabilities:
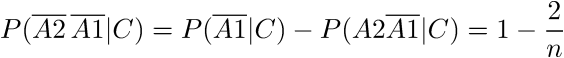
As a result, we get the formula:

Now it is easy to see that the final formula for the probability that the diamond is sewn up in the kth chair has the form:
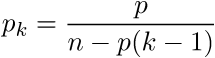
Substitute the original values: p = 0.9 and n = 12. As a result, we get the answer: 0. (428571) or 42.85%.
Special thanks I want to express to the user mayorovp, who noticed an error in the calculations, which I made with inattention. With all my heart, I want to wish that only the brightest people could meet on his way. Best regards, ProPupil.
The probability that diamonds are sewn into one of the twelve chairs is 0.9. Assuming that the chairs are opened one after the other, and the next one is passed only if there are no diamonds in the current chair, find the probability that the diamonds will be at 12 in the account chair.
For the near future, let us abstract from the exact numerical values and set the probability that diamonds are sewn equal to p, and the number of chairs is n.
')
Want to know the right solution to this problem? Welcome under the cut!
So let's start from afar. First of all, we find the probability that the diamonds are in the first chair. Using the formula of total probability. we find
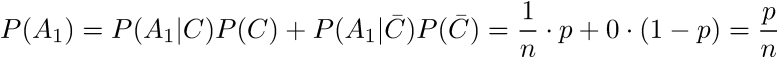
Since we are not checking the chairs at the same time, but in order, we will open the second chair only if there is nothing in the first one:
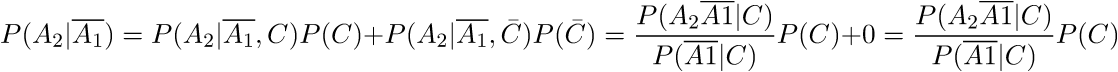
Here there is a great temptation to reveal the numerator of the resulting fraction according to the rule of the product of probabilities, but this cannot be done. We check the chairs in turn, which means that our events are not independent. Since diamonds, if laid, can be equally likely to be in any of the twelve chairs, the probability of an event will be:
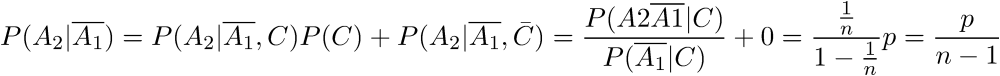
Making a new iteration, we get:
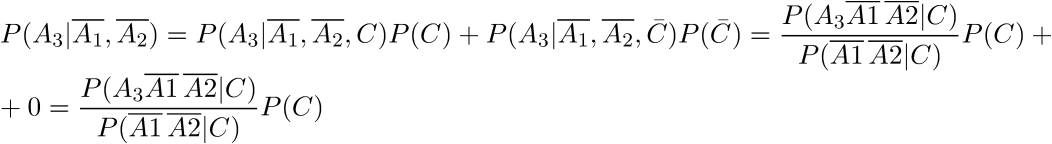
Again, the events in the denominator are not independent, and we do not have the right to apply the formula of the product of probabilities, but we can use the formula for adding probabilities:
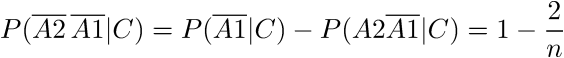
As a result, we get the formula:

Now it is easy to see that the final formula for the probability that the diamond is sewn up in the kth chair has the form:
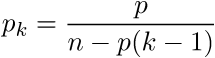
Substitute the original values: p = 0.9 and n = 12. As a result, we get the answer: 0. (428571) or 42.85%.
Special thanks I want to express to the user mayorovp, who noticed an error in the calculations, which I made with inattention. With all my heart, I want to wish that only the brightest people could meet on his way. Best regards, ProPupil.
Source: https://habr.com/ru/post/225031/
All Articles