Factor analysis for dummies
I think many of us, at least once were interested in artificial intelligence and neural networks. In the theory of neural networks, factor analysis is far from the last. It is designed to highlight the so-called hidden factors. This analysis has many methods. The method of principal components stands apart, the distinctive feature of which is a complete mathematical justification. Frankly, when I started reading articles on the links above, I felt uncomfortable because I did not understand anything. My interest subsided, but, as is usually the case, understanding has come by itself, out of the blue.
So, let's consider the Arabic numbers from 0 to 9. In this case, the 5x7 format, which was taken from the project under the LCD from Nokia 3310.
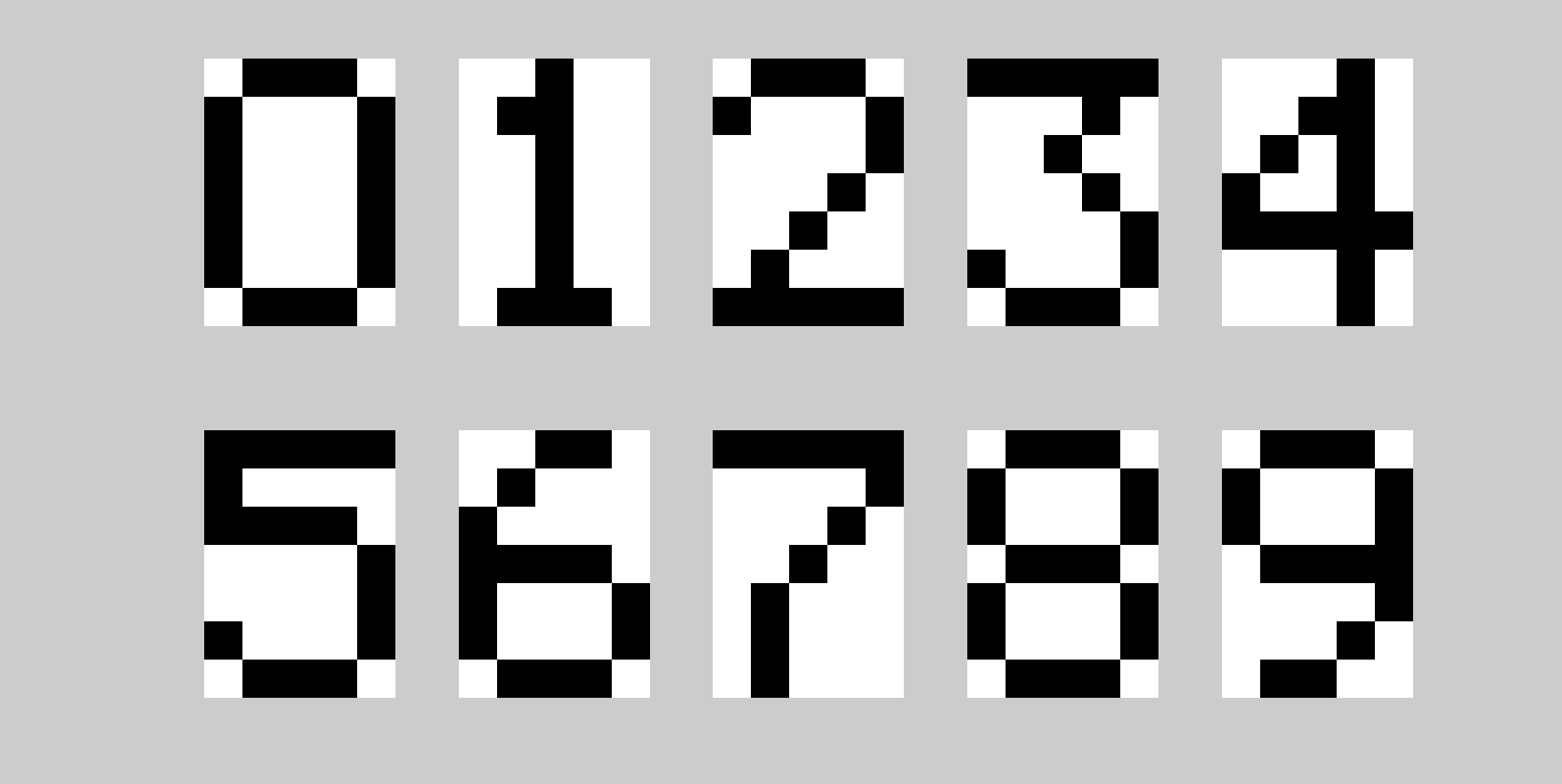
Black pixels correspond to 1, white - 0. Thus, we can represent each digit in the form of a 5x7 matrix. For example, the matrix below:
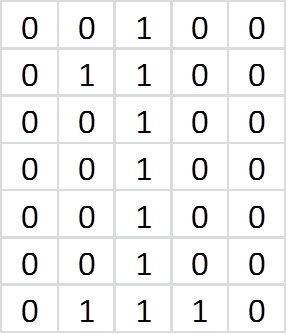
matches the picture:
')
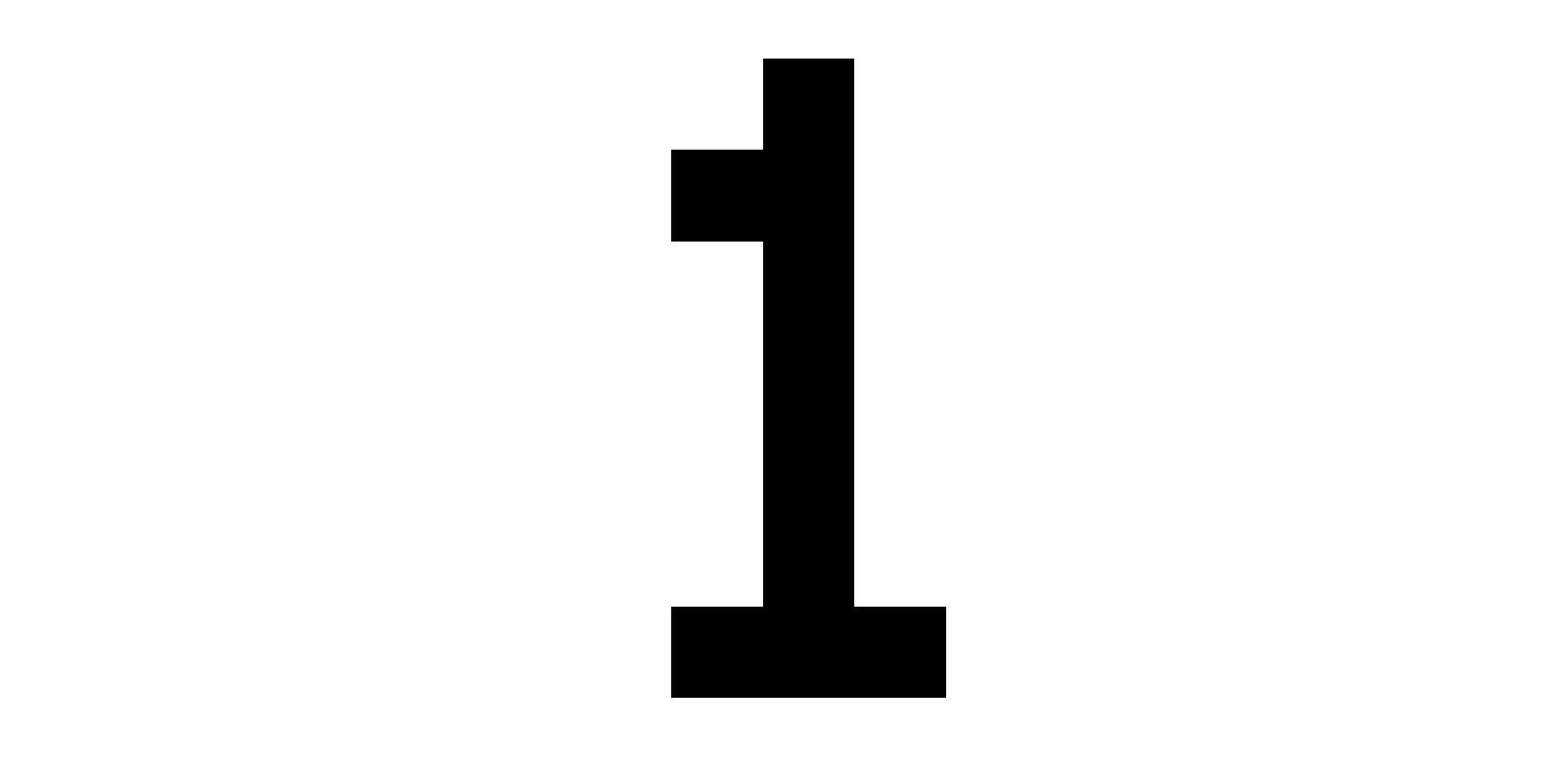
Let's sum up the pictures for all the digits, and normalize the resulting one. This means getting a 5x7 matrix, the cells of which contain the sum of the same cells for different digits divided by their number. As a result, we get the picture:

Matrix for her:

The darkest areas immediately catch the eye. There are three of them, and they correspond to a value of 0.9 . This is what they look like. What is common to all numbers. The probability of meeting the black pixel in these places is high. Let's look at the brightest areas. There are also three of them, and they correspond to a value of 0.1 . But again, this is what all the numbers look like, what is common to them all. The probability of meeting the white pixel in these places is high. What are they different? And the maximum difference between them in places with a value of 0.5 . The color of the pixel in these places is equally likely. Half of the numbers in these places will be black, half - white. Let's analyze these places, since we have only 6 of them.
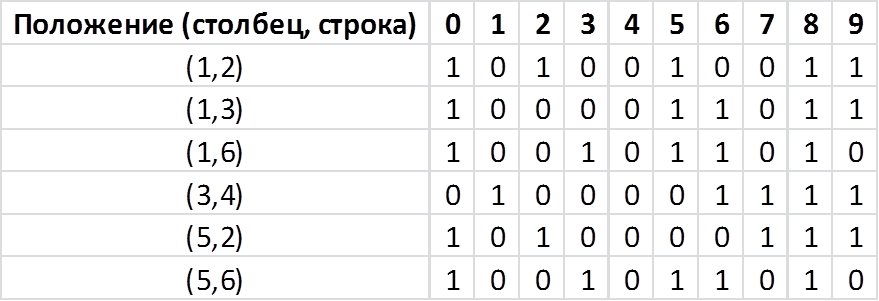
The position of a pixel is definitely column and row. The counting starts from 1, the direction for the row from top to bottom, for the column from left to right. The remaining cells have a pixel value for each digit in the specified position. Now let's select the minimum number of positions for which we can still distinguish numbers. In other words, for which the values in the columns will be different. Since we have 10 digits, and we code them binary, at least 4 combinations of 0 and 1 (log (10) / log (2) = 3.3) are mathematically necessary. Let's try to select 4 out of 6 that would satisfy our condition:
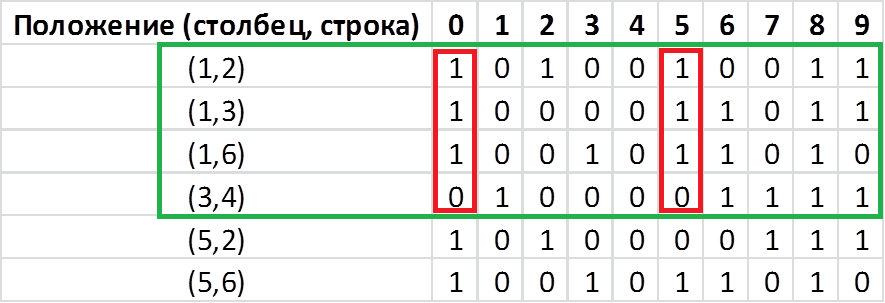
As you can see the value in columns 0 and 5 are the same. Consider another combination:
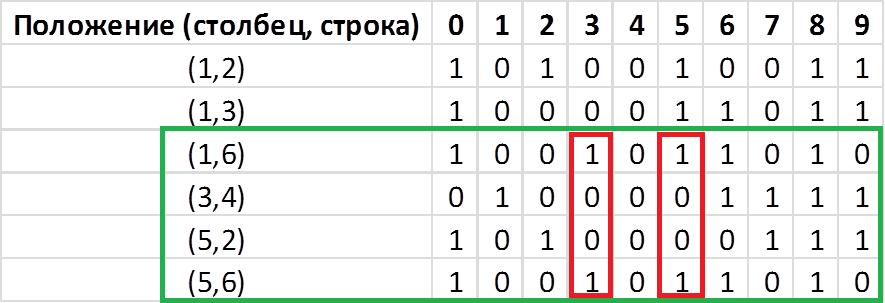
There are also matches between columns 3 and 5. Consider the following:
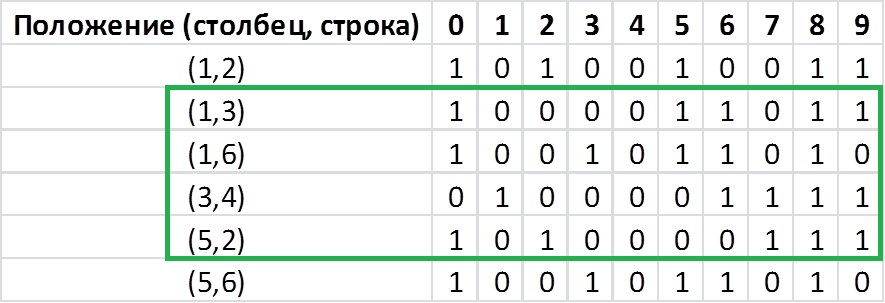
And here are no collisions. Bingo! And now I will tell you why all this was started:

Suppose with each pixel, of which we have 5x7 = 35, the signal enters a black box, and the output is a signal that corresponds to the input digit. And what happens in the black box? And in the black box from all 35 signals, those 4 are selected that are fed to the input of the decoder and allow you to uniquely identify the number at the input. Now it is clear why we were looking for combinations without matches. After all, if 4 signals of the first combination were selected in the black box, the digits 0 and 5 for such a system would simply not be distinguishable. We minimized the task, because instead of 35 signals it is enough to process only 4. Those 4 pixels are the minimum set of hidden factors that characterize this array of numbers. This set has a very interesting feature. If you look at the values in the columns, you can see that the figure 8 is the opposite of the number 4, 7 - 5, 9 - 3, 6 - 2, and 0 - 1. Attentive reader will ask, and where does neural networks? A feature of neural networks is that it itself is able to isolate these factors, without the intervention of a reasonable person. You just periodically show her the numbers, and she finds those 4 hidden signals and commutes with one of her 10 outputs. How can we apply the similar signals that we discussed at the beginning? And they can serve as a label set of numbers. For example, Roman numerals will have their own set of highs and lows, and letters - their own. According to the signals of similarity, you can separate the numbers from the letters, but it is possible to recognize the characters within the set only by the maximum difference.
So, let's consider the Arabic numbers from 0 to 9. In this case, the 5x7 format, which was taken from the project under the LCD from Nokia 3310.
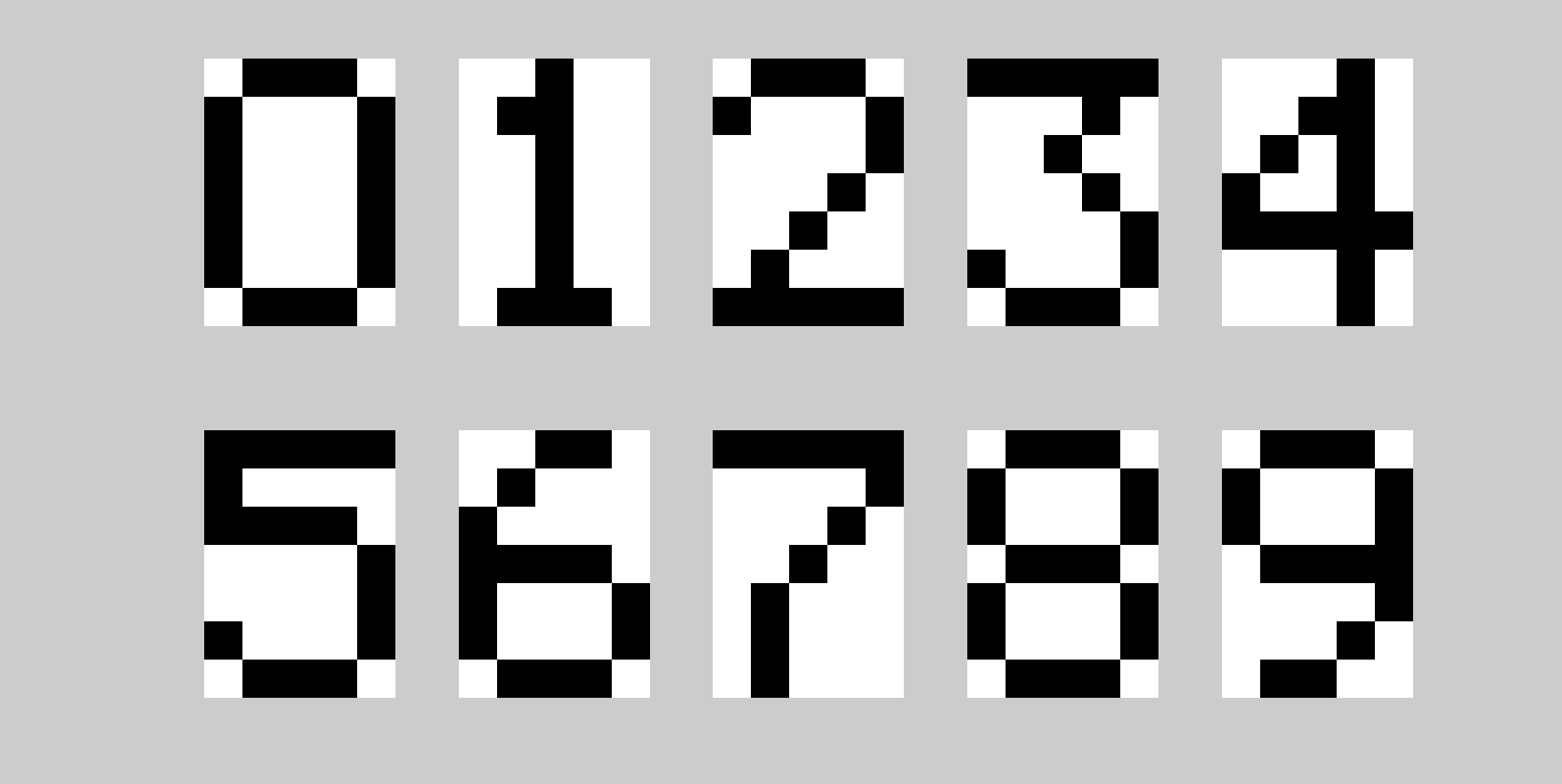
Black pixels correspond to 1, white - 0. Thus, we can represent each digit in the form of a 5x7 matrix. For example, the matrix below:

matches the picture:
')
Let's sum up the pictures for all the digits, and normalize the resulting one. This means getting a 5x7 matrix, the cells of which contain the sum of the same cells for different digits divided by their number. As a result, we get the picture:

Matrix for her:

The darkest areas immediately catch the eye. There are three of them, and they correspond to a value of 0.9 . This is what they look like. What is common to all numbers. The probability of meeting the black pixel in these places is high. Let's look at the brightest areas. There are also three of them, and they correspond to a value of 0.1 . But again, this is what all the numbers look like, what is common to them all. The probability of meeting the white pixel in these places is high. What are they different? And the maximum difference between them in places with a value of 0.5 . The color of the pixel in these places is equally likely. Half of the numbers in these places will be black, half - white. Let's analyze these places, since we have only 6 of them.

The position of a pixel is definitely column and row. The counting starts from 1, the direction for the row from top to bottom, for the column from left to right. The remaining cells have a pixel value for each digit in the specified position. Now let's select the minimum number of positions for which we can still distinguish numbers. In other words, for which the values in the columns will be different. Since we have 10 digits, and we code them binary, at least 4 combinations of 0 and 1 (log (10) / log (2) = 3.3) are mathematically necessary. Let's try to select 4 out of 6 that would satisfy our condition:

As you can see the value in columns 0 and 5 are the same. Consider another combination:

There are also matches between columns 3 and 5. Consider the following:

And here are no collisions. Bingo! And now I will tell you why all this was started:

Suppose with each pixel, of which we have 5x7 = 35, the signal enters a black box, and the output is a signal that corresponds to the input digit. And what happens in the black box? And in the black box from all 35 signals, those 4 are selected that are fed to the input of the decoder and allow you to uniquely identify the number at the input. Now it is clear why we were looking for combinations without matches. After all, if 4 signals of the first combination were selected in the black box, the digits 0 and 5 for such a system would simply not be distinguishable. We minimized the task, because instead of 35 signals it is enough to process only 4. Those 4 pixels are the minimum set of hidden factors that characterize this array of numbers. This set has a very interesting feature. If you look at the values in the columns, you can see that the figure 8 is the opposite of the number 4, 7 - 5, 9 - 3, 6 - 2, and 0 - 1. Attentive reader will ask, and where does neural networks? A feature of neural networks is that it itself is able to isolate these factors, without the intervention of a reasonable person. You just periodically show her the numbers, and she finds those 4 hidden signals and commutes with one of her 10 outputs. How can we apply the similar signals that we discussed at the beginning? And they can serve as a label set of numbers. For example, Roman numerals will have their own set of highs and lows, and letters - their own. According to the signals of similarity, you can separate the numbers from the letters, but it is possible to recognize the characters within the set only by the maximum difference.
Source: https://habr.com/ru/post/224495/
All Articles