Splitting algorithms and van der Waerden numbers
Hi, Habr! I decided to indulge in graphomania and share the result of last weekend's entertainment (only this weekend passed a long time ago and the article was written much longer than entertainment. As they say, time is fun for an hour).
I will talk about the so-called splitting algorithms (in particular, about the DPLL algorithm), about the theorem and van der Waerden numbers, and in conclusion of the article we will write our own splitting algorithm and in half an hour of calculations we will prove that the number w (2; 5 ) equal to 178 (pioneers in 1978, it took more than 8 days of calculations).
This is a fairly general algorithm that solves the following problem: there is some finite set S and we want to divide it into two subsets A and B, with some properties, or to determine that the set S cannot be divided in the necessary way.
This is done in the following way: 3 non-intersecting subsets A, B, C are supported, which completely cover the set S, where C is the set of those elements that we have not yet distributed between A and B. Initially, C = S, and A and B are empty. At each iteration in the set C, the element a is arbitrarily chosen, which can be placed either in the set A or in the set B. In fact, we do both, and then recursively process both possible options.
')
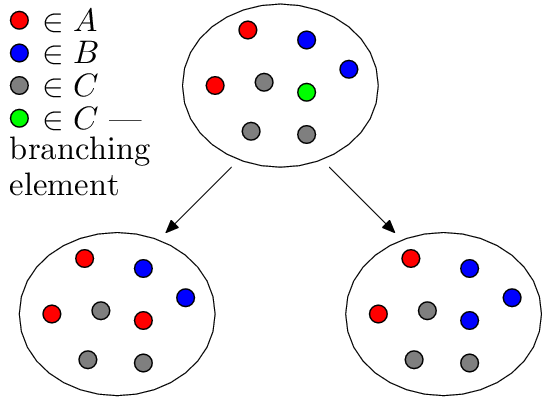
The result is a splitting tree, the leaves of which contain all sorts of divisions of the set S into A and B, and the set C is empty. Now we just need to check for all leaves that the properties of interest to us.
“Allow me!”, You will say, “than this is better than the obvious brute force of 2 | S | options? And the whole thing in the cutoffs, which are very convenient to add to the above proposed core of the algorithm!
List of cuts:
With the use of clippings, the size of the tree is greatly reduced, the number of leaves decreases noticeably, sometimes to 0 (this means that it is impossible to divide S into A and B as appropriate). Although the complexity of the algorithm still remains exponential at worst.
It is convenient to explain the general splitting algorithm and all the proposed cut-offs using the example of the classical DPLL algorithm.
The Davis – Putnam – Laugemann – Loveland algorithm (DPLL) was developed in 1962 to determine the feasibility of Boolean formulas written in conjunctive normal form, i.e. to solve the problem of SAT. The algorithm turned out to be so efficient that after more than 50 years it is the basis for the majority of effective SAT solvers.
Let's take a closer look at what the DPLL algorithm does. He takes the Boolean formula and tries to divide all the variables in it into two sets A and B, where A is the set of all variables with a value of true and B is the set of all variables with a value of false.
At each step, a variable is selected in some way, which has not yet been assigned a value (let's call such variables free ) and is assigned the value true (this variable is entered into the set A). After that, the resulting simplified problem is solved. If it is doable, then the original formula is doable. Otherwise, the selected variable is assigned the value false (it is entered in B) and the problem is solved for the new simplified formula. If it is doable, then the original formula is doable. Otherwise - alas, the original formula is impracticable.
After each assignment, the formula is further simplified using the following two rules:
These two rules should be applied as long as they are applied: usually after the first assignment, a whole cascade of simplifications follows, which well reduces the number of free variables.
If, after simplification, we have received an empty clause (all its simple conjuncts are false) - the current formula is not feasible and should be rolled back. If there are no free variables left, then the formula is feasible and the work of the algorithm can be completed. You can also finish the work of the algorithm if the clause is not left - you can assign unused free variables in an arbitrary way.
A small C-like pseudocode explaining what happens:
The & symbol shows that in the function unit_propagation and pure_literal_elimination, the variables F, A, B and C are passed by reference, i.e. they can change inside. If anything has changed, these functions return true. When recursive descent - on the contrary, copies of objects are created. The ^ icon excludes an object from the set if it exists or adds if it does not exist.
Consider the following formula and, using its example, let's see how the DPLL algorithm works:
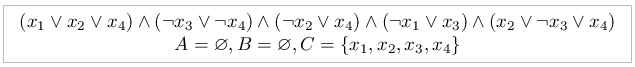
The simplification rules do not apply to this formula, so we will have to branch our tree. As an element for branching, we take x 1 and, for a start, assign it the value true. We get the following chain of simplifications:

Double arrows show that we use the first rule, namely, we find a lonely variable and assign it the desired value.
Unfortunately, this branch leads to an impracticable formula, i.e. In this branch, we tried in vain. We roll back and try to set the variable x 1 to false. This will lead to the following chain of simplifications:

Triple arrows indicate that we apply the second rule of simplification. Success is waiting for us in this branch - 2 solutions were found!
Whole walk tree:

Since the transformations shown by double and triple arrows occur inside each vertex of the tree, it turns out that the tree itself actually consists of only three vertices! However, it was probably possible to come up with a more intricate example.
Note that if, at the very beginning, for the branching, for example, the element x 2 was chosen, then the desired tree would have been much smaller and the answer would have been found much earlier (the necessary calculations are proposed to be made to the reader independently). Therefore, the element selection strategy for branching is very important. For example, you can choose to branch a variable that is included in the largest number of clauses.
It is also worth noting that with the help of this algorithm it is impossible to find all the solutions - this is prevented by the heuristic of the exclusion of “pure” variables. It may well be missing a solution in which the value of the variable that we, following the heuristic, set to true, is false. To search for all solutions, the second rule should be excluded from the algorithm.
Van der Warder's theorem is one of the most important results in Ramsey’s theory, a branch of mathematics that studies the appearance of patterns in objects consisting of a large number of random elements. It all started like this:
In the twenties of the last century, one mathematician faced the following task:
Let the set of all natural numbers be colored in 2 different colors. Is it possible to assert that there is an arbitrarily long arithmetic progression whose numbers are painted in the same color?
 The task seems very simple and a positive solution seems almost obvious. However, attempts to prove this statement did not lead to anything at first. A few years later, the task finally gave in to the young Dutch mathematician Barthel Leendert van der Waerden . He proved a more general version in a slightly different formulation:
The task seems very simple and a positive solution seems almost obvious. However, attempts to prove this statement did not lead to anything at first. A few years later, the task finally gave in to the young Dutch mathematician Barthel Leendert van der Waerden . He proved a more general version in a slightly different formulation:
For any r and k there is a number n (r; k) such that, for any coloring of the set of natural numbers S = {1, 2, ..., n (r; k)} in r different colors, this set S will contain arithmetic a progression of k numbers painted in the same color.
The proof is based on the so-called double induction . A simplified version of this proof can be found, for example, here .
Denote the minimum of the numbers n (r; k) by w (r; k). The numbers w (r; k) are usually called van der Waerden numbers. The proof of the van der Waerden theorem does not give exact values of the numbers w (r; k), only the upper bound. And believe me, this upper limit is huge! It turned out that even for two colors, the estimate for the number w (r; k) grows as a function of Ackermann ! This rating from above gradually improved. The latest result, obtained by Timothy Gowers in 2001, reads as follows:
w (r; k) ≤ 2 2 r 2 2 k + 9 .
The result is a little less scary than the original, but still a little frightening. Still, this boundary is very far from the exact values of w (r; k).
A separate branch of research is the determination of the exact values of the numbers w (r; k) for various r and k. This task is very resource intensive (this is typical of most of the tasks of Ramsey Theory). Wikipedia says that at the moment the exact value of w (r; k) is known only for 7 pairs of numbers r and k.
The answer for w (2; 3) is trivial:
For slightly larger values of w (r, k), the proof usually reduces to the following: the length of the colored chain of numbers n is fixed, after which a Boolean formula is constructed in conjunctive normal form to check that these n numbers can be colored taking into account the constraints r and k, and verifies its feasibility with the help of SAT-Solver. If there is a solution, then the number n + 1 is the lower bound for w (r; k), otherwise the number n should be considered the upper bound for w (r; k).
Given that many SAT solvers are based on the DPLL algorithm, the numbers w (r; k) are searched for using splitting algorithms.
We present a simple method for constructing the desired Boolean formula for the number of colors r = 2. Let's get n variables x i , meaning what color the corresponding numbers are painted in. A value of true will mean the 1st color, false - the second. We need to introduce restrictions so that any arithmetic progression contains both colors. This is done very simply: a disjunction of the form (x a 1 ∨x a 2 ∨ ... x a k ) guarantees the presence of the first color, and a disjunction of the form (¬x a 1 ∨¬x a 2 ∨ ... ∨¬x a k ) - the second . Well and, actually, everything - for each arithmetic progression we build 2 formulas and glue everything that turned out into one big CNF.
An example of a formula for r = 2, k = 3 and n = 9:
(x 1 ∨x 2 ∨x 3 ) ∧ (¬x 1 ∨¬x 2 ∨¬x 3 ) (x 2 ∨x 3 ∨x 4 ) (¬x 2 ∨¬x 3 ∨¬x 4 ) (x 3 ∨x 4 ∨x 5 ) ∧ (¬x 3 ∨¬x 4 ¬x 5 )
(x 4 ∨x 5 ∨x 6 ) ∧ (¬x 4 ∨¬x 5 ∨¬x 6 ) (x 5 ∨x 6 ∨x 7 ) (¬x 5 ∨¬x 6 ∨¬x 7 ) (x 6 ∨x 7 ∨x 8 ) ∧ (¬x 6 ∨¬x 7 ∨¬x 8 )
(x 7 ∨x 8 ∨x 9 ) ∧ (¬x 7 ∨¬x 8 ∨¬x 9 ) (x 1 ∨x 3 ∨x 5 ) (¬x 1 ∨¬x 3 ∨¬x 5 ) (x 2 ∨x 4 ∨x 6 ) ∧ (¬x 2 ∨¬x 4 ¬x 6 )
(x 3 ∨x 5 ∨x 7 ) ∧ (¬x 3 ∨¬x 5 ∨¬x 7 ) (x 4 x 6 ∨x 8 ) (¬x 4 ∨¬x 6 ∨¬x 8 ) (x 5 ∨x 7 ∨x 9 ) ∧ (¬x 5 ∨¬x 7 ∨¬x 9 )
(x 1 ∨x 4 ∨x 7 ) ∧ (¬x 1 ∨¬x 4 ∨¬x 7 ) (x 2 ∨x 5 ∨x 8 ) (¬x 2 ∨¬x 5 ∨¬x 8 ) ∧ (x 3 ∨x 6 ∨x 9 ) ∧ (¬x 3 ∨¬x 6 ∨¬x 9 )
(x 1 ∨x 5 ∨x 9 ) ∧ (¬x 1 ∨¬x 5 ∨¬x 9 )
In the previous spoiler proved that this formula is impossible.
Let us now write our own splitting algorithm for searching for numbers w (2; k), which does not use any tinsel like SAT-solver. We will write in C ++ (I use MS Visual Studio). The basis of the algorithm is as follows:
The dfs procedure is the backbone of the algorithm. The constants N and K (the length of the sequence and the length of the arithmetic progression, respectively) will be inserted into the code by the preprocessor as numbers, sometimes it helps the compiler to better optimize the code. The sets A and B (elements of the sequence painted in the first and second colors, respectively) are specified by a bit mask of length N. Now you should hang the functions on the proposed backbone
The choice function is one of the most interesting:
The strategy for selecting an element, embedded in the choice, is as follows: the element that is included in the largest number of potential monochrome arithmetic progressions is selected. But that’s not all: the more the potential progression of colored numbers, the greater the contribution it makes to the estimate. As a rule, in splitting algorithms, you always need to choose the element that does everything as badly as possible and leads to a conflict (when the check function returns false). Such a strategy often cuts out unnecessary branches, reducing the space of options.
Now consider the check procedure:
This procedure is small, simple and understandable, so it makes no sense to dwell on it.
Finally, the reduce procedure:
We are simply looking for progressions in which all elements except one are painted in one color, and one is not painted. Well, actually, we paint it in the opposite color. The flag variable holds in itself - we painted something on the current pass or not. If not, we exit, otherwise we check for contradictions and if they are not, we go through all the progressions again.
The code was tested on a laptop Core i5 4Gb RAM. With the values of the parameters N = 177 K = 5, the following example was found in 2 minutes:
A and B are colors. A question means that it does not matter to us what kind of color in a given position. That is, in fact, we found as many as 32 examples of length 177, in which there is no monochrome arithmetic progression of length 5.
On the parameters N = 178 K = 5, the code worked for 20.5 minutes and showed that there are no desired arithmetic progressions. Not bad for 2,178 options in general.
This code can be infinitely optimized - select the necessary data structures for quick execution of choice, check and reduce, search for a more optimal strategy for selecting an element for branching, or at least paint the very first selected element in only one color. But this is already beyond the scope of this article.
Of course, the code also works to calculate w (2; 3) and w (2; 4) (the whole thing was initially tested on them).
What can be said about the case of K = 6? More recently (in 2008) it was proved that w (2; 6) = 1132 and this took about 250 days of computing on a cluster of 200 cores. By the way, the implementation of their algorithm proves that w (2; 5) = 178, in less than 3 seconds on one core. For the case K = 7, the question remains open.
PS Not all the links were read deeply, so if any link is really off topic, I’ll remove it.
I will talk about the so-called splitting algorithms (in particular, about the DPLL algorithm), about the theorem and van der Waerden numbers, and in conclusion of the article we will write our own splitting algorithm and in half an hour of calculations we will prove that the number w (2; 5 ) equal to 178 (pioneers in 1978, it took more than 8 days of calculations).
Splitting algorithm
This is a fairly general algorithm that solves the following problem: there is some finite set S and we want to divide it into two subsets A and B, with some properties, or to determine that the set S cannot be divided in the necessary way.
This is done in the following way: 3 non-intersecting subsets A, B, C are supported, which completely cover the set S, where C is the set of those elements that we have not yet distributed between A and B. Initially, C = S, and A and B are empty. At each iteration in the set C, the element a is arbitrarily chosen, which can be placed either in the set A or in the set B. In fact, we do both, and then recursively process both possible options.
')

The result is a splitting tree, the leaves of which contain all sorts of divisions of the set S into A and B, and the set C is empty. Now we just need to check for all leaves that the properties of interest to us.
“Allow me!”, You will say, “than this is better than the obvious brute force of 2 | S | options? And the whole thing in the cutoffs, which are very convenient to add to the above proposed core of the algorithm!
List of cuts:
- If partially constructed A and B do not fit - rollback
- Moving an element from S to A or B may result in moving other elements from S to A or B
- Proper selection of the element a of S at each step can significantly reduce the size of the search tree
With the use of clippings, the size of the tree is greatly reduced, the number of leaves decreases noticeably, sometimes to 0 (this means that it is impossible to divide S into A and B as appropriate). Although the complexity of the algorithm still remains exponential at worst.
It is convenient to explain the general splitting algorithm and all the proposed cut-offs using the example of the classical DPLL algorithm.
DPLL algorithm
The Davis – Putnam – Laugemann – Loveland algorithm (DPLL) was developed in 1962 to determine the feasibility of Boolean formulas written in conjunctive normal form, i.e. to solve the problem of SAT. The algorithm turned out to be so efficient that after more than 50 years it is the basis for the majority of effective SAT solvers.
Let's take a closer look at what the DPLL algorithm does. He takes the Boolean formula and tries to divide all the variables in it into two sets A and B, where A is the set of all variables with a value of true and B is the set of all variables with a value of false.
At each step, a variable is selected in some way, which has not yet been assigned a value (let's call such variables free ) and is assigned the value true (this variable is entered into the set A). After that, the resulting simplified problem is solved. If it is doable, then the original formula is doable. Otherwise, the selected variable is assigned the value false (it is entered in B) and the problem is solved for the new simplified formula. If it is doable, then the original formula is doable. Otherwise - alas, the original formula is impracticable.
After each assignment, the formula is further simplified using the following two rules:
- Variable propagation (unit propagation). If exactly one variable remains in any clause, then it must be assigned such a value so that the clause finally becomes true (move to A or B depending on whether there is a negative or not).
- Elimination of “pure” variables (pure literal elimination). If any variable enters the formula with only negatives, or always without negatives, it is called pure . This variable can be assigned such a value that all its entries will be true, which will reduce the number of free variables.
These two rules should be applied as long as they are applied: usually after the first assignment, a whole cascade of simplifications follows, which well reduces the number of free variables.
If, after simplification, we have received an empty clause (all its simple conjuncts are false) - the current formula is not feasible and should be rolled back. If there are no free variables left, then the formula is feasible and the work of the algorithm can be completed. You can also finish the work of the algorithm if the clause is not left - you can assign unused free variables in an arbitrary way.
A small C-like pseudocode explaining what happens:
bool DPLL( eq F, set A, set B, set C ) { while(1) { // if (F is empty) { // ! write A, B, C; return true; } if (F contains an empty clause) return false; // // bool flag = false; if (unit_propagation(&F, &A, &B, &C)) flag = true; if (pure_literal_elimination(&F, &A, &B, &C)) flag = true; if (!flag) break; // } // x = choose_literal(F, ); if (DPLL(F ∧ (x), A^x, B, C^x)) return true; if (DPLL(F ∧ (¬x), A, B^x, C^x)) return true; return false; } The & symbol shows that in the function unit_propagation and pure_literal_elimination, the variables F, A, B and C are passed by reference, i.e. they can change inside. If anything has changed, these functions return true. When recursive descent - on the contrary, copies of objects are created. The ^ icon excludes an object from the set if it exists or adds if it does not exist.
Consider the following formula and, using its example, let's see how the DPLL algorithm works:
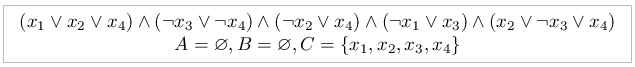
The simplification rules do not apply to this formula, so we will have to branch our tree. As an element for branching, we take x 1 and, for a start, assign it the value true. We get the following chain of simplifications:

Double arrows show that we use the first rule, namely, we find a lonely variable and assign it the desired value.
Unfortunately, this branch leads to an impracticable formula, i.e. In this branch, we tried in vain. We roll back and try to set the variable x 1 to false. This will lead to the following chain of simplifications:

Triple arrows indicate that we apply the second rule of simplification. Success is waiting for us in this branch - 2 solutions were found!
Whole walk tree:

Since the transformations shown by double and triple arrows occur inside each vertex of the tree, it turns out that the tree itself actually consists of only three vertices! However, it was probably possible to come up with a more intricate example.
Note that if, at the very beginning, for the branching, for example, the element x 2 was chosen, then the desired tree would have been much smaller and the answer would have been found much earlier (the necessary calculations are proposed to be made to the reader independently). Therefore, the element selection strategy for branching is very important. For example, you can choose to branch a variable that is included in the largest number of clauses.
It is also worth noting that with the help of this algorithm it is impossible to find all the solutions - this is prevented by the heuristic of the exclusion of “pure” variables. It may well be missing a solution in which the value of the variable that we, following the heuristic, set to true, is false. To search for all solutions, the second rule should be excluded from the algorithm.
Theorem and van der Waerden numbers
Van der Warder's theorem is one of the most important results in Ramsey’s theory, a branch of mathematics that studies the appearance of patterns in objects consisting of a large number of random elements. It all started like this:
In the twenties of the last century, one mathematician faced the following task:
Let the set of all natural numbers be colored in 2 different colors. Is it possible to assert that there is an arbitrarily long arithmetic progression whose numbers are painted in the same color?
 The task seems very simple and a positive solution seems almost obvious. However, attempts to prove this statement did not lead to anything at first. A few years later, the task finally gave in to the young Dutch mathematician Barthel Leendert van der Waerden . He proved a more general version in a slightly different formulation:
The task seems very simple and a positive solution seems almost obvious. However, attempts to prove this statement did not lead to anything at first. A few years later, the task finally gave in to the young Dutch mathematician Barthel Leendert van der Waerden . He proved a more general version in a slightly different formulation:For any r and k there is a number n (r; k) such that, for any coloring of the set of natural numbers S = {1, 2, ..., n (r; k)} in r different colors, this set S will contain arithmetic a progression of k numbers painted in the same color.
The proof is based on the so-called double induction . A simplified version of this proof can be found, for example, here .
Denote the minimum of the numbers n (r; k) by w (r; k). The numbers w (r; k) are usually called van der Waerden numbers. The proof of the van der Waerden theorem does not give exact values of the numbers w (r; k), only the upper bound. And believe me, this upper limit is huge! It turned out that even for two colors, the estimate for the number w (r; k) grows as a function of Ackermann ! This rating from above gradually improved. The latest result, obtained by Timothy Gowers in 2001, reads as follows:
w (r; k) ≤ 2 2 r 2 2 k + 9 .
The result is a little less scary than the original, but still a little frightening. Still, this boundary is very far from the exact values of w (r; k).
A separate branch of research is the determination of the exact values of the numbers w (r; k) for various r and k. This task is very resource intensive (this is typical of most of the tasks of Ramsey Theory). Wikipedia says that at the moment the exact value of w (r; k) is known only for 7 pairs of numbers r and k.
| r / k | 3 | four | five | 6 |
|---|---|---|---|---|
| 2 colors | 9 | 35 | 178 | 1132 |
| 3 colors | 27 | 293 | ||
| 4 colors | 76 |
The answer for w (2; 3) is trivial:
Proof that w (2; 3) = 9
Another proof with a similar idea and in a slightly more detailed form is given here .
An example of painting 8 numbers in 2 colors so that there is no monochromatic arithmetic progression of length 3 among them looks like this:
1 2 3 4 5 6 7 8
This means that w (2; 3)> 8. For 9 colors, let's consider the numbers 4 and 6. Without loss of generality, two cases are possible: either these two numbers are painted in the same color, or different.
1) Let 4 and 6 be colored red:
1 2 3 4 5 6 7 8 9
Then we are obliged to paint 5 in blue, because otherwise there are three red numbers 4 5 6. Similar arguments for 2 and 8. As a result, we get a blue three 2 5 8:
1 2 3 4 5 6 7 8 9
2) Let 4 be blue and 6 be red:
1 2 3 4 5 6 7 8 9
Then, without loss of generality, 5 can be painted blue. It follows from this that 3 should be painted red to avoid blue 3 4 5. Next, 9 should be painted blue to avoid red 3 6 9. Subtotal:
1 2 3 4 5 6 7 8 9
The number 1 should be red to avoid blue 1 5 9. From this follows blue 2, because otherwise we get red 1 2 3. To avoid red 2 5 8, paint 8 in red and eventually we get:
1 2 3 4 5 6 7 8 9
Now, if we paint 7 in red, then we get the red three 6 7 8. If we paint 7 in blue, the blue three will come out 5 7 9.
An example of painting 8 numbers in 2 colors so that there is no monochromatic arithmetic progression of length 3 among them looks like this:
1 2 3 4 5 6 7 8
This means that w (2; 3)> 8. For 9 colors, let's consider the numbers 4 and 6. Without loss of generality, two cases are possible: either these two numbers are painted in the same color, or different.
1) Let 4 and 6 be colored red:
1 2 3 4 5 6 7 8 9
Then we are obliged to paint 5 in blue, because otherwise there are three red numbers 4 5 6. Similar arguments for 2 and 8. As a result, we get a blue three 2 5 8:
1 2 3 4 5 6 7 8 9
2) Let 4 be blue and 6 be red:
1 2 3 4 5 6 7 8 9
Then, without loss of generality, 5 can be painted blue. It follows from this that 3 should be painted red to avoid blue 3 4 5. Next, 9 should be painted blue to avoid red 3 6 9. Subtotal:
1 2 3 4 5 6 7 8 9
The number 1 should be red to avoid blue 1 5 9. From this follows blue 2, because otherwise we get red 1 2 3. To avoid red 2 5 8, paint 8 in red and eventually we get:
1 2 3 4 5 6 7 8 9
Now, if we paint 7 in red, then we get the red three 6 7 8. If we paint 7 in blue, the blue three will come out 5 7 9.
For slightly larger values of w (r, k), the proof usually reduces to the following: the length of the colored chain of numbers n is fixed, after which a Boolean formula is constructed in conjunctive normal form to check that these n numbers can be colored taking into account the constraints r and k, and verifies its feasibility with the help of SAT-Solver. If there is a solution, then the number n + 1 is the lower bound for w (r; k), otherwise the number n should be considered the upper bound for w (r; k).
Given that many SAT solvers are based on the DPLL algorithm, the numbers w (r; k) are searched for using splitting algorithms.
We present a simple method for constructing the desired Boolean formula for the number of colors r = 2. Let's get n variables x i , meaning what color the corresponding numbers are painted in. A value of true will mean the 1st color, false - the second. We need to introduce restrictions so that any arithmetic progression contains both colors. This is done very simply: a disjunction of the form (x a 1 ∨x a 2 ∨ ... x a k ) guarantees the presence of the first color, and a disjunction of the form (¬x a 1 ∨¬x a 2 ∨ ... ∨¬x a k ) - the second . Well and, actually, everything - for each arithmetic progression we build 2 formulas and glue everything that turned out into one big CNF.
An example of a formula for r = 2, k = 3 and n = 9:
(x 1 ∨x 2 ∨x 3 ) ∧ (¬x 1 ∨¬x 2 ∨¬x 3 ) (x 2 ∨x 3 ∨x 4 ) (¬x 2 ∨¬x 3 ∨¬x 4 ) (x 3 ∨x 4 ∨x 5 ) ∧ (¬x 3 ∨¬x 4 ¬x 5 )
(x 4 ∨x 5 ∨x 6 ) ∧ (¬x 4 ∨¬x 5 ∨¬x 6 ) (x 5 ∨x 6 ∨x 7 ) (¬x 5 ∨¬x 6 ∨¬x 7 ) (x 6 ∨x 7 ∨x 8 ) ∧ (¬x 6 ∨¬x 7 ∨¬x 8 )
(x 7 ∨x 8 ∨x 9 ) ∧ (¬x 7 ∨¬x 8 ∨¬x 9 ) (x 1 ∨x 3 ∨x 5 ) (¬x 1 ∨¬x 3 ∨¬x 5 ) (x 2 ∨x 4 ∨x 6 ) ∧ (¬x 2 ∨¬x 4 ¬x 6 )
(x 3 ∨x 5 ∨x 7 ) ∧ (¬x 3 ∨¬x 5 ∨¬x 7 ) (x 4 x 6 ∨x 8 ) (¬x 4 ∨¬x 6 ∨¬x 8 ) (x 5 ∨x 7 ∨x 9 ) ∧ (¬x 5 ∨¬x 7 ∨¬x 9 )
(x 1 ∨x 4 ∨x 7 ) ∧ (¬x 1 ∨¬x 4 ∨¬x 7 ) (x 2 ∨x 5 ∨x 8 ) (¬x 2 ∨¬x 5 ∨¬x 8 ) ∧ (x 3 ∨x 6 ∨x 9 ) ∧ (¬x 3 ∨¬x 6 ∨¬x 9 )
(x 1 ∨x 5 ∨x 9 ) ∧ (¬x 1 ∨¬x 5 ∨¬x 9 )
In the previous spoiler proved that this formula is impossible.
We apply knowledge in practice
Let us now write our own splitting algorithm for searching for numbers w (2; k), which does not use any tinsel like SAT-solver. We will write in C ++ (I use MS Visual Studio). The basis of the algorithm is as follows:
#pragma comment(linker,"/STACK:64000000") #include <iostream> #include <bitset> #include <time.h> #include <memory.h> using namespace std; #define N 178 #define K 5 #define BSET bitset< N > bool dfs( BSET & A, BSET & B ) { int i = choice( A, B ); if (i<0) { for (int a=0; a<N; a++) if (A[a]) cout << "A"; else if (B[a]) cout << "B"; else cout << "?"; cout << "\n"; return true; } A[i] = true; if (check(A, B)) { BSET A1 = A, B1 = B; if (reduce( A1, B1 )) if (dfs( A1, B1 )) return true; } A[i] = false; B[i] = true; if (check( A, B )) { BSET A1 = A, B1 = B; if (reduce( A1, B1 )) if (dfs( A1, B1 )) return true; } B[i] = false; return false; } int main() { freopen("input.txt","r",stdin); freopen("output.txt","w",stdout); BSET A, B; if (!dfs( A, B )) cout << "No counterexamples\n"; cout << "n=" << N << " k=" << K << "\n"; cout << "time=" << clock() << "\n"; return 0; } The dfs procedure is the backbone of the algorithm. The constants N and K (the length of the sequence and the length of the arithmetic progression, respectively) will be inserted into the code by the preprocessor as numbers, sometimes it helps the compiler to better optimize the code. The sets A and B (elements of the sequence painted in the first and second colors, respectively) are specified by a bit mask of length N. Now you should hang the functions on the proposed backbone
- choice - the choice of the element on which we will branch our tree.
- check — Verifies that there is no arithmetic progression in the sequence of length K.
- reduce - painting of additional elements for which the color can be determined uniquely.
The choice function is one of the most interesting:
int cost[N]; int choice( BSET & A, BSET & B ) { memset( cost, 0, sizeof(cost) ); for (int a=0; a<N; a++) for (int d=1; a+d*(K-1)<N; d++) { int cnt1=0, cnt2=0; for (int c=0; c<K; c++) if (A[a+c*d]) cnt1 ++; for (int c=0; c<K; c++) if (B[a+c*d]) cnt2 ++; if (cnt1==0 || cnt2==0) for (int c=0; c<K; c++) if (!A[a+c*d] && !B[a+c*d]) cost[a+c*d] += cnt1+cnt2+1; } int mx = 0; for (int a=0; a<N; a++) mx = max( mx, cost[a] ); if (mx > 0) for (int a=0; a<N; a++) if (cost[a] == mx) return a; return -1; } The strategy for selecting an element, embedded in the choice, is as follows: the element that is included in the largest number of potential monochrome arithmetic progressions is selected. But that’s not all: the more the potential progression of colored numbers, the greater the contribution it makes to the estimate. As a rule, in splitting algorithms, you always need to choose the element that does everything as badly as possible and leads to a conflict (when the check function returns false). Such a strategy often cuts out unnecessary branches, reducing the space of options.
Now consider the check procedure:
bool check( BSET & A, BSET & B ) { for (int a=0; a<N; a++) for (int d=1; a+d*(K-1)<N; d++) { bool f1=true, f2=true; for (int c=0; c<K; c++) f1 &= A[a+c*d]; for (int c=0; c<K; c++) f2 &= B[a+c*d]; if (f1 || f2) return false; } return true; } This procedure is small, simple and understandable, so it makes no sense to dwell on it.
Finally, the reduce procedure:
bool reduce( BSET & A, BSET & B ) { while ( 1 ) { bool flag = false; for (int a=0; a<N; a++) for (int d=1; a+d*(K-1)<N; d++) { int cnt1=0, cnt2=0; for (int c=0; c<K; c++) if (A[a+c*d]) cnt1 ++; for (int c=0; c<K; c++) if (B[a+c*d]) cnt2 ++; if (cnt1+cnt2<K) { if (cnt1 == K-1) for (int c=0; c<K; c++) if (!A[a+c*d]) { B[a+c*d] = true; flag = true; } if (cnt2 == K-1) for (int c=0; c<K; c++) if (!B[a+c*d]) { A[a+c*d] = true; flag = true; } } } if (!flag) break; if (!check( A, B )) return false; } return true; } We are simply looking for progressions in which all elements except one are painted in one color, and one is not painted. Well, actually, we paint it in the opposite color. The flag variable holds in itself - we painted something on the current pass or not. If not, we exit, otherwise we check for contradictions and if they are not, we go through all the progressions again.
results
The code was tested on a laptop Core i5 4Gb RAM. With the values of the parameters N = 177 K = 5, the following example was found in 2 minutes:
BBBABBBBABB?BAAABABBBA?AABAAAABAAAABBBABAAABBBBABBBBABB?BAAABABBBAAAABAAAABAABABBBABAAABA
BBABBBBABBABAAABABBBAAAABAAAABAABABBBABAAABABBABBBBABB?BAAABABBBABAABAAAABAABABBBABAAAB?A and B are colors. A question means that it does not matter to us what kind of color in a given position. That is, in fact, we found as many as 32 examples of length 177, in which there is no monochrome arithmetic progression of length 5.
On the parameters N = 178 K = 5, the code worked for 20.5 minutes and showed that there are no desired arithmetic progressions. Not bad for 2,178 options in general.
This code can be infinitely optimized - select the necessary data structures for quick execution of choice, check and reduce, search for a more optimal strategy for selecting an element for branching, or at least paint the very first selected element in only one color. But this is already beyond the scope of this article.
Of course, the code also works to calculate w (2; 3) and w (2; 4) (the whole thing was initially tested on them).
What can be said about the case of K = 6? More recently (in 2008) it was proved that w (2; 6) = 1132 and this took about 250 days of computing on a cluster of 200 cores. By the way, the implementation of their algorithm proves that w (2; 5) = 178, in less than 3 seconds on one core. For the case K = 7, the question remains open.
Read
- Splitting algorithms on Lectorium (video, lecture slides)
- Bron-Kerbosh search algorithm for all clicks in the graph (in fact, the splitting algorithm)
- DPLL-algorithm on Wikipedia ( rus , eng )
- Van der Waerden theorem and numbers (eng)
- A. Ya. Khinchin. Three Pearls of Number Theory
- Bible Code, Ramsey Theory, and the Existence of God
- Ronald L. Graham, Joel X. Spencer. Ramsey Theory
- RS Stevens, R. Shantaram. Computer-Generated van der Waerden Partitions (eng, pdf)
- Michal Kouril, Jerome L. Paul. The van der Waerden Number W (2,6) Is 1132 (eng, pdf)
PS Not all the links were read deeply, so if any link is really off topic, I’ll remove it.
Source: https://habr.com/ru/post/224069/
All Articles