Game 2048 in Wolfram Mathematica
Translation of the post 2048, Wolfram Style , written for the official blog of Wolfram Research by Dan Fortunato , junior programmer of Wolfram | Alpha Parser Content.
The archive with the Wolfram Mathematica file, which contains the code, you can download here .
')
If during the past few weeks you went online, then you could hardly not meet with a game called 2048 , developed by Gabriel Chirulli. Based on similar games, 1024! from Veewo Studio and THREES from Asher Wallmer, this game has a simple mechanic that will drag you down for a long time - move the chips on which the powers of 2 are written and connect them in pairs to get even higher degrees. The main goal of the game is to get a 2048 chip. It is quite difficult to explain how interesting and exciting this game is in reality, so I recommend that you play it yourself.
To pay tribute to this simple game (and in honor of all math games!), I decided to demonstrate the full power of the Wolfram Language , using it to develop our own version of 2048. Let's start!
The 4x4 matrix, filled with empty elements (rows of zero length) will serve as the main structure for the playing field:
In [1]: =

Out [2] =
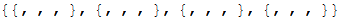
After the start of the new game, I will randomly place two chips on the field with values of 2 or 4. I will give higher priority to chip 2, so it will appear on the field more often.
In [3]: =

In [4]: =

Out [4] =
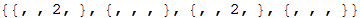
It is time to make our playing field a little more beautiful. I can completely replicate the style of the original game by importing its CSS style (CSS — Cascading Style Sheets, cascading style sheets). As you can see, in CSS I was able to find the colors for the background and the text of all the chips.
In [5]: =

Out [8] =

Now I have a list containing each chip number and its corresponding colors! Next, I can process it by creating a function to search for color and translate it from HEX (hexadecimal color used in CSS) to RGB (a color model based on a combination of red, green, and blue). I also define colors for the rest of the playing field and, just in case, for some colors by default.
In [9]: =

In [10]: =

In [13]: =

Now I use color information to write the function that draws the chips. You need to be careful and make the font size smaller when the number of digits in the number grows.
In [15]: =

In [16]: =

In [17]: =
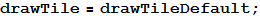
I defined the drawTile function so that it can be easily changed later ...
In [18]: =
Out [18] =
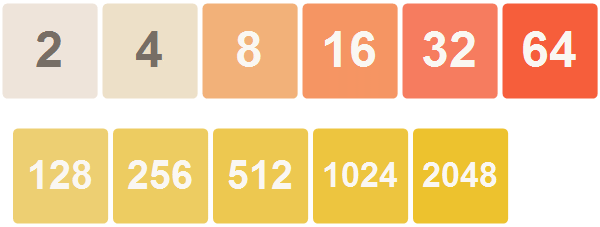
To apply this style to the original playing field, I simply consider each element of the playing field in the matrix and place the corresponding chip in the right place.
In [19]: =

In [20]: =

Out [20] =

Looks beautiful! Now we need to learn how to control the game.
When one of the keys is pressed, I want all the pieces to move along the board in the indicated direction as far as possible, and the same pieces should be combined. I can use the NotebookEventActions option to register keystrokes and respond accordingly. I will make the control be carried out with the wasd keys, you can choose any others:
In [21]: =
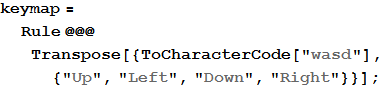
In [22]: =

Now let's think about what happens when the chips move, say, to the left. First of all, I need to implement the union of identical chips. Each line should be considered separately, since with a horizontal offset, vertical matches are not combined. I want to find sequences of two identical numbers, perhaps with empty cells between them, and replace them with the sum. Here the power of the Wolfram Language comes to the rescue, and I can use the mapping to a given patterned expression to make it easy.
In [23]: =
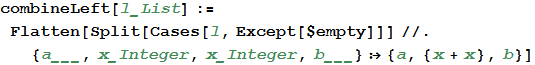
After adding the same chips, all I have to do is add a few empty elements to the right to fill the line. The procedure is repeated for all lines of the playing field.
In [24]: =

The right shift is performed in the same way, with one minor change - I want the combinations of identical chips on the right to unite before the combinations to the left. Consider the string {$ empty, 2, 2, 2} as an example. Using the combineLeft function and clicking the left arrow, I get the string {$ empty, $ empty, 4, 2}, but in fact I want the right pair of twos to first merge. Reversing the line, shifting the cells to the left and reverse flip easily solve the problem.
In [25]: =
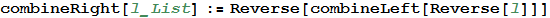
In [26]: =
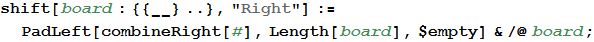
Now that we have these two functions, it’s very easy to shift up and down! A shift up is the same as a left shift in a transposed playing field, followed by reverse transposition. Shifting operations to the right and down are also related.
In [27]: =

If the key is pressed, new chips on the field should be added only if the state of the field has changed, that is, if some of the chips have moved or merged. To do this, you need to track the previous state of the playing field.
Now we will learn how to keep counting points during the game. Every time when two chips are combined, I collect their sum by the Sow function, and then I use the Reap function on all the amounts, when all possible unions are completed. I also derive the value of the highest received at the moment chips.
In [29]: =

Finally, let's add a win and lose test. A game is considered to be won if the largest chip on the field is 2048 or higher. I lost if the board is full and I no longer have possible moves. In this case, I can again use the pattern expression language to determine if possible combinations of chips remain on the board.
In [30]: =

In [31]: =
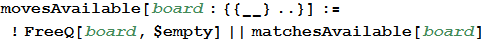
Using the Dynamic function, I can maintain the displayed playing field in full accordance with the changes made. In addition, I can surround this with the DynamicModule function and use Initialization to customize the keystroke processing and the playing field. By placing the DynamicModule inside CreateDialog we can open the game in a separate window.
Finally, the game is completely ready.
In [32]: =


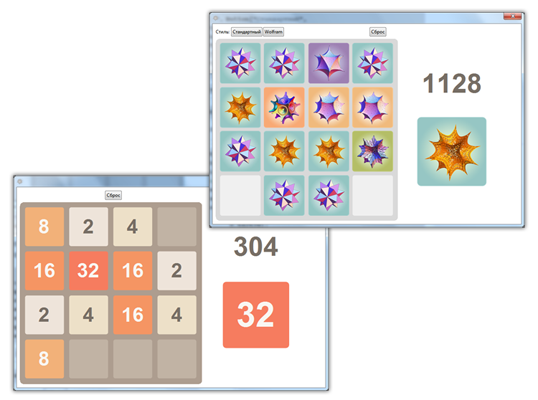
Now everything looks quite nice, but at Wolfram Research we love something more ... pointy. Such as Spikey - logos of different versions of Mathematica and Wolfram | Alpha. Let's change the colors of the chips and their shape.
In [33]: =
In [34]: =
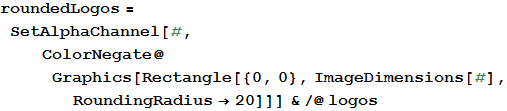
Out [34] =

In [35]: =

In [36]: =
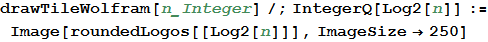
In [37]: =

In [39]: =
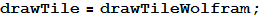
Now we can switch between the two styles with the buttons.
In [40]: =

Out [40] =

In [41]: =

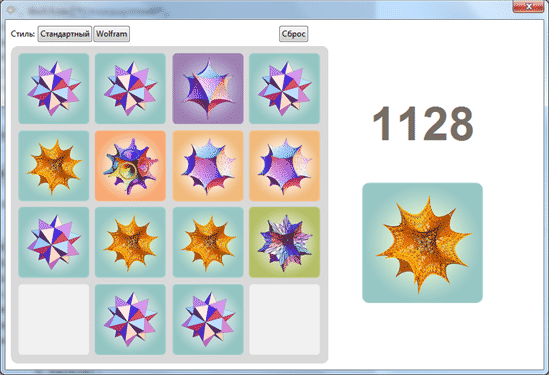
Good luck to you game!
The archive with the Wolfram Mathematica file, which contains the code, you can download here .

')
If during the past few weeks you went online, then you could hardly not meet with a game called 2048 , developed by Gabriel Chirulli. Based on similar games, 1024! from Veewo Studio and THREES from Asher Wallmer, this game has a simple mechanic that will drag you down for a long time - move the chips on which the powers of 2 are written and connect them in pairs to get even higher degrees. The main goal of the game is to get a 2048 chip. It is quite difficult to explain how interesting and exciting this game is in reality, so I recommend that you play it yourself.
To pay tribute to this simple game (and in honor of all math games!), I decided to demonstrate the full power of the Wolfram Language , using it to develop our own version of 2048. Let's start!
The 4x4 matrix, filled with empty elements (rows of zero length) will serve as the main structure for the playing field:
In [1]: =
Out [2] =
After the start of the new game, I will randomly place two chips on the field with values of 2 or 4. I will give higher priority to chip 2, so it will appear on the field more often.
In [3]: =

In [4]: =

Out [4] =
It is time to make our playing field a little more beautiful. I can completely replicate the style of the original game by importing its CSS style (CSS — Cascading Style Sheets, cascading style sheets). As you can see, in CSS I was able to find the colors for the background and the text of all the chips.
In [5]: =

Out [8] =

Now I have a list containing each chip number and its corresponding colors! Next, I can process it by creating a function to search for color and translate it from HEX (hexadecimal color used in CSS) to RGB (a color model based on a combination of red, green, and blue). I also define colors for the rest of the playing field and, just in case, for some colors by default.
In [9]: =

In [10]: =

In [13]: =

Now I use color information to write the function that draws the chips. You need to be careful and make the font size smaller when the number of digits in the number grows.
In [15]: =

In [16]: =

In [17]: =
I defined the drawTile function so that it can be easily changed later ...
In [18]: =
Out [18] =

To apply this style to the original playing field, I simply consider each element of the playing field in the matrix and place the corresponding chip in the right place.
In [19]: =

In [20]: =

Out [20] =

Looks beautiful! Now we need to learn how to control the game.
When one of the keys is pressed, I want all the pieces to move along the board in the indicated direction as far as possible, and the same pieces should be combined. I can use the NotebookEventActions option to register keystrokes and respond accordingly. I will make the control be carried out with the wasd keys, you can choose any others:
In [21]: =

In [22]: =

Now let's think about what happens when the chips move, say, to the left. First of all, I need to implement the union of identical chips. Each line should be considered separately, since with a horizontal offset, vertical matches are not combined. I want to find sequences of two identical numbers, perhaps with empty cells between them, and replace them with the sum. Here the power of the Wolfram Language comes to the rescue, and I can use the mapping to a given patterned expression to make it easy.
In [23]: =
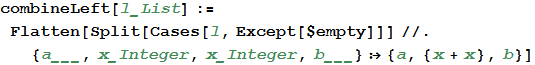
After adding the same chips, all I have to do is add a few empty elements to the right to fill the line. The procedure is repeated for all lines of the playing field.
In [24]: =
The right shift is performed in the same way, with one minor change - I want the combinations of identical chips on the right to unite before the combinations to the left. Consider the string {$ empty, 2, 2, 2} as an example. Using the combineLeft function and clicking the left arrow, I get the string {$ empty, $ empty, 4, 2}, but in fact I want the right pair of twos to first merge. Reversing the line, shifting the cells to the left and reverse flip easily solve the problem.
In [25]: =
In [26]: =
Now that we have these two functions, it’s very easy to shift up and down! A shift up is the same as a left shift in a transposed playing field, followed by reverse transposition. Shifting operations to the right and down are also related.
In [27]: =

If the key is pressed, new chips on the field should be added only if the state of the field has changed, that is, if some of the chips have moved or merged. To do this, you need to track the previous state of the playing field.
Now we will learn how to keep counting points during the game. Every time when two chips are combined, I collect their sum by the Sow function, and then I use the Reap function on all the amounts, when all possible unions are completed. I also derive the value of the highest received at the moment chips.
In [29]: =

Finally, let's add a win and lose test. A game is considered to be won if the largest chip on the field is 2048 or higher. I lost if the board is full and I no longer have possible moves. In this case, I can again use the pattern expression language to determine if possible combinations of chips remain on the board.
In [30]: =

In [31]: =
Using the Dynamic function, I can maintain the displayed playing field in full accordance with the changes made. In addition, I can surround this with the DynamicModule function and use Initialization to customize the keystroke processing and the playing field. By placing the DynamicModule inside CreateDialog we can open the game in a separate window.
Finally, the game is completely ready.
In [32]: =


Now everything looks quite nice, but at Wolfram Research we love something more ... pointy. Such as Spikey - logos of different versions of Mathematica and Wolfram | Alpha. Let's change the colors of the chips and their shape.
In [33]: =

In [34]: =
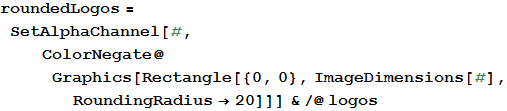
Out [34] =

In [35]: =

In [36]: =
In [37]: =
In [39]: =
Now we can switch between the two styles with the buttons.
In [40]: =

Out [40] =
In [41]: =


Good luck to you game!
Source: https://habr.com/ru/post/223345/
All Articles