For the application in business of imaginary values ​​have already given a premium . Now it's interesting to have something with duals .
A dual number is an extension of the field of real numbers (or any other, for example, complex) of the form a + εb , where a and b are numbers from the original field. In this case, it is assumed that ε ε = 0 .
It turns out that such strange numbers have a practical application.

The main useful property of dual numbers is
f (a + εb) = f (a) + εf '(a) b .
When we have a formula for f (x) , it will not be difficult to get the derivative f '(x) . But often f (x) is available only in the form of an algorithm — for example, as a solution to a specially composed system of linear equations. Running the algorithm with the original data, in which ε is added, we get the result and the value of the derivative with respect to one of the parameters.

A bit of math

Formally, dual numbers form only a ring, not a field — obviously, there are zero divisors among them. But if some “good” problem is solved in real numbers without causing division by 0, then it will also be solved in dual ones. Therefore, in the framework of this article, we neglect mathematical rigor and consider dual numbers as a field.

It is easy to see that the coefficients of ε with each other never multiply together — that is, they can be from an arbitrary module (vector space) over the original field. In this case, we can obtain partial derivatives for several arguments.
')
Prime dual numbers have a matrix representation. 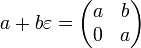. For our generalization, the matrix is ​​transformed into a two-diagonal one, but with further operations it will turn into a triangular one. The coefficients over the second diagonal carry information about the interaction of parameters - in some tasks this may be important information, but for now we will ignore it.
The matrix representation is interesting in that we can, in the problem of linear algebra, “inscribe” instead of the initial number the matrix representation of the dual. I have not researched this approach in depth. I am interested in the case when the number of parameters is comparable to the dimension of the problem, and in this case the complexity of the calculations grows very quickly. The advantage of this approach is the ability to use ready-made high-quality libraries of linear algebra.

Implementation

Unfortunately, the standard libraries based on BLAS and LAPACK work only with real or complex numbers. That's why I started looking for a library written in pure Haskell, a fairly common language in which working with different views is considered normal. But I was disappointed - the only package that works with the Floating type class (it’s not clear why Fractional — the sine cosines in linear algebra are not very necessary) —was linear. And the most interesting operations for me in it are implemented only for matrices of sizes up to 4x4.

For the sake of experiment, I made a simple implementation of dual numbers and a primitive solver of linear equations, which I want to briefly describe.
The source code is posted here .

The data type for representing dual numbers is described as:

data GDual nv = !n :+- (vn) 

Its parameters are the type of representation of the original field and the parameterized container for representing the vector ε. It is implicitly assumed that the container represents the Additive type class from the linear package.

Num's implementation is pretty dumb:

 instance (Eq n, Num n, Additive v) => Num (GDual nv) where fromInteger x = (fromInteger x) :+- zero (x1 :+- y1) + (x2 :+- y2) = (x1 + x2) :+- (y1 ^+^ y2) (x1 :+- y1) - (x2 :+- y2) = (x1 - x2) :+- (y1 ^-^ y2) (x1 :+- y1) * (x2 :+- y2) = (x1 * x2) :+- ((y1 ^* x2) ^+^ (x1 *^ y2)) negate (x :+- y) = (negate x) :+- (y ^* (-1)) abs (a@(x :+- y)) = case (signum x) of 0 -> 0 :+- fmap abs y z -> ((z * x) :+- (x *^ y)) signum (x :+- y) = case (signum x) of 0 -> 0 :+- fmap signum y z -> z :+- zero 

For abs and signum in the neighborhood of zero ( 0: + - ... ), the ratio stated in the type class is violated

 abs x * signum x == x 

But at other points it is preserved.
The implementation of abs is done in such a way that the relation f (a + εb) = f (a) + εf '(a) b is maintained where possible.

Implementing Fractional:

 instance (Num (GDual nv), Fractional n, Additive v) => Fractional (GDual nv) where (x1 :+- y1) / (x2 :+- y2) = (x1 / x2) :+- ((y1 ^/ x2) ^-^ ((x1 / (x2 * x2)) *^ y2)) recip (x :+- y) = (recip x) :+- (y ^/ (x * x)) fromRational x = (fromRational x) :+- zero 

The division is not quite full - it does not know how to divide numbers from the neighborhood of zero even when it is possible (the Additive type class does not provide the necessary functionality for this). But in my field of application of such a division should not be - in the calculations in ordinary numbers in this case happens the division of 0/0.

The implementation of Floating, which for some reason wanted to linear, stupid and bring it, I will not.
Another GDual implements the liler class Epsilon with the nearZero method.

 Math.GDual.Demo.SimpleSparseSolver.solve :: (Fractional t1, Ord t, Epsilon t1) => [[(t, t1)]] -> [[(t, t1)]] 

solves a system of linear equations, which is represented by a rectangular sparse matrix. The matrix is ​​a concatenation of the matrix of coefficients and the column of the right side. solve elementary operations leads the matrix to the unit - the right side turns into an answer.

Remarks

The derivative of the function indicates the sensitivity of the function value to changes or errors in the parameters. But at the same time, rounding errors are not taken into account in the process of calculating the function. These errors can be taken into account by another generalization of numbers: interval arithmetic