Simple pseudo-random selection algorithm

In this post I want to talk about a simple suggestion algorithm based on the choices made earlier. To do this, first of all, set two tasks:

1. Select a random value from the array
2. Select a random value from the array based on the weight of the values.

Certainly, many will notice that ready-made functions exist in many PLs for solving the first problem. However, I will invent a bicycle to solve it differently, for a gradual approach to solving the second task.

For the solution I will use pseudocode, something similar to Javascript. Therefore, my random () method will return a value from 0 to 1.

So, task 1

You can simply iterate through the array in each iteration, randomly receiving true / false, you can use a common Javascript solution of the form Math.floor(Math.random() * maxNumber) , which, by the way, is the abbreviated version of the solution that I will use.
')

Decision

We divide the interval of numbers from 0 to 1 into equal n segments and take the nearest previous value from random :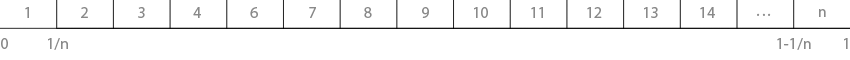

Practical part

For simplicity, let's take an array of 150 elements containing only its own indices. That is, a numerical range from 0 to 150.

 maxNumber = 150; //      elementPart = 100 / maxNumber / 100; //     ,     0.66% randomResult = random(); cursor = 0; for (i = 0; i <= maxNumber; i++) { cursor += elementPart; if (cursor >= randomResult) { result = i; break; } } 

Task 2

Let's enter some initial data:

 items = [ {id: 1, score: 4}, {id: 2, score: 0}, {id: 3} ] 

Where score is a certain value (number of points), which changes the "weight" of the value in front of other values. Points can be awarded for choosing a value or for the similarity of this value with the value selected once. The rules for scoring are limited only by fantasy and the specific application situation.
The attentive reader has noticed that 0 points is not the default value. This is done in order to be able to exclude the value from the sample, because the number of points by default is taken as 1. To do this, we correct the source data:

 for (i = 0; i < items.length; i++) { item = items[i]; if (item.score === 0) { item.remove(); //     continue; } if (item.score === null) { item.score = 1; //  score ,    1 } } 

Decision

The essence of the solution is to change the segments of values ​​in the range from 0 to 1.
Example:

Practical part

Add a weight calculation value:

 sumScores = 0; for (i = 0; i < items.length; i++) { //     sumScores += items[i].score; } for (i = 0; i < items.length; i++) { weight = items[i].score / sumScores; items[i].weight = weight; } 

Here weight is the percentage of the sum of the points of all the elements.
We calculate the sum of the weights and decorate the solution to problem 1:

 sumWeights = 0 for (i = 0; i < items.length; i++) { //     sumWeights += items[i].weight; } cursor = 0; for (i = 0; i < items.length; i++) { cursor += items[i].weight / sumWeights; if (cursor >= randomResult) { suggestedItem = items[i]; break; } } 

Thus, we obtain a value with id = 1 with a higher probability than with id = 3. However, in this case, we will sooner or later come to the fact that the same values ​​will be offered (subject to an increase in the number of points and unless, of course, artificially exclude them from the sample).
This solution is quite applicable to systems where the user needs to offer something most similar - just make a score of the desired values ​​to your liking (same color, same type, maybe the same manufacturer) without forgetting to exclude the selected value by setting the score to 0 .
If you need a set, you are less likely to show such products (for example, why would a person need a second vacuum cleaner, if he just bought it?) Or offer to try something new without discarding the purchased item from the sample (for example, ordering food or consumables ( aroma of electronic cigarettes, etc.)), then you need to make small adjustments to the calculation of the scales:

 for (i = 0; i < items.length; i++) { weight = 1 - items[i].score / sumScore; if (items[i].score == sumScore) { weight = 1; } items[i].weight = weight; } 

Where weight is the inverted value to percentage.
In case if we have only one item in the list, we have a non-zero account, check and assign 1 weight to this item.

Now, adding to the score point every time the choice of this value is made, we move it further (without excluding from the sample), offering alternative options to the user.
These two approaches can be combined: for example, we offer the user of the manufacturer, whose goods he usually buys, but at the same time we offer goods that he has not yet purchased.

A demo can be tried here.

On this topic

You can read about the multi-criteria choice of alternatives and the fuzzy choice rules here .