It was a cold winter of 2063 ... You, sitting in a hut in the Siberian steppes, sipping hot tea, got your favorite vintage smartphone of 2014 sample with the support of GLONASS out of nostalgic reasons - but for some reason he did not find a single satellite. Suddenly, the piercing bell of a red government phone cut the silence - the voice on that side chattering: it turned out that all the GLONASS satellites were out of order due to an unknown failure ... (TZCH? Bookmarks? Who will now disassemble ....)



Well, the hope is now only for you - you need as soon as possible (by Monday) to develop a new satellite navigation system taking into account the achievements of science and technology in 2063: due to the fact that fusion reactors and annihilation engines have become compact enough to fit on aboard the satellite - they are now fixed at one point in near-Earth space, there is no longer any orbit. Accordingly, the almanac and ephemeris (parameters of the orbits of satellites) no longer need to be transmitted from satellite to earth.

The principle of operation of GLONASS in 2063

It happens on a two-dimensional plane. It is known in advance that the receiver is guaranteed not farther than 6378 km from the origin. Satellites are fixed at points remote from the center of coordinates at a distance from 10 thousand to 20 thousand km. Each satellite transmits the same pseudo-random sequence with a transmission rate of 1 megabit (one million bits per second); we receive a signal at a frequency of 10 million samples per second. Since Each satellite transmits a signal at its own frequency - we can receive them independently.

')

A pseudo-random sequence repeats every second. The beginning of a satellite transmitting a pseudo-random sequence and receiving a signal on the ground - ideally coincide, however, due to the fact that the distance from the satellites to the receiver is different - due to the speed of light we receive a signal with a delay (speed of light = 299792458 meters per second) - t. e. first we take the "tail" of the previous sequence, then the "head" of the current one. By calculating the delay of the code sequence - we can estimate the distance to the satellite. Knowing the distance to several satellites - we can roughly determine the coordinates.



Schematically, it will look like this: The radius of the circle drawn is the calculated signal delay multiplied by the speed of light.





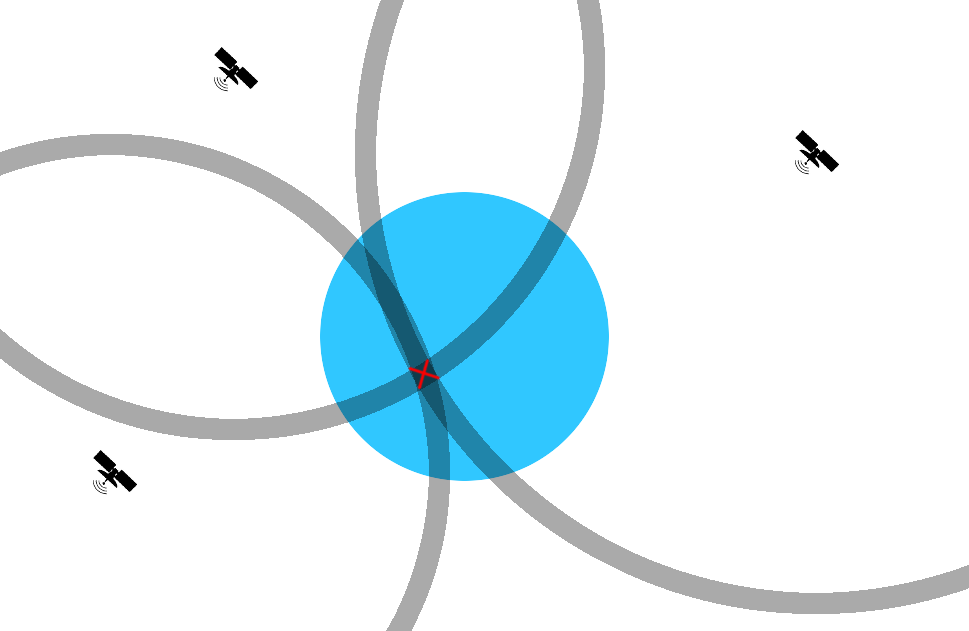
The satellites and the receiver are in place - there is no Doppler shift, and relativistic effects (including gravitational) should not be taken into account. Those. There are no tricks here.

Input Format

Data is entered via standard input.

The first line - the number N from 2 to 255: the number of satellites

Further description of N satellites: in separate lines - coordinates X and Y of the satellite in meters, relative to the origin.

Next - 10 million digits 0 or 1, adopted on the ground pseudo-random sequence from this satellite.



The algorithm for generating a pseudo-random sequence (it is always the same):

data = md5("3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446"+to_string(pos)) 

Where pos is changed from 0 to 999999. If the first character is data> '7', then one is transmitted, otherwise zero.



The receiver receives a signal with a sample 10 times more often, because 0 and 1 are repeated for 10 consecutive samples. More frequent sampling on the receiver allows you to more accurately determine the propagation delay.



Example output: (accepted code sequence shown partially)

 2
 -6.83616e + 006
 1.6126e + 007
 0000000000000000111111111100000000000000000000000000000000 [...]
 -1.07643e + 007
 -1.48409e + 007
 1000000000011111111110000000000111111111111111111111111111111111111 [...]

Output format

Results are printed to standard output.

The real coordinates of the receiver, separated by a space - X and Y, in meters, relative to the origin.



If it is impossible to calculate the coordinates unambiguously, it is acceptable to derive any of the solutions.



Example output:

  -1.81683e + 006 -1.74334e + 006 

Examples of input / output files - you can download it here: s.14.by/glonass-contest.zip

Evaluation of results

If delta is an error in determining the coordinates in meters and T is the time spent on the calculation, then the number of points is calculated using the formula 100 / (delta + 10) + 10 / (T + 1). If the operating time is more than 5 seconds on the i7-3820 processor with HT or the coordinate determination error exceeds 100 1000 meters, then the result does not count. The scores for all tests are summarized.

Programming language

Only Java SE 7 is allowed, third-party libraries cannot be used. The solution should be in one file, no larger than 20kB. You cannot work with the network, access any files on the local machine, work with native code (JNI and co).

Decision making, deadlines and where to send

Decisions are made until 11:59 PM (Moscow time) on May 11 at contest@14.by, the decision file must be attached to the letter - no need to paste the code into the letter itself!



The first line of the decision should contain a comment like:

 //@BarsMonster 

Where BarsMonster is your username on HabraHabr (users can participate and read-only, register )

Prizes

First place in points - 2 BTC,

the second is 1 BTC,

the third is 0.5 BTC.



Additional nomination:

For the most compact solution, passing all the tests (in time and the required accuracy) 1 BTC.



The results will be published on Habré on Monday-Tuesday, the winners with read-only accounts will be invited to Habr, and of course we will try to invite the winners for an interview.

Afterword

Blowing the dust from the shelf of the cabinet you got an ancient folder signed by “GLONASS: reference implementation”, probably containing the implementation of the receiver in one of the ancient programming languages ​​... Maybe after some time you will manage to figure out what is written there ...



Stay tuned for updates and good luck to all!



Update 05/10/2014 2:03 : Corrected description of the code sequence. Will be executed on 64-bit Java (-Xms10g -Xmx30g). Translations of strings are not documented, it is better not to lay it out.

Update 05/10/2014 10:23 : The data will be guaranteed in the disk cache to test the solution, not the disk (I already know its speed, 500 MB / s).

Update 05/10/2014 13:18 : The rounding of the coordinates of satellites creates too many ambiguities. The accuracy of satellite coordinates is guaranteed to 1 mm (3 decimal places in meters). Download the new file - the 3rd test is added to it with high accuracy. All tests for final testing are regenerated with high accuracy.

Update 05/11/2014 6:00 PM : Finally, the text recognition results of the program came. It turned out that it was written in some ancient programming language with a strange name - Erener. It seems the authors really liked the ancient money. Judging by the notes in the fields - the speed and accuracy of work left much to be desired.



Update 05/11/2014 20:11 : Time inexorably comes to an end - the flow of decisions is becoming more turbulent. Results will be published no later than Tuesday. The time of receiving the latest decisions will be traced by a ruthless robot.

Update 05/14/2014 23:22 : Results are published.