Hacker Battles: Parsing PHDays CTF and CTF Quals
Positive Hack Days CTF is an international competition for the protection of information, which is held according to the gaming principle of Capture the Flag. Several teams for a predetermined time to protect their networks and attack others. The main task of the participants is to identify vulnerabilities in the systems of opponents and gain access to secret information (flags), while detecting and eliminating similar vulnerabilities in their system.
In today's topic, we will present an analysis of some interesting tasks faced by participants in past competitions.
This year PHDays CTF will be held for the fourth time. For the first time, the competitions were held during the Positive Hack Days forum in 2011, then the participants of the American PPP team became winners, the next year the Russian team Leet More won, and Eindbazen from Holland became the PHDays III champions. Every year teams from around the world take part in PHDays CTF - from the USA to Japan.
')
More than 600 teams registered to participate in the qualifying competitions this year.

Traditionally, game tasks and infrastructure are prepared in accordance with the legend of the competition - a special storyline that turns a simple set of PHDays CTF tasks into an exciting competition that has a goal. For example, last year, participants saved the fictional world D'Errorim from death. Upcoming competitions will continue this story .
Competition tasks, as a rule, are based on real prototypes: vulnerabilities inherent in CTF tasks and services can be found in various systems in real life. PHDays CTF competitions are also interesting for original game mechanics, which make it possible to implement different and different strategies for playing a game (for more information, see PHDays website ).
Usually, the organizers are preparing for the team unusual tasks not directly related to burglary. For example, during PHDays 2012 additional points could be earned by finding bonus flags in a special container with rubbish, and during PHDays III, the teams had to overcome the “ hacker maze ” - the obstacle course with a laser field, tracking sensors, secret doors, a room with bugs and other interesting tests.
But the main points, of course, are earned exclusively in the course of solving various problems of information security. Let's take a look at some of them.
The qualifying stage of the competition (PHDays CTF Quals) refers to the type of task-based CTF, that is, teams must solve tasks and get points for them. Assignments may fall into one of the following categories:
Let's start with the last category.
PHDays IV CTF Quals participants in one of the tasks needed to decrypt the message hidden in the mp3-file .
As a rule, if the problem statement mentions extracting a message hidden in some container, one of the ready-made solutions from the field of steganography is used. At the same time, in order to find the answer, it is usually necessary to select a program for decryption and run it with the correct keys. That is, the "key to success" in solving a specific task lies in finding a suitable option, previously written by the authors.
In our case, everything is different. If you open the proposed file in a text editor, it looks like this:
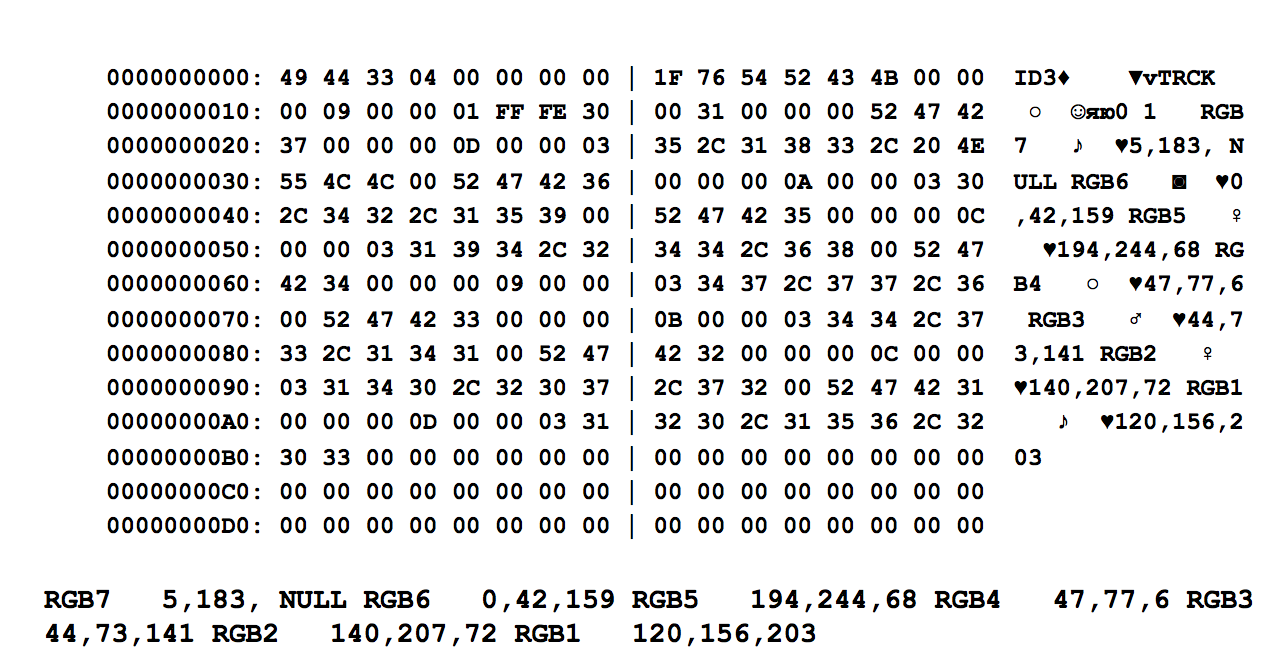
At the beginning of the file are metadata in ID3 format. First comes the TRCK (track number) tag, and then some pieces of text:
RGB7 5.183, NULL RGB6 0.42.159 RGB5 194.244.68 RGB4 47.77.6 RGB3 44.73.141 RGB2 140.207.72 RGB1 120,156,203
This information can be broken down into seven entries (from RGB7 to RGB1):
RGB7 5.183, NULL
RGB6 0.42,159
RGB5 194,244,68
RGB4 47,77,6
RGB3 44,73,141
RGB2 140,207,72
RGB1 120,156,203
After each of the RGB identifiers there are three values. These are usually numbers, but in one case NULL. It is easy to assume that this is an array of records, each of which contains up to three single-byte values. You can sort, combine, turn decimal codes into symbols and display them in hexadecimal, for example, using the following program:
As a result, we get:
The hexadecimal sequence starts with bytes with codes 0x78 0x9C, and this tells us that the zlib data compression algorithm is used. If you use zlib in compression mode with default parameters, the output sequence will start from these bytes.
With a single call to the zlib library's decompress function in Python, you can unpack a packed message:
And then the text will be displayed:
i_hate_ucucuga
It was this flag that had to be sent to the organizers of the competition.
This task belongs to the category of Crypto. According to legend, the session was intercepted, and the teams need to decrypt the transmitted messages.
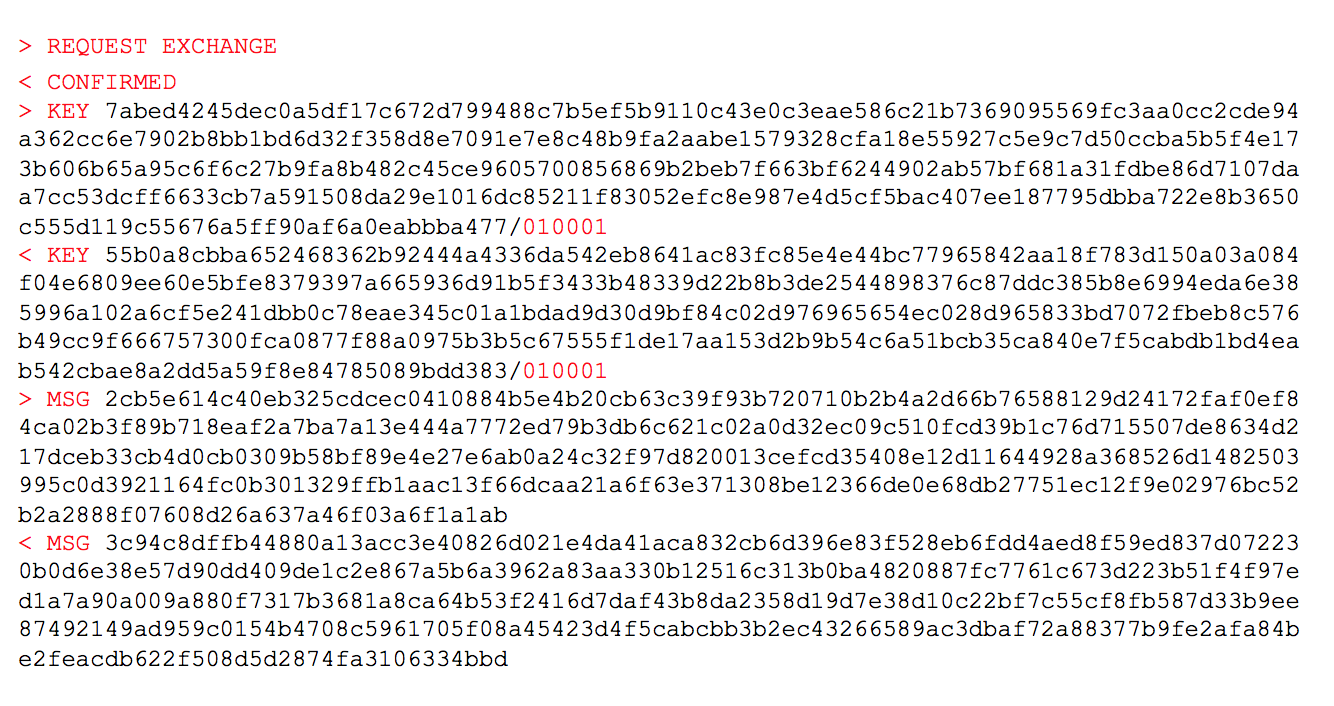
First of all, the process of key exchange is clearly visible, and then the transfer of encrypted data. It is necessary to understand on the basis of which cryptographic basis such communication can be built.
The task is called mars, we can assume that this means Modified RSA.
Each key consists of two parts, and the second part in both cases is 0x010001 == 65537 - the frequently used public exponent RSA (e). This means that in a communication session, the public keys are first exchanged (n 1 / e 1 , n 2 / e 2 ), and then the messages encrypted on them (c1, c2) are exchanged.
If it really is something like RSA, then ci = pow (m i , e i , n i ). It is required to find m 1 and m 2 .
pow is a function of modular exponentiation, pow (val, exp, modulus) == val exp % modulus.
According to the RSA algorithm:
In the task n 1 and n 2 have a length of 1535 bits, that is, they are not amenable to factorization (decomposition into simple factors).
Let's use the implementation of the advanced Euclidean algorithm in Python:
Find the GCD (the greatest common factor) of the numbers n 1 and n 2 :
GCD (n 1 , n 2 ) is 1024 bits long. Find the other dividers of the numbers n 1 and n 2 :
p 1 and p 2 are prime numbers 512 bits long, gcd is a composite number 1024 bits long (most likely 512 * 512), and it is also too large to factor ...
Consider the case when the desired messages m i can be represented by numbers not exceeding p i .
Let n i = p i * q * r, then for 0 <m i <p i the following expression will be true:
pow (m i , e i , n i )% p i == pow (m i , e i , p i )
Then the exponent to decrypt d ' i must satisfy the following expression:
e i * d ' i ≡ 1 mod φ (p i )
The value of d ' i can be found by computing the algebraic complement:
d ' i = invmod (e i , φ (p i ))
For a simple p i true:
φ (p i ) == p i-1 ,
Consequently:
d ' i = invmod (e i , p i-1 )
The calculation of an algebraic complement is implemented by the following function in Python:
You also need a function that turns a number into a string and leaves only the text from the last '\ 0' character to the end of the line:
Calculate di, perform decryption:
And we get the result:
REQUEST: GET_FLAG (SIGNATURE: 5e2d5e0323591b1c).
RESPONSE: its_n0t_ab0ut_p4dd1ng
The flag is the string "
It is given: the source.tar.gz archive containing the ecc.py and task.py files, which contain the key verification scheme implemented using elliptical cryptography. It is known that by connecting to 1955.133.87.171 on port 5555, you can connect to some server:
Since the source code is given, it is worth starting with their analysis. You can even run them.
Since I did not have the libnum module, I had to write it myself. It is sufficient to implement the previously mentioned modular inversion function and the Euclidean algorithm it uses:
So, the
A string is read, SHA-1 from which must be equal to the specified value (“secch4l *”).
Then a random 8-byte prefix is sent to the client. Bytes are encoded as a hex string. In response, the client must send a string no longer than 16 bytes, so that it begins with the specified prefix, and the first 3 bytes of the SHA-1 value from this string must be zero. If all stages are completed successfully, the goflag () function is called.
The following code fragment connects to the server, sends the password, receives the prefix, calculates and sends the response:
After executing this code on the client side, the server performs the goflag () function, which displays something like the following:
EC PASSWORD CHECK
R = 572115218124168948525078362547166172445820217705568707355669424304224832114
SHARED SECRET = R ^ PASSWORD
ENCRYPTED MESSAGE: 7a93846a011e0d0382e94f32d705239e6298169dcec20da5d6
What happens in the
Asymmetric cryptography on elliptic curves is used. The P-256 curve recommended by NIST is selected. The implementation of operations on the curve points does not contain obvious vulnerabilities.
We know the value of R, but without knowing the value of PASSWORD (which is read by the server from the file password.txt) we cannot calculate S. Knowing S would allow us to easily calculate the key. So can encryption be implemented with an error?
The
The code shows that the encrypted message is preceded by a random 8-byte initialization vector iv, and encryption is performed as the XOR flag with a gamma generated as the output of two SHA-256 calculations. Without knowing the value of key, getting a gamma is not possible. But how does the key get in the program?
Derive function from task.py:
It turns out that the value of the point S (consisting of two coordinates - x and y) is used as input SHA-256. In fact, the value of str (int (x * 1024 / y)) is fed to the input of the hash. Since x and y have similar values (these are large integers), the result of arithmetic operations should be close to 1024 (although it may exceed it by several times).
Thus, due to the implementation characteristics of the derive function, the key value can take on a very small number of states. You can simply sort through them all, try to decipher the message on each key, and if it consists only of typed characters - we have achieved success.
Thus, the flag is the line "ecc_is_too_s3cure".
Reverse engineering is another popular job category. In addition to CTF, there is a Best Reverser contest in the PHDays competition program.
The task Shadelt900, as well as the previous three, was part of the PHDays IV CTF Quals program, which took place in January 2014. Commands had to decrypt an image called 'derrorim_enc.bmp'. The means used to encrypt it was known - it is called Shadelt9000.exe, but the decryptor could not be found. Here is this image:

A closer look at the Shadelt9000.exe file makes it clear that the application uses OpenGL. Also there is a copyright inflate 1.2.8 Copyright 1995-2013 Mark Adler, indicating that the program uses the popular compression library zlib.
If you can see in the disassembler where the calls to the zlib functions come from, you can quickly find such a piece of code:

At addresses 0x47F660 and 0x47F7B8 are located data arrays, packed zlib. Unpack them:
After unpacking, the 1.txt file contains a pixel shader:
File 2.txt contains the vertex shader:
The main information about the pixel shader is highlighted in red:

The variable t is the current element of the processed texture (input file),
and in variable g, the current gamma element (generated in a pseudo-random fashion).
In the variable s, we see some value used later for the cyclic shift s.
The output value is actually calculated as
And if you run the program several times with the same input file, then for each element the value of g will change from launch to launch, and t and s will remain the same.
Find how gamma is generated:
It can be seen that it depends on the current time.
From the source archive you can find out that the file derrorim_enc.bmp was created on January 21, 2014 at 18:37:52.
We get the value that the time () function would return at that moment:
0x52de8640
Now copy the file ShadeIt9000.exe to ShadeIt9000_f.exe and fix it.
At offset 00015557 need bytes
replaced by
This is equivalent to replacing
Thus, we have received a version of ShadeIt9000_f, which will always encrypt with the same gamma that was at the time of encryption of the file of interest.
Now you need to prepare values that will help decipher the image:
In the file 00_enc.bmp will be the result of encoding the image, consisting of zero bytes. This will be the gamma in its purest form.
The XX_enc.bmp file will contain the result of encoding the image, consisting of bytes with value 2. This will help us know how many bits each byte cyclically shifted.
Finally, decoding Shadelt9000:
we get:

Above was described the correct, but not the most effective way to solve a task. There is a shorter way.
Immediately behind the vertex shader at addresses 0x47F848 and 0x47F9A0 lies the packed zlib code of the pixel and vertex shader to perform the inverse transform. Perhaps he was accidentally forgotten by the developer of the task. And maybe left intentionally.
The vertex shader codes for encryption and decryption are identical, so there is no point in touching them. And what happens if you replace the pixel shader?
Copy ShadeIt9000_f.exe to ShadeIt9000_d.exe and fix it:
Then run ShadeIt9000_d.exe derrorim_enc.bmp. And we get the decrypted file derrorim_enc_enc.bmp, which (with the exception of small artifacts) is the same as the one we decrypted with the Python script.
That's all for today! Thank you all for your attention, we will be happy to answer questions in the comments.
We remind you that the PHDays IV CTF final will take place on May 21 and 22 during the Positive Hack Days forum. It will be possible to follow the course of the competition not only directly on the court, but also with the help of mobile applications. Follow the news !
See also:
We remind you that registration has already begun for participation in online contests HashRunner and “ Competitive Intelligence ” on PHDays IV!
PS An archive of all PHDays CTF and CTF Quals assignments can be found on the PHDays website . So, if you want to test yourself - go ahead!
PPS A detailed analysis of the tasks presented in the topic was held on a special webinar, which was moderated by Dmitry Sklyarov. Record of the webinar is available at the link: http://my.webinar.ru/record/290241/ .
In today's topic, we will present an analysis of some interesting tasks faced by participants in past competitions.
History and geography
This year PHDays CTF will be held for the fourth time. For the first time, the competitions were held during the Positive Hack Days forum in 2011, then the participants of the American PPP team became winners, the next year the Russian team Leet More won, and Eindbazen from Holland became the PHDays III champions. Every year teams from around the world take part in PHDays CTF - from the USA to Japan.
')
More than 600 teams registered to participate in the qualifying competitions this year.

Tasks and Atmosphere
Traditionally, game tasks and infrastructure are prepared in accordance with the legend of the competition - a special storyline that turns a simple set of PHDays CTF tasks into an exciting competition that has a goal. For example, last year, participants saved the fictional world D'Errorim from death. Upcoming competitions will continue this story .
Competition tasks, as a rule, are based on real prototypes: vulnerabilities inherent in CTF tasks and services can be found in various systems in real life. PHDays CTF competitions are also interesting for original game mechanics, which make it possible to implement different and different strategies for playing a game (for more information, see PHDays website ).
Usually, the organizers are preparing for the team unusual tasks not directly related to burglary. For example, during PHDays 2012 additional points could be earned by finding bonus flags in a special container with rubbish, and during PHDays III, the teams had to overcome the “ hacker maze ” - the obstacle course with a laser field, tracking sensors, secret doors, a room with bugs and other interesting tests.
But the main points, of course, are earned exclusively in the course of solving various problems of information security. Let's take a look at some of them.
Parsing
The qualifying stage of the competition (PHDays CTF Quals) refers to the type of task-based CTF, that is, teams must solve tasks and get points for them. Assignments may fall into one of the following categories:
- Forensic - computer forensics,
- Reverse (reverse engineering) - binary code analysis,
- Pwn - exploitation of vulnerabilities,
- Admin - administration skills,
- Network - knowledge of network infrastructure and protocols
- Crypto - cryptography,
- Stegano - steganography,
- PPC (professional programming and coding) - Olympiad programming,
- Web - search and exploit web vulnerabilities,
- Misc - different.
Let's start with the last category.
Non-obvious tasks
PHDays IV CTF Quals participants in one of the tasks needed to decrypt the message hidden in the mp3-file .
As a rule, if the problem statement mentions extracting a message hidden in some container, one of the ready-made solutions from the field of steganography is used. At the same time, in order to find the answer, it is usually necessary to select a program for decryption and run it with the correct keys. That is, the "key to success" in solving a specific task lies in finding a suitable option, previously written by the authors.
In our case, everything is different. If you open the proposed file in a text editor, it looks like this:

At the beginning of the file are metadata in ID3 format. First comes the TRCK (track number) tag, and then some pieces of text:
RGB7 5.183, NULL RGB6 0.42.159 RGB5 194.244.68 RGB4 47.77.6 RGB3 44.73.141 RGB2 140.207.72 RGB1 120,156,203
This information can be broken down into seven entries (from RGB7 to RGB1):
RGB7 5.183, NULL
RGB6 0.42,159
RGB5 194,244,68
RGB4 47,77,6
RGB3 44,73,141
RGB2 140,207,72
RGB1 120,156,203
After each of the RGB identifiers there are three values. These are usually numbers, but in one case NULL. It is easy to assume that this is an array of records, each of which contains up to three single-byte values. You can sort, combine, turn decimal codes into symbols and display them in hexadecimal, for example, using the following program:
>>> a = [120,156,203, 140,207,72, 44,73,141, 47,77,6, 194,244,68, 0,42,159, 5,183]>>> print "".join(map(chr, a)).encode("hex")As a result, we get:
789ccb8ccf482c498d2f4d06c2f444002a9f05b7The hexadecimal sequence starts with bytes with codes 0x78 0x9C, and this tells us that the zlib data compression algorithm is used. If you use zlib in compression mode with default parameters, the output sequence will start from these bytes.
With a single call to the zlib library's decompress function in Python, you can unpack a packed message:
>>> import zlib >>> print zlib.decompress("".join(map(chr, a))) And then the text will be displayed:
i_hate_ucucuga
It was this flag that had to be sent to the organizers of the competition.
Incorrect cryptography
This task belongs to the category of Crypto. According to legend, the session was intercepted, and the teams need to decrypt the transmitted messages.

First of all, the process of key exchange is clearly visible, and then the transfer of encrypted data. It is necessary to understand on the basis of which cryptographic basis such communication can be built.
The task is called mars, we can assume that this means Modified RSA.
Each key consists of two parts, and the second part in both cases is 0x010001 == 65537 - the frequently used public exponent RSA (e). This means that in a communication session, the public keys are first exchanged (n 1 / e 1 , n 2 / e 2 ), and then the messages encrypted on them (c1, c2) are exchanged.
If it really is something like RSA, then ci = pow (m i , e i , n i ). It is required to find m 1 and m 2 .
pow is a function of modular exponentiation, pow (val, exp, modulus) == val exp % modulus.
According to the RSA algorithm:
- m i = pow (c i , d i , n i ),
- d i * e i ≡ 1 mod φ (n i ),
- n i - the product of several prime numbers
- φ (n) is the Euler function, the number of positive integers with n and less than n.
In the task n 1 and n 2 have a length of 1535 bits, that is, they are not amenable to factorization (decomposition into simple factors).
Let's use the implementation of the advanced Euclidean algorithm in Python:
def egcd(a, b): # Extended Greatest Common Divisor if a == 0: return (b, 0, 1) else: g, y, x = egcd (b % a, a) return (g, x - (b // a) * y, y) Find the GCD (the greatest common factor) of the numbers n 1 and n 2 :
gcd = egcd(n1,n2)[0] GCD (n 1 , n 2 ) is 1024 bits long. Find the other dividers of the numbers n 1 and n 2 :
p1 = n1 / gcd p2 = n2 / gcd p 1 and p 2 are prime numbers 512 bits long, gcd is a composite number 1024 bits long (most likely 512 * 512), and it is also too large to factor ...
Consider the case when the desired messages m i can be represented by numbers not exceeding p i .
Let n i = p i * q * r, then for 0 <m i <p i the following expression will be true:
pow (m i , e i , n i )% p i == pow (m i , e i , p i )
Then the exponent to decrypt d ' i must satisfy the following expression:
e i * d ' i ≡ 1 mod φ (p i )
The value of d ' i can be found by computing the algebraic complement:
d ' i = invmod (e i , φ (p i ))
For a simple p i true:
φ (p i ) == p i-1 ,
Consequently:
d ' i = invmod (e i , p i-1 )
The calculation of an algebraic complement is implemented by the following function in Python:
def invmod(a, m): # Modular inversion g, x, y = egcd (a, m) if g == 1: return x % m raise Exception("modular inverse does not exist") You also need a function that turns a number into a string and leaves only the text from the last '\ 0' character to the end of the line:
def showX(v): print ("%0256X" % v).decode("hex").split('\0')[-1] Calculate di, perform decryption:
d1 = invmod(e, p1-1) d2 = invmod(e, p2-1) showX(pow(c1, d1, p1)) showX(pow(c2, d2, p2)) And we get the result:
REQUEST: GET_FLAG (SIGNATURE: 5e2d5e0323591b1c).
RESPONSE: its_n0t_ab0ut_p4dd1ng
The flag is the string "
its_n0t_ab0ut_p4dd1ng ".Cryptographic task secc
It is given: the source.tar.gz archive containing the ecc.py and task.py files, which contain the key verification scheme implemented using elliptical cryptography. It is known that by connecting to 1955.133.87.171 on port 5555, you can connect to some server:
nc 195.133.87.171 5555password: secch4l*Since the source code is given, it is worth starting with their analysis. You can even run them.
Since I did not have the libnum module, I had to write it myself. It is sufficient to implement the previously mentioned modular inversion function and the Euclidean algorithm it uses:
def egcd(a, b): # Extended Greatest Common Divisor if a == 0: return (b, 0, 1) else: g, y, x = egcd (b % a, a) return (g, x - (b // a) * y, y) def invmod(a, m): # Modular inversion g, x, y = egcd (a % m, m) if g != 1: raise Exception("modular inverse does not exist") else: return x % m So, the
main function from task.py : def main(): print "Auth:“ auth = raw_input() if hashlib.sha1(auth).hexdigest() != "375d5c01ca1b8c3863024d10aac7713472eb5033": # secch4l* print "nope“ return prefix = os.urandom(8) print "Proof of work, please“ print "Prefix is (hexed) ", prefix.encode("hex") test = raw_input().decode("hex") if not test.startswith(prefix) or len(test) > 16: print "nope“ return h = hashlib.sha1(test).hexdigest() if not h.startswith("000000"): print "nope“ return goflag() A string is read, SHA-1 from which must be equal to the specified value (“secch4l *”).
Then a random 8-byte prefix is sent to the client. Bytes are encoded as a hex string. In response, the client must send a string no longer than 16 bytes, so that it begins with the specified prefix, and the first 3 bytes of the SHA-1 value from this string must be zero. If all stages are completed successfully, the goflag () function is called.
The following code fragment connects to the server, sends the password, receives the prefix, calculates and sends the response:
def readLn(sock): a = [] while True: c = sock.recv(1) if '\n' == c: return "".join(a) a.append(c) HOST = "195.133.87.171" PORT = 5555 sock = socket.socket(socket.AF_INET, socket.SOCK_STREAM) sock.connect((HOST, PORT)) print readLn(sock) # Auth: sock.send("secch4l*\n") print readLn(sock) # Proof of work, please s = readLn(sock) print s # Prefix is (hexed) 0b3997e62b9ffbf4 prefix = s.split()[-1].decode("hex") for i in xrange(0x7FFFFFFF): s = "%s%X" % (prefix, i) if hashlib.sha1(s).digest()[:3] == '\0\0\0': break sock.send(s + '\n') After executing this code on the client side, the server performs the goflag () function, which displays something like the following:
EC PASSWORD CHECK
R = 572115218124168948525078362547166172445820217705568707355669424304224832114
SHARED SECRET = R ^ PASSWORD
ENCRYPTED MESSAGE: 7a93846a011e0d0382e94f32d705239e6298169dcec20da5d6
What happens in the
goflag function from task.py : def goflag(): print "EC PASSWORD CHECK" r = random.randint(31337, 1 << 250) R = p256.power(G, r) print "R =", R print "SHARED SECRET = R ^ PASSWORD" S = p256.power(R, PASSWORD) key = p256.derive(S) cipher = encrypt(FLAG, key) print "ENCRYPTED MESSAGE:", cipher.encode("hex") Asymmetric cryptography on elliptic curves is used. The P-256 curve recommended by NIST is selected. The implementation of operations on the curve points does not contain obvious vulnerabilities.
We know the value of R, but without knowing the value of PASSWORD (which is read by the server from the file password.txt) we cannot calculate S. Knowing S would allow us to easily calculate the key. So can encryption be implemented with an error?
The
encrypt function from task.py : def encrypt(msg, key): iv = os.urandom(8) stream = hashlib.sha256(iv + key).digest() stream = hashlib.sha256(stream + iv + key).digest() cipher = iv + xor(msg, stream) return cipher The code shows that the encrypted message is preceded by a random 8-byte initialization vector iv, and encryption is performed as the XOR flag with a gamma generated as the output of two SHA-256 calculations. Without knowing the value of key, getting a gamma is not possible. But how does the key get in the program?
Derive function from task.py:
def derive(self, p): return hashlib.sha256(str((p[0] << 10) / p[1])).digest() It turns out that the value of the point S (consisting of two coordinates - x and y) is used as input SHA-256. In fact, the value of str (int (x * 1024 / y)) is fed to the input of the hash. Since x and y have similar values (these are large integers), the result of arithmetic operations should be close to 1024 (although it may exceed it by several times).
Thus, due to the implementation characteristics of the derive function, the key value can take on a very small number of states. You can simply sort through them all, try to decipher the message on each key, and if it consists only of typed characters - we have achieved success.
import hashlib, ecc enc = "7a93846a011e0d0382e94f32d705239e6298169dcec20da5d6".decode("hex") iv = enc[:8] def decrypt(key): stream = hashlib.sha256(iv + key).digest() stream = hashlib.sha256(stream + iv + key).digest() return ecc.xor(enc[8:], stream) for i in xrange(0x7FFFFFFF): s = decrypt(hashlib.sha256(str(i)).digest()) for c in bytearray(s): if c < 32 or c >= 128: break else: print s # ecc_is_too_s3cure break Thus, the flag is the line "ecc_is_too_s3cure".
Reverse engineering. Shadelt900
Reverse engineering is another popular job category. In addition to CTF, there is a Best Reverser contest in the PHDays competition program.
The task Shadelt900, as well as the previous three, was part of the PHDays IV CTF Quals program, which took place in January 2014. Commands had to decrypt an image called 'derrorim_enc.bmp'. The means used to encrypt it was known - it is called Shadelt9000.exe, but the decryptor could not be found. Here is this image:

A closer look at the Shadelt9000.exe file makes it clear that the application uses OpenGL. Also there is a copyright inflate 1.2.8 Copyright 1995-2013 Mark Adler, indicating that the program uses the popular compression library zlib.
If you can see in the disassembler where the calls to the zlib functions come from, you can quickly find such a piece of code:

At addresses 0x47F660 and 0x47F7B8 are located data arrays, packed zlib. Unpack them:
from zlib import decompress as unZ base = 0x47C000 - 0x7AE00 # data section base ab=open("ShadeIt9000.exe", "rb").read() open("1.txt", "w").write(unZ(ab[0x47F660-base:],-15)) open("2.txt", "w").write(unZ(ab[0x47F7B8-base:],-15)) After unpacking, the 1.txt file contains a pixel shader:
#version 330 uniform sampler2D u_texture; uniform sampler2D u_gamma; varying vec4 texCoord0; varying vec3 v_param; uint func(vec3 co){ return uint(fract(sin(dot(co ,vec3(17.1684, 94.3498, 124.9547))) * 68431.4621) * 255.); } uvec3 rol(uvec3 value, int shift) { return (value << shift) | (value >> (8 - shift)); } const uvec3 m = uvec3(0xff); void main() { uvec3 t = uvec3(texture2D(u_texture, vec2(texCoord0)).rgb * 0xff) & m; uvec3 g = uvec3(texture2D(u_gamma, vec2(texCoord0)).rgb * 0xff) & m; int s = int(mod(func(v_param), 8)); t = rol(t, s); vec3 c = vec3((t ^ g) & m) / 0xff; gl_FragColor = vec4(c, 1.); } File 2.txt contains the vertex shader:
attribute vec3 a_param; varying vec4 texCoord0; varying vec3 v_param; void main(void) { gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex; texCoord0 = gl_MultiTexCoord0; v_param = a_param; } The main information about the pixel shader is highlighted in red:

The variable t is the current element of the processed texture (input file),
and in variable g, the current gamma element (generated in a pseudo-random fashion).
In the variable s, we see some value used later for the cyclic shift s.
The output value is actually calculated as
(rol(t,s) ^ g)And if you run the program several times with the same input file, then for each element the value of g will change from launch to launch, and t and s will remain the same.
Find how gamma is generated:
unsigned char *pbGamma = malloc(cbGamma); srand(time(0)); for (i = 0; i < cbGamma; i++) { pbGamma[i] = rand(); } It can be seen that it depends on the current time.
From the source archive you can find out that the file derrorim_enc.bmp was created on January 21, 2014 at 18:37:52.
We get the value that the time () function would return at that moment:
>>> import time >>> print hex(int(time.mktime((2014,1,21, 18,37,52, 0,0,0)))) 0x52de8640
Now copy the file ShadeIt9000.exe to ShadeIt9000_f.exe and fix it.
At offset 00015557 need bytes
E8 A5 31 01 00replaced by
B8 40 86 DE 52This is equivalent to replacing
call _time on mov eax,52de8640h .Thus, we have received a version of ShadeIt9000_f, which will always encrypt with the same gamma that was at the time of encryption of the file of interest.
Now you need to prepare values that will help decipher the image:
import os bmp=open("derrorim_enc.bmp", "rb").read() hdr = bmp[:0x36] abData = bytearray(bmp[0x36:]) cbBody = len(bmp) - len(hdr) open("00.bmp", "wb").write(hdr + '\0'*cbBody) open("XX.bmp", "wb").write(hdr + '\2'*cbBody) os.system("ShadeIt9000_f.exe 00.bmp") os.system("ShadeIt9000_f.exe XX.bmp") In the file 00_enc.bmp will be the result of encoding the image, consisting of zero bytes. This will be the gamma in its purest form.
The XX_enc.bmp file will contain the result of encoding the image, consisting of bytes with value 2. This will help us know how many bits each byte cyclically shifted.
Finally, decoding Shadelt9000:
def rol(v,i): return (((v<<i) & 0xFF) | ((v>>(8-i)) & 0xFF)) def ror(v,i): return (((v>>i) & 0xFF) | ((v<<(8-i)) & 0xFF)) dRot = {rol(1,i):i for i in xrange(8)} bmp=open("derrorim_enc.bmp", "rb").read() hdr = bmp[:0x36] abData = bytearray(bmp[0x36:]) abGamma = bytearray(open("00_enc.bmp", "rb").read()[0x36:]) abRot = bytearray(open("XX_enc.bmp", "rb").read()[0x36:]) for i,b in enumerate(abGamma): abRot[i] = dRot[abRot[i] ^ b] for i,b in enumerate(abGamma): abData[i] = ror(abData[i] ^ b, abRot[i]) open("derrorim.bmp", "wb").write(hdr + str(abData)) we get:

Above was described the correct, but not the most effective way to solve a task. There is a shorter way.
Immediately behind the vertex shader at addresses 0x47F848 and 0x47F9A0 lies the packed zlib code of the pixel and vertex shader to perform the inverse transform. Perhaps he was accidentally forgotten by the developer of the task. And maybe left intentionally.
The vertex shader codes for encryption and decryption are identical, so there is no point in touching them. And what happens if you replace the pixel shader?
Copy ShadeIt9000_f.exe to ShadeIt9000_d.exe and fix it:
00015775: 60 F6 ==> 48 F8Then run ShadeIt9000_d.exe derrorim_enc.bmp. And we get the decrypted file derrorim_enc_enc.bmp, which (with the exception of small artifacts) is the same as the one we decrypted with the Python script.
That's all for today! Thank you all for your attention, we will be happy to answer questions in the comments.
We remind you that the PHDays IV CTF final will take place on May 21 and 22 during the Positive Hack Days forum. It will be possible to follow the course of the competition not only directly on the court, but also with the help of mobile applications. Follow the news !
See also:
We remind you that registration has already begun for participation in online contests HashRunner and “ Competitive Intelligence ” on PHDays IV!
PS An archive of all PHDays CTF and CTF Quals assignments can be found on the PHDays website . So, if you want to test yourself - go ahead!
PPS A detailed analysis of the tasks presented in the topic was held on a special webinar, which was moderated by Dmitry Sklyarov. Record of the webinar is available at the link: http://my.webinar.ru/record/290241/ .
Source: https://habr.com/ru/post/221991/
All Articles