Private solution of the general problem of electrostatics

From school, we remember the solution of the problem of the distribution of electric charge along an infinite conducting plane in the presence of a point electric charge above the plane. Only a few will remember how the problem of the distribution of electric charge over a conducting sphere is solved analytically, if the point charge is resting somewhere in space. But, I'm sure no one can solve the similar problem of charge distribution in a bottle of Klein. If an external electrostatic field and other conductors are added to such a system, it would be foolish to even think about an analytical solution.

We formulate the general problem of electrostatics as follows:

Given:
- form and location in space of conductors
- charge of conductors
- external electric field (field in the absence of conductors, independent of the position of the conductors)
')
It is necessary to find the charge distribution over the surface of the conductors and the scalar potential of the electric field in the whole space.

The potential as a function of three Cartesian coordinates must satisfy the Poisson equation in the entire space:



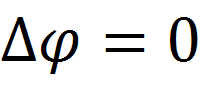
It follows from the uniqueness theorem that if we find a function that satisfies this equation and the boundary conditions, i.e. The solution, this solution will be the only one.

In order to avoid unnecessary complexity, we consider the solution of the problem of the distribution of electric charge over a conducting surface in the presence of an external field , independent of the position and charge of the conducting surface.

We will seek a solution to the problem numerically by the finite element method.

Immediately I warn you that I will not consider theoretically the question of the convergence of my method, but I will confine myself to some facts from practice that support the hypothesis about the convergence of this method, although, perhaps, not to the true solution.

Set the surface parametrically:



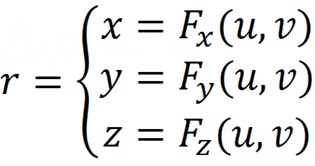
Select the number of u and v - partitions and cover the surface with a network of u and v - lines. At the nodes of the resulting grid, we place the electric charges, the magnitude of which we have to find.
We also choose Nu * Nv points in close proximity to the nodes. We will seek a solution based on the condition that the potential of the electric field at these points is the same. The potential itself will be calculated as a superposition of the potentials created by point charges.

Compose the matrix:

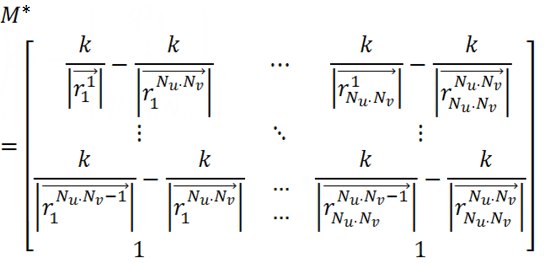
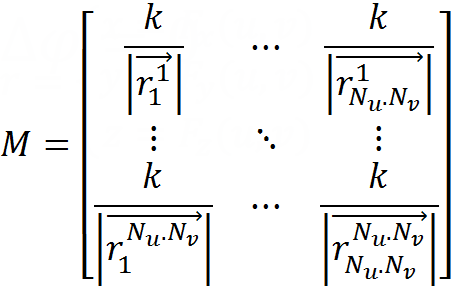- an outline of the matrix of a linear system, which we will solve. The subscripts indicate the position of the charges, the upper - the points of consideration of the potential. These distances are found from the parameterization of the surface.

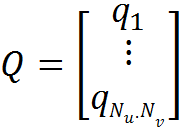- matrix column of unknowns - charge values.

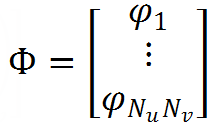- matrix-column potentials of the external field at the points of consideration of the potential.

Then we get the system + MQ = A , where A is a certain constant matrix-column composed of surface potentials unknown to us.

To exclude this potential from the system, we first transfer the matrix F to the right-hand side of the equality, and then subtract the last equation from Nu * Nv-1 of the first equations of the system, which we replace by the normalization condition (the sum of all charges on the surface is equal to the total charge).

Then we get the final linear system with the matrix of the system:



And a column of free members:



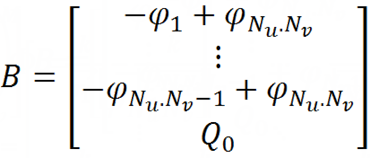
To do away with these pictures with an excessively large font, I’ll give the last expression that defines the result of all the work — a piecewise constant function of the charge surface on the surface (meaning that for u and v belonging to the approximation area with indices of the same name) expressions):



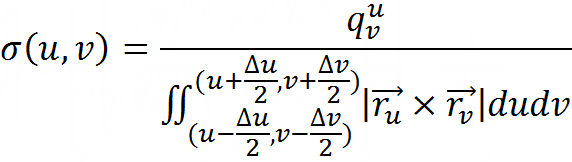
We will solve the system and work with the result in the Mathematica system.

Private solution of the general problem of electrostatics.nb

Let us now look at the work method. We start with a square plate, parametrized in a trivial way. Then the parameters u and v are the Cartesian coordinates of the points of the plate and the area element that stands below the integral is equal to unity.



We got a logical and expected solution.

The solution for the sphere should be a plane, but we get something completely wrong:



I'll explain everything. The point is that the choice of points for placing the charges and considering the potentials depends on the parametrization. And on such a symmetric system as a sphere, we get an asymmetric result due to the fact that the surface charge density is surface in the "Cartesian sense." If we introduced the surface density in a spherical coordinate system, everything would be different.

But it is not all that bad. With an increase in the number of nodes, this figure is compressed (on an automatically constructed graph of math this, however, is not visible) and, I suppose, tends to take the place of the plane.

The surfaces for which a solution is sought must be closed, otherwise a singularity may appear at the edges: as the accuracy increases, the charge density at the edges tends to infinity.

I also decided to solve the problem of charge distribution on a semicircle ("beads") in two ways to test the method.

Method 1. We place the same charges on the beads. No-charge charges. Let’s let them go. In small steps, they will take a stable position. Such a visual method of the Zeidel type with respect to the angular coordinate of the charges:



Method 2. The above-described system corresponds to a half-cylinder in three-dimensional space, for which we solve the problem by our method:



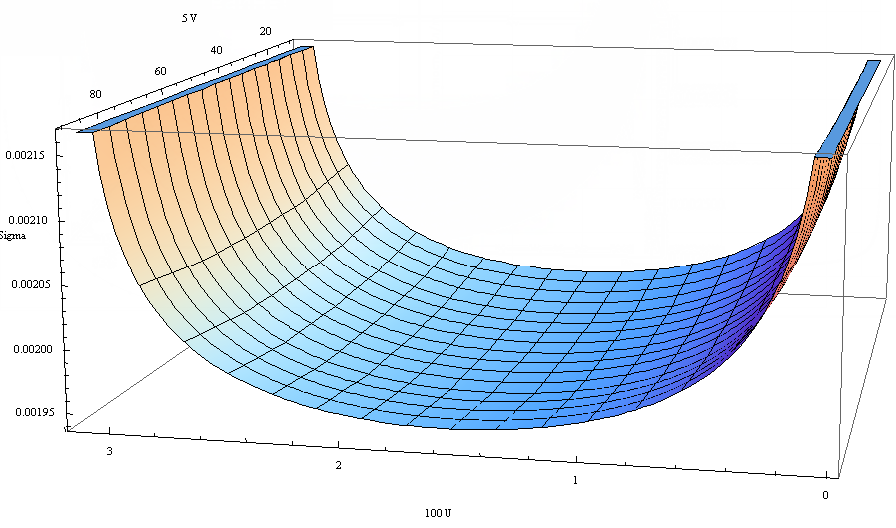
Externally, the solutions are very similar. QED

It is interesting to hear your opinion on the above method for solving the general problem of electrostatics.