Comparison of biological sequences

Tetrapeptide HABR is incomparable

Comparison of sequences of characters is a seemingly simple matter, but, applied to biology, it encounters a lot of problems almost out of the blue. Some problems of modern biology cannot be solved at all at the present stage of development of computer technology. In this article, I will show you on fingers what is so special about biological sequences and why they need special algorithms. Biologists and especially bioinformatics are not recommended to read - there is a risk of dying of boredom.

Biological sequences are the primary structure of biological macromolecules. Namely proteins and DNA / RNA. (There are still carbohydrates, for example, starch, but they consist of identical monomers and therefore uninteresting.) The DNA sequence determines the protein sequence, the protein sequence determines its spatial structure, the structure determines the protein functions, and the set of functions of different proteins is called life. It is the differences in the functioning of different proteins that we, in essence, differ from each other. It is necessary to compare molecules, roughly speaking, for two reasons:
')
1) comparing in pairs the proteins of different organisms, we can say which organisms are more similar to each other, and which are less;
2) comparing simultaneously a dozen or two proteins, we can find structurally and functionally important areas (they are usually identical in related organisms), which is useful when creating artificial proteins (drug design, nanotechnology, in a good sense of the word).


It is better to compare proteins, not DNA, if only because proteins have more “alphabet” (20 amino acids versus 4 nucleotides), and the probability of a coincidence is lower, therefore, we’ll deal with proteins later. Generally speaking, it would be necessary to compare structures, not sequences (since we still do not quite know how the second defines the first); but it so happened that we learned well how to figure out the sequences, and obtaining a spatial structure is a very labor-intensive matter and, in general, many people think art is more likely. Therefore, we have to compare the sequence. Comparison of sequences of biological macromolecules is called alignment - the lines are written one under the other in such a way as to achieve coincidence or similarity of characters in the greatest number of positions. One amino acid residue in a protein corresponds to one letter of the Latin alphabet in the sequence.

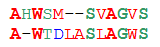
Accounting for the degree of similarity of monomers

We are accustomed to consider two sequences all the more similar, the more characters in them coincide. In biology, this approach is no good. Consider two pairs of sequences:

1 2
ASDLV ASDLV
ATEIV AWDKV

The old Hamming clearly says that the second alignment is better: in the first pair only two of the five characters match, and in the second - three. But let's look at their structures:



S and T, D and E - those residues that distinguish the sequences of the first pair - differ in structure by exactly one carbon atom, L and I - are isomers in general. In most cases, such a difference does not affect the structure of the protein. But replacing a small polar serine with a large non-polar tryptophan or hydrophobic leucine with a charged lysine, as in the second pair, will greatly change the structure of the molecule. Thus, in the first alignment, the sequences are almost identical, and in the second, they are very different.



Accounting for the structural features of the compared characters is quite simple: the so-called ones are used. replacement matrix, as the one in the figure. The greater the number at the intersection of matched letters - the greater the quantitative measure of similarity (called "Score", or "Score").

ASDL V ASDLV
ATEI V AWDKV
Score = 4+1+2+2+4 = 13 Score = 4-3+6-2+4 = 9

Matrices are compiled on the basis of the statistics of amino acid substitutions in proteins with already known structure: the more often there is a substitution of one letter for another, the greater the number at their intersection. The problem is that periodically new matrices appear, better than the previous ones; accordingly, they are all bad and do not take into account something.

Accounting for insertions and deletions

I do not know how others, but I was once struck by how similar the proteins of different organisms are. Where is a person - and where is a rabbit, and serum albumin in both of them differ by only a few amino acids. But they differ by a few: mutational variability is an inherent property of the living. Essentially, assessing the similarity of proteins, we estimate the number of mutations that occurred on the path of the evolutionary transformation of one protein into another. Accounting for mutations of the first type - substitutions - we have discussed above. Two more types - insertions and deletions (deletes) - we will consider now.

Insertions and deletions in bioinformatics are considered as one entity for the simple reason - having two sequences, one of which has an extra letter, we cannot determine which of the sequences is “original”. The hypothetical common ancestor of both organisms died out millions of years ago, so we do not know for sure if there is an insertion or deletion in this case. For this reason, the term "indel" (insertion + deletion) has appeared; In Russian bioinformatics, the term “deletion” or tracing from English “gap” is more common.


Two possible variants of the origin of related sequences. A couple of sequences from the bottom line are real-life “molecules,” at the top, a hypothetical ancestor that could be either on the left or on the right (or not at all).

If there are deletions in alignment, they are penalized. The more deletions - the more points are removed from the account. Again, consider two alignments:

ASGHDLV AMSDCLV
AT--EIV A-TD-VV

In both alignments "dropped out" in two amino acids. In both cases, formally, two mutations occurred. In fact, in the first case, one mutation occurred. Two times long. But one. One evolutionary event. And the probability of it is more than two separate, as in the second example. Therefore, the alignment score on the left should be higher, and the first two sequences should be considered more similar.

To account for deletions is used so-called. an affine penalty consisting of a penalty “for the discovery” and “for the continuation” of the deletion. The first is usually an order of magnitude more than the second (about 10 and 1, respectively, or 10 and 0.1). In the example on the left, we have one discovery and one continuation, on the right, two discoveries.

The problem of accounting for deletions is not limited to this. Depending on the location of the deletion in the molecule, it may, to a greater or lesser extent, affect the structure. Some algorithms, for example, Clustal, take into account "residual-specific fines", some - not. This usually comes down to the fact that deletions in hydrophilic regions — potential loops dangling in the aquatic environment — are fined less than in hydrophobic (potential tightly packed globule nuclei). The question of how these fines should differ, and whether hydropathicity should serve as a criterion for differences, apparently, everyone decides for himself ...


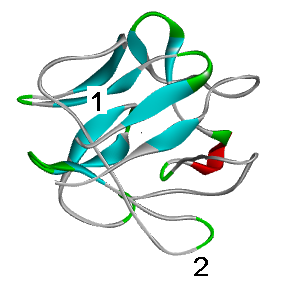
Mutation in the area number 1 - tightly packed and strictly structured (beta strand) globule nucleus - can greatly disrupt the structure of the protein. The mutation in the plot number 2 (unstructured relatively labile loop), most likely, does not affect it.

Alignment Calculation

So far, we have considered the assessment of the finished alignment, without wondering how it turns out. The average protein consists of several hundreds of amino acids, aligning such long lines "by eye" obviously will not work. Although there are different ways of obtaining alignments, the Needleman – Wunsch algorithm and its modifications are now considered optimal. I will omit the essence of the algorithm: the mathematical audience can easily figure it out on its own; the rest should not even try, I cannot explain it in the article on Habré. Suffice it to say that to align two sequences with lengths m and n, an array of the order of size m * n is used; since m and n are numbers of the same order, the order of the array is n ² . Modern consumer computers cope with this calmly. While sequences - two.

In the beginning, I said that by aligning a dozen or two proteins at the same time, we can find structurally and functionally important areas in them. For example, the amino acids in the figure that make up the active center of trypsin-like proteases clearly express themselves in that they are identical in 20 of these proteins (the corresponding positions are indicated by asterisks).


The amino acids that determine the catalytic properties of the enzyme are conservative, i.e. do not change in the process of evolution. The active center of the enzyme must comply with the geometry and chemistry of the substrate up to the atom, so the mutation in it means the “end of career” of the enzyme as a catalyst. In fact, of course, mutations occur anywhere in the molecule; but proteins with a mutation in the functional region make their host unviable, therefore it seems to us that they do not exist.

In conditions when obtaining a complete three-dimensional structure of a protein is still in a certain sense a luxury, the ability to find such patterns is very valuable. The ambush here is that we cannot get a mathematically optimal alignment of even a dozen proteins. If a two-dimensional array is used to align two proteins, then a ten-dimensional, respectively, is needed to align 10 proteins. Even if each sequence has a length of 100 characters (which corresponds to a very small squirrel), the dimension of the array is so huge (100 ¹⁰ ) that a modern computer will count it for thousands of years. About how all the same biologists get out in this situation - I will tell, probably, another time.