Bricks - Universal Puzzle

Consider the ideal homogeneous vertical gravitational field. Suppose we have an unlimited supply of identical perfectly homogeneous bricks of the shape of a rectangular palelepiped. One brick (A) can be put on another (B) so that the center of gravity of brick A is designed within the base of the brick B (that is, the brick A does not fall from the brick B). Now let us take together brick A and B and put them on top of brick B, so that the common center of mass of brick A and B is designed within the base of brick B. While the structure remains stable.


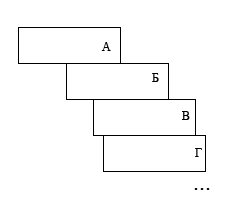
If you continue this process to infinity, what is the maximum horizontal distance that can be achieved between the left edges of the upper and lower bricks so that not a single brick falls?