Breaking Vigenera cipher using frequency cryptanalysis

“Imagine such a situation ... Once, leaving the service at about one in the morning (the manager should set a good example), you notice a crumpled piece of paper sticking out of the door ... The paper is canceled, it smells slightly of musk; the handwriting is clearly feminine and breathes from him a sort of French charm. Now, on second thought, a new employee, Miss Hary, is beginning to seem to you, perhaps, a little too exotic. Her French accent, the invariably black cocktail dress, the black pearl string that accentuates the neckline, and that disturbing musk smell that fills the room when she enters ... She says that she used to work at the Mac Donald Regional Computing Center in Kyokak. Something is wrong here. Wait ... Is Miss Hari spying in favor of the famous French company And Beem Em? And this note - encryption, in which all the secrets of your newest miracle compiler? To catch Miss Hari, the note must be deciphered. But how?"

On Habré already a couple of times flashed articles about the book of Charles Wetherell "Studies for programmers." Before you is a fragment of one of the most interesting, in my opinion, etudes - “The Secrets of the Firm”, the main task of which is to break the Vigenere cipher . Not so long ago, I implemented this sketch, and in my article I will talk about how I did it and what happened in the end.

Task

The author invites us to write a program that will allow to crack the Vigenere cipher, or rather, one of its modifications. The text is encrypted as follows. Compiled table, so-called. Vigenere square: the alphabet is written on top and on the left, then a first permutation of the original alphabet is placed in the first line, the second permutation is cyclically shifted by one position, and so on. As a result, we get a table that associates a character with each pair of characters.
')


Then select a keyword and repeatedly recorded under the source text. Finally, each pair (source symbol; the keyword symbol below it) is encrypted using the table of the corresponding symbol for the pair. For example, the phrase "star of the race" will be encrypted using the key "baggage" and the above table as follows:

Solution idea

Consider the inverse Visioner square, that is, a table that matches a pair (ciphertext symbol; keyword symbol) source symbol.



Let us agree to call the distance between two characters the difference of their positions in the alphabet: for example, the distance between 'a' and 'in' is 2. Then you will notice that if the distance between the i-th and j-th characters of the keyword is d, then the distance between the corresponding characters of the source text is -d. Therefore, if we manage to find a keyword, then we will be able to reduce the Vigener cipher to the simple replacement cipher: each letter of the source text will be replaced with another one, while the correspondence of the letters will be one-to-one. Hacking such a cipher is not difficult.

It remains to find the keyword. Let us know that the length of a keyword is L characters. Then the text can be divided into L groups, each of which will be encrypted using a single character of the keyword, i.e. it will be a simple replacement cipher. In this case, the used permutations of the alphabet will differ only by a shift equal to the sign of the distance between the corresponding symbols of the keyword. Using the methods of frequency cryptanalysis, we will be able to determine these shifts.

Thus, the program will consist of three parts:
1) Determining the length of the keyword
2) Keyword search
3) Search for permutation of the alphabet and text decoding

Keyword length

The length of a keyword is easiest to find using the index index method . This method was proposed by William Friedman in 1922 to crack the original Vigenere cipher, but it will work in our case. The method is based on the fact that the probability of coincidence of two random letters in some rather long text (coincidence index) is a constant value. Thus, if the text is divided into L groups of characters, each of which is encrypted with a simple substitution cipher (remember, this means that L is the length of the keyword), then the coincidence indices for each of the groups will be quite close to the theoretical value of this value; for all other partitions, the coincidence indices will be much lower. The index of matches can be calculated by the formula


(fi is the number of i's of the alphabet in the text, and n is its length)

Below, for example, there are indexes of coincidence for text encrypted with the key “project” (6 characters).



Thus, to determine the length of a keyword, it is necessary to count the coincidence indices for splitting the text into L = 1, 2, ... groups, and then choose from the obtained values ​​the first one, much better than most of the rest. But ... there is a little trick. What if the text is encrypted using a key that can be divided into several similar parts? Below is a table of coincidence indices for the same text as in the first example, but encrypted with the space key (the same 6 characters). How to determine the key length in this case?



I played with various ways and found out that the easiest way is to choose the necessary index like this: you need to take the first index, for which it is fair: 1.06 * EC> EC, i = 1, 2, ... Multiplication by 1.06 is in most cases enough for the real IP exceed the “multiple” IP (in our example, these are indices for L = 12 and 18), but not enough for false indices (for L = 3, 9, and 15) to exceed the real ones.

Of course, my method does not give 100% result. Moreover, if the text is encrypted using a word consisting of identical parts (for example, “tartar”), then the length of the key word will be incorrectly determined anyway (if, of course, we want to find a meaningful keyword): there is no difference between encryption key "tartar" and "tar". Therefore, it is important to give the user the ability to change the key length during the course of the program: for example, it did not fit 6, which means it is worth trying 3 or 12.
Fortunately, for an encrypted note from a book, everything is determined quite simply. Looking at the table of coincidence indices, it is safe to say that the length of a keyword is 7 characters.

Keyword

Now that the key length is found, you can start searching for the keyword itself. First, we need to determine the probabilities of different shifts between the groups into which we split the cipher (recall that each group is encrypted using a certain permutation of the alphabet, and the permutations differ only in the shift of each letter by several positions in the alphabet). To find the probabilities of shifts, I used the idea proposed by the translators of Etudes. If you omit all the mathematical calculations, it is as follows. For each group, we count the number of characters x (x = 'a', 'b', ..., 'I') in it and based on the information about the frequency of letters in Russian, we estimate the probability that the x symbol of the cipher corresponds to the character y (y = 'a', 'b', ..., 'i') of the source code. Comparing the obtained probability tables for different groups, we can calculate the probabilities of shifts r (r = 1, 2, ..., 32) between these groups. As a result, we get a table showing the probability of a shift of r between groups i and j for any two groups and any shift.

Find the keyword itself in two ways. The first way is to find the best shift configuration using (only) the resulting table. A complete search would take a lot of time, so I went the other way. I searched for the key as follows. Take any word of a suitable length and calculate its characteristic — the sum of the probabilities of shifts between every two characters in it (shifts between the characters of the keyword and between the letters of the permutations in different cipher groups coincide with the accuracy of the sign). Now make a small change to the word under study. If, after a change, the characteristic of the word has become better, then we memorize the new word, otherwise we forget the new word and return to the old one. By making random changes in this way, we will quickly find the best word.

The only problem is that the best word is not always the key. Tests have shown that for texts of 1024 characters, the key and the best word often differ by one character. For example, the best word for a note from the book is “Fediska.” I do not know such a word! For shorter texts, the key is completely wrong. Therefore, the search for a key based on only the table had to be abandoned.

The second way to find the key is simple and uninteresting, but effective. We take the dictionary and calculate the characteristics of each suitable word (to increase the speed of the program, I divided the words according to their lengths). The best word we take as the key. This method works correctly even for short (400-500 characters) texts, but it has an obvious disadvantage: if the keyword is not in the dictionary, then the program will not work correctly under any circumstances.

However, if the key is in the dictionary, the second method is much more efficient than the first. Therefore, in my program I used it. This method immediately gave the correct (as it turned out later) keyword - "radish."

Alphabet permutation

Having a keyword, we can modify the text so that it will be encrypted with a simple replacement cipher. To do this, you need to cycle the characters of the L-th group (L = 2, 3, ..., key length) cyclically to the distance between the first and L-th letters of the keyword left alphabetically. After making these changes, it remains for us to find which letters of the source text correspond to the symbols of the ciphertext.
Let's try to do it in the same way we searched for a keyword without a dictionary. Take any table of correspondences between the characters of the source and encrypted texts (for example, suppose that the letter 'a' corresponds to the letter 'a', the letter 'b' - 'b', etc.) and decrypt the text with its help. Calculate the number of various digrams (combinations of 2 letters) in the resulting text. Comparing the result with the reference table, we calculate the characteristic of the received text (I calculated the characteristic as follows:


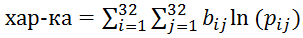
(b_ij is the number of bigrams in the "decoded" text, and p_ij is the probability of meeting a specific digram in the Russian language)

Then we will make random changes to the correspondence table and at each step calculate a new characteristic. If the new feature is better (more) old, remember the changes, otherwise we roll them back. As a result, we get the correct letter correspondence table, and we can restore the original text!

How fast does this permutation search algorithm work? Below is a plot of the permutation characteristics versus the number of iterations for an encrypted note from the book (for other texts, the graphics are similar). The number of iterations is plotted on the horizontal axis, and the characteristic of the received text is on the vertical axis. Characteristic changes occur jerky with each finding the best table, so for clarity, the graph is an interpolated point at which changes occurred. When the line of the graph becomes straight and horizontal, the correct permutation table is found.



It is also interesting to look at the graphs of the dependence of the iteration number on the number of the successful change of the permutation table (on the left) and the characteristics of the text on the change number on the table (on the right).

We see that the text characteristic changes more or less linearly with each change of the permutation table, and the number of attempts required to find a new successful table change grows quite quickly. The dependence of text characteristics on the number of iterations is similar to the logarithmic one. Indeed, the lower plots show that if x is the number of iterations, y is the characteristic and t is the number of the successful change of the table, then x∼e ^ t, y∼t, therefore, y∼ln (x). The logarithm grows rather slowly, but its growth is not limited to asymptotes, so finding a regular correspondence table takes a rather large, but not an infinite amount of work. However, tests show that 10 - 12 thousand iterations are always enough.

Conclusion

After the implementation of the described algorithms and the addition of a graphical interface, we got this program:





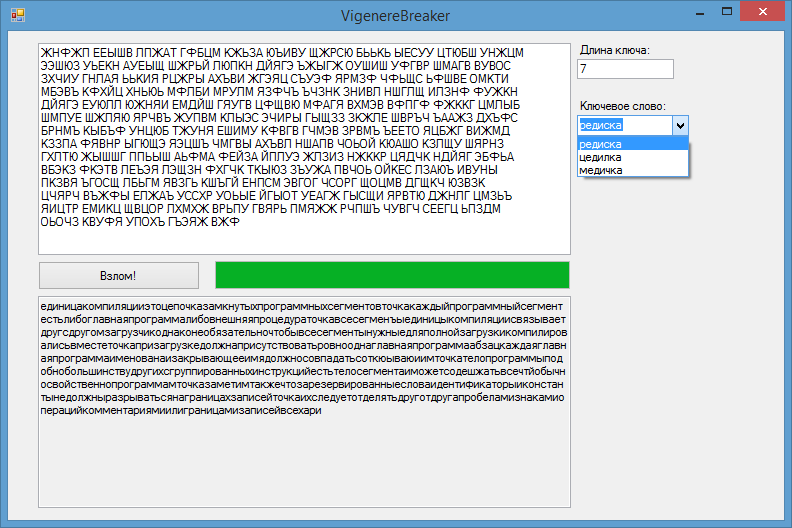
The program successfully decrypts texts of length 400-500 characters and more, the operating time does not exceed 10 seconds. I think this is a good result.

UPD Here is the link to my program. I did it in Visual Studio 2012 and used Windows Forms, so make sure that you have the appropriate redistributable package and the .net Framework 4 installed. You can encrypt text in the program (enter text at the top of the form and the keyword for this; if the keyword will not be entered, it will be selected randomly) or crack the cipher (to do this, enter the ciphertext and click "Breaking!"; if the length of the keyword or the keyword itself is indicated, this data will be used for decryption, otherwise the program pick them themselves).