Classification using the ant algorithm
On Habré, an ant algorithm has already been considered, which allows using simple rules to solve the problem of finding the optimal route. This article describes the application of this algorithm to the classification problem.
For the first time the application of the ant colony algorithm for classification was presented by R. Parpinelli in 2002. The method of extracting classification rules based on the ant algorithm is called AntMiner.
The purpose of the method is to obtain simple rules of the form if the condition is a consequence .
It is assumed that all attributes are categorical. Those. terms are represented as Attribute = Value, for example Gender = Male. AntMiner consistently generates an ordered list of rules. The calculation begins with an empty set of rules and after the formation of the first, all test data units covered by this rule are removed from the test set.
The algorithm is used in the work of a directed graph, where each attribute is associated with as many vertices as it has possible values in the test set. Accordingly, it is assumed that before starting the operation of the algorithm, the sets of attributes and their possible values, as well as the set of possible classes are selected from the test set.

The pseudocode of the algorithm is as follows:
Consider the sequential steps of the algorithm.
')
All edges of the graph are initialized by the initial pheromone value according to the following formula:
, where a is the total number of attributes, b i is the number of possible values of the i-th attribute.
Each rule in the AntMiner algorithm contains an antecedent (term set Attribute = Value) and the class it represents. In the original algorithm, the source data contains only categorical attributes. Suppose that the term ij ≈ Ai = V ij , where A i is the i-th attribute, and V ij is the j-th value of A i .
The probability that this term will be added to the current partial rule compiled by an ant is determined by the following formula:

, where ηij is the heuristic value (to be defined later), τ ij is the pheromone value on this edge of the graph, and I is the set of attributes not yet used by the current ant.
In the traditional ant colony algorithm for solving the transport problem, the weight of the ribs is used together with the pheromone value to decide on the choice of the next vertex. In the AntMiner algorithm, the heuristic is the amount of information - a term used in information theory. Quality here is measured using entropy, to prefer some rules over others:
where k is the number of classes, T ij is a subset containing all data units, where the attribute Ai has the value V ij , | T ij | the number of elements in Tij, freq (T w ij ) is the number of data units that have class w, a is the total number of attributes, b i is the number of possible values of the i-th attribute.
The higher the value of Info T ij , the less likely it is that the ant will choose this term.
After each ant has completed the construction of the rule, the pheromones are updated using the following formula:
τ ij (t +1) = τ ij (t) + τ ij (t) .Q ∀ term ij the current rule
where Q is the quality of the rule, which is calculated by the following formula:
Here TruePos is the number of data units that are covered by the rule and whose class matches the class represented by the rule, FaslePos is the number of data units that are covered by the rule, but the class differs from the class represented by the rule, TrueNeg is the number of data units that are not covered by the rule and whose class does not coincide with the class represented by the rule, FalseNeg is the number of data units that are not covered by the rule, but whose class coincides with the class represented by the rule.
It is also required to perform the recalculation of pheromones, imitating its evaporation. This can be done by a simple normalization of the values, taking into account the updated value of the pheromones.
For a more flexible setting of the algorithm execution, the following formula for updating the probabilities of edges belonging to the current rule is used:

where p is the evaporation coefficient (the value is usually set to ~ 0.1), Q is the quality of the rule described above. Edges not covered by the current rule are simply normalized. This method provides a reduction in the value of pheromone at low Q and an increase at high (unlike the original method).
You can also improve the convergence of the algorithm by introducing a number of so-called “elite” ants, who choose a term for which P = max Pij.
In the original algorithm, the term selection is selected according to the following algorithm:
Where q is a random variable [0..1] with a uniform distribution. Those. the probability density of terms is used.
For the introduction of elite ants, the term selection algorithm changes as follows:
Here q 1 and q 2 are random variables [0..1] with a uniform distribution.
Analogue of AntMiner is the famous Naive Bayes algorithm. According to my experiments on their comparison, AntMiner either slightly surpasses Naive Bayes, or is completely inferior to it on various data sets. The AntMiner implementation presented here and the Naive Bayes implementation from the WEKA library were used for comparison . In addition, AntMiner is significantly inferior in computation time. Perhaps there are situations or some preconditions under which AntMiner turns out to be really the best choice.
For the first time the application of the ant colony algorithm for classification was presented by R. Parpinelli in 2002. The method of extracting classification rules based on the ant algorithm is called AntMiner.
The purpose of the method is to obtain simple rules of the form if the condition is a consequence .
It is assumed that all attributes are categorical. Those. terms are represented as Attribute = Value, for example Gender = Male. AntMiner consistently generates an ordered list of rules. The calculation begins with an empty set of rules and after the formation of the first, all test data units covered by this rule are removed from the test set.
The algorithm is used in the work of a directed graph, where each attribute is associated with as many vertices as it has possible values in the test set. Accordingly, it is assumed that before starting the operation of the algorithm, the sets of attributes and their possible values, as well as the set of possible classes are selected from the test set.

The pseudocode of the algorithm is as follows:
testSet = All Test Suite BYE (| testSet |> max_number_of uncovered_cases) i = 0; RUN i = i + 1; the i-th ant consistently builds a classification rule; Update pheromones on the path represented by the rule of the i-th ant; BYE (i <Number_muravyov) Choose the best of all rules; testSet = cases not covered by the best rule; END OF CYCLE
Consider the sequential steps of the algorithm.
')
Initialization of Pheromone Values
All edges of the graph are initialized by the initial pheromone value according to the following formula:
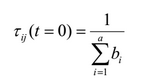
, where a is the total number of attributes, b i is the number of possible values of the i-th attribute.
Rule building
Each rule in the AntMiner algorithm contains an antecedent (term set Attribute = Value) and the class it represents. In the original algorithm, the source data contains only categorical attributes. Suppose that the term ij ≈ Ai = V ij , where A i is the i-th attribute, and V ij is the j-th value of A i .
The probability that this term will be added to the current partial rule compiled by an ant is determined by the following formula:

, where ηij is the heuristic value (to be defined later), τ ij is the pheromone value on this edge of the graph, and I is the set of attributes not yet used by the current ant.
Heuristic
In the traditional ant colony algorithm for solving the transport problem, the weight of the ribs is used together with the pheromone value to decide on the choice of the next vertex. In the AntMiner algorithm, the heuristic is the amount of information - a term used in information theory. Quality here is measured using entropy, to prefer some rules over others:
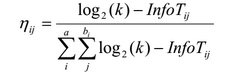
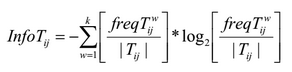
where k is the number of classes, T ij is a subset containing all data units, where the attribute Ai has the value V ij , | T ij | the number of elements in Tij, freq (T w ij ) is the number of data units that have class w, a is the total number of attributes, b i is the number of possible values of the i-th attribute.
The higher the value of Info T ij , the less likely it is that the ant will choose this term.
Update pheromone values
After each ant has completed the construction of the rule, the pheromones are updated using the following formula:
τ ij (t +1) = τ ij (t) + τ ij (t) .Q ∀ term ij the current rule
where Q is the quality of the rule, which is calculated by the following formula:
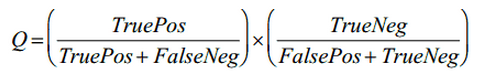
Here TruePos is the number of data units that are covered by the rule and whose class matches the class represented by the rule, FaslePos is the number of data units that are covered by the rule, but the class differs from the class represented by the rule, TrueNeg is the number of data units that are not covered by the rule and whose class does not coincide with the class represented by the rule, FalseNeg is the number of data units that are not covered by the rule, but whose class coincides with the class represented by the rule.
It is also required to perform the recalculation of pheromones, imitating its evaporation. This can be done by a simple normalization of the values, taking into account the updated value of the pheromones.
Improved pheromone update
For a more flexible setting of the algorithm execution, the following formula for updating the probabilities of edges belonging to the current rule is used:

where p is the evaporation coefficient (the value is usually set to ~ 0.1), Q is the quality of the rule described above. Edges not covered by the current rule are simply normalized. This method provides a reduction in the value of pheromone at low Q and an increase at high (unlike the original method).
Elite ants
You can also improve the convergence of the algorithm by introducing a number of so-called “elite” ants, who choose a term for which P = max Pij.
In the original algorithm, the term selection is selected according to the following algorithm:
FOR ALL (i, j) ∈ Ji IF q ≤ ∑ Pij TO Select termij
Where q is a random variable [0..1] with a uniform distribution. Those. the probability density of terms is used.
For the introduction of elite ants, the term selection algorithm changes as follows:
IF q1 ≤ ϕ TO FOR ALL (i, j) ∈ Ji IF q2 ≤ ∑ Pij TO Select termij ANYWAY Choose a term with P = max Pij
Here q 1 and q 2 are random variables [0..1] with a uniform distribution.
Some observations
Analogue of AntMiner is the famous Naive Bayes algorithm. According to my experiments on their comparison, AntMiner either slightly surpasses Naive Bayes, or is completely inferior to it on various data sets. The AntMiner implementation presented here and the Naive Bayes implementation from the WEKA library were used for comparison . In addition, AntMiner is significantly inferior in computation time. Perhaps there are situations or some preconditions under which AntMiner turns out to be really the best choice.
Source: https://habr.com/ru/post/221237/
All Articles