R + C + CUDA = ...

Sometimes there is a need to speed up the calculations, and preferably at once at times. At the same time, it is necessary to abandon convenient, but slow tools and resort to something lower and faster. R has quite advanced features for working with dynamic libraries written in C / C ++, Fortran or even Java. Out of habit, I prefer C / C ++.

R and C

At once I will make a reservation that I work under Debian Wheezy (under Windows, probably, there are some nuances). When writing a library in C for R, consider the following:

• Functions written in C and called in R must be of type void. This means that if a function returns some results, then they must be returned via the function arguments.
• All arguments are passed by reference (and when working with pointers, you need to remain vigilant!)
• In C code, it is desirable to include Rh and Rmath.h (if mathematical functions R are used)

Let's start with a simple function that calculates the scalar product of two vectors:

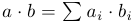
 #include <Rh> void iprod(double *v1, double *v2, int *n, double *s) { double ret = 0; int len = *n; for (int i = 0; i < len; i++) { ret += v1[i] * v2[i]; } *s = ret; } 

Next, you need to get a dynamic library - you can directly through gcc, but you can use this command (by the way, you should remember the output, since it will be useful to us later):

 R CMD SHLIB inner_prod.c 

At the output we get the file inner_prod.so, for which we will use the dyn.load() function. To call the function itself on C, .C() use .C() (there is also .Call() and. .External() , but with slightly different functionality, and hot arguments are sometimes between supporters of .C () and .Call () ). I will only note that when writing C code to call through .C() it turns out to be cleaner and more readable. Special attention should be paid to the correspondence of the types of variables in R and C (in the documentation on the function .C() this is written in detail). Wrapper function on R:

 iprod <- function(a, b) { if (!is.loaded('iprod')) { dyn.load("inner_prod.so") } n <- length(a) v <- 0 return(.C("iprod", as.double(a), as.double(b), as.integer(n), as.double(v))[[4]]) } 

Now you can find out what we have achieved:

 > n <- 1e7; a <- rnorm(n); b <- rnorm(n); > iprod(a, b) [1] 3482.183 

And a small check:

 > sum(a * b) [1] 3482.183 

In any case, he considers it right.

R and CUDA

To take advantage of all the benefits that the Nvidia graphics accelerator provides in Debian, you need to install the Nvidia proprietary driver and the nvidia-cuda-toolkit package. CUDA, of course, deserves a separate huge topic, and since my level in this topic is “beginner”, I will not frighten people with my curves and unfinished code, but allow myself to copy a few lines from the manual.
Suppose you need to raise each element of the vector to the third degree and find the Euclidean norm of the resulting vector:

To make working with GPU somewhat easier, let us use the library of parallel algorithms Thrust , which allows us to abstract from low-level CUDA / C operations. The data are presented in the form of vectors, to which some standard algorithms are applied (elementwise operations, reductions, prefix-sums, sorting).

 #include <thrust/transform_reduce.h> #include <thrust/device_vector.h> #include <cmath> // ,     6   GPU (device) template <typename T> struct power{ __device__ T operator()(const T& x) const{ return std::pow(x, 6); } }; extern "C" void nrm(double *v, int *n, double *vnorm) { // ,    GPU,     *v thrust::device_vector<double> dv(v, v + *n); // Reduce- , ..        power //    . *vnorm = std::sqrt( thrust::transform_reduce(dv.begin(), dv.end(), power<double>(), 0.0, thrust::plus<double>()) ); } 

Using extern "C" necessary here, otherwise R will not see the function nrm (). To compile the code we will now use nvcc. Remember the output of the command R CMD SHLIB... ? Here we adapt it a bit so that a library using CUDA / Thrust can be called from R without any problems:

 nvcc -g -G -O2 -arch sm_30 -I/usr/share/R/include -Xcompiler "-Wall -fpic" -c thr.cu thr.o nvcc -shared -lm thr.o -o thr.so -L/usr/lib/R/lib -lR 

At the output we get DSO thr.so. The wrapper function is almost the same:

 gpunrm <- function(v) { if (!is.loaded('nrm')) dyn.load("thr.so") n <- length(v) vnorm <- 0 return(.C("nrm", as.double(v), as.integer(n), as.double(vnorm))[[3]]) } 

The graph below clearly shows how the execution time increases depending on the length of the vector. It should be noted that if simple operations such as addition / subtraction predominate in the calculations, there will be practically no difference between the time spent on the CPU and the GPU. Moreover, it is very likely that the GPU will lose due to the overhead of working with memory.


')

Conclusion

In fact, in R, operations for working with matrices and vectors are very well optimized, and the need to use a GPU in everyday life does not occur very often, but sometimes a GPU can significantly reduce the calculation time. In CRAN, there are already ready-made packages (for example, gputools ) adapted for working with the GPU ( here you can read more about this).

Links

1. An Introduction to the .C Interface to R
2. Calling C Functions in R and Matlab
3. Writing CUDA C extensions for R
4. Thrust :: CUDA Toolkit Documentation

PS Corrected the first code snippet on the recommendation of vird .