About seven cylinders

After reading the article about seven contiguous cylinders , I wondered: is this really such a difficult task? Or was she just not seriously engaged before?
The position of the infinite cylinder of a known radius in space is given by four independent quantities (it has 4 degrees of freedom). For seven cylinders in general position, 28 values ​​are required. Each condition “two cylinders touch” gives one restriction, only 7 degrees of freedom remain. Six of them - moving space, the latter remains on the configuration itself. That is, we should have one or several one-parameter families of configurations, unless topology interferes (due to which there can be no solutions at all).
Instead of cylinders, it is more convenient for us to work with straight lines. If the diameters of the two cylinders are the same and equal, say, to one, then they touch (externally) if and only if the distance between their axes is one. Consider this fact, and let's go look for seven red perpendicular straight lines ...

Our first task is to reduce the number of variables that describe the system, if possible. To begin with, we will get rid of the movements of space. We say that the first straight line is the Oz axis. Suppose we have another straight line B, the distance from which to Oz is 1. Let the point on B, which is closest to Oz, have coordinates (x, y, z) . Then, as you can see, the condition 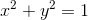, and the directing vector of the straight line B can be specified in the form (-y, x, d) for some d . Thus, the straight line is given by 4 numbers x, y, z, d with one additional condition.
We still have two degrees of freedom of movement of space: a shift along the Oz axis and a turn around it. Fix them by choosing x = 1, y = z = 0 for the second straight line. The remaining 20 unknowns (parameters of the remaining 5 lines) are not limited further.
The condition that the distance between two straight lines with parameters (x ₁ , y ₁ , z ₁ , d ₁ and (x ₂ , y ₂ , z ₂ , d ₂ is 1) can be written as

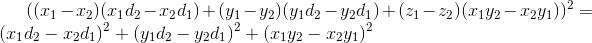
This is the 6th degree equation, connecting 8 unknowns. The degree can be reduced to the fourth, if we take a slightly different parametrization of the line (to say that it passes through the point (x, y, 0) and has a direction vector (u, v, 1) ), but then we lose lines that are perpendicular to Oz.
So, we have a polynomial equation. It remains to compile a system of 20 such equations with 21 unknowns, and think about what to do with it. Remember this, and look for another way.
Let's say that 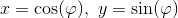for some angle 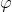. Then the straight line will have three parameters 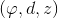for the second line we will have 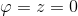, and the equation fixing the distance between two straight lines will look like this: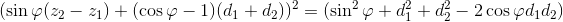

Where 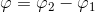. This is a quadratic equation for z ₂ -z ₁ , that is, knowing the magnitudes 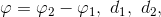we can easily get two possible values ​​of z ₂ -z ₁ .

The action plan will be like this.

1. Let's try a random search. Generate a random set 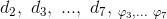. For each straight line from the 3rd to the 7th, we write the condition at a distance of up to the 2nd straight line - it will give us two possible values ​​of the unknowns z ₃ , ... z ₇ . For each of the 32 possible combinations of these values, check how much the distance between the remaining pairs of lines will differ from 1, and choose the best combination. We will try to drive all distances by 1 with some optimization method. If we succeed, we win. If not, repeat a million times.
2. If the search did not return any results, we expand the search. We will go from all possible combinations of z ₃ , ... z ₇ .
3. Note that if we have four contacting cylinders, then the number of cylinders relating to all of them, of course. Let's build the first 4 cylinders in some way (we have 4 degrees of freedom), then we will look (by random search) for as many cylinders that are in contact with them, choose three of them, pairwise distances between the axes of which are as close as possible to 1, and try optimize the resulting set.
4. The same, but first, we look for all touching cylinders, solving a system of 4 polynomial equations (it has 32 roots in a complex field), and then we iterate over all the triples of their axes.
5. If you are unlucky again, we start thinking about what these configurations are and how you can use them.
Unfortunately, nothing came of this plan. Why?

Random Search and Optimization

To optimize a random solution, I used the most tried and tested method - the Newton method. True, for his work, he needs the number of equations to be equal to the number of unknowns, so it was decided to fix the unknown d ₂ (that is, the angle between the first and second straight lines). Find the partial derivatives of z _k -z _m by 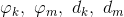- a matter of technology, and we easily build the matrix of the Jacobian of our system of size 10 * 10. True, instead of the usual formula x: = xJ ^-1 f (x), I used the slower movement x: = xc * J ^-1 f (x) , where c changed from 0.1 to 0.001 (because the terrain on which you wander, very uneven and with a lot of local minima). Then it turned out that this method loves to glue straight lines, after which it tries to divide by 0 - I had to explain to him that if 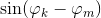for any pair of straight lines is close to zero, then in this attempt we suffered a setback.
Write such a search was easy. After correcting all the unrecorded moments, I launched it - and the first solution was found after a few seconds, at about the 9000th attempt. Over the next 30 minutes, the program found 500 configurations, then on average one of 7500 attempts was successful.
An independent check showed that the solutions were correct - the distances between pairs of straight lines differed from 1 by no more than 10 ^-9 . But, after reviewing the built pictures, I found that many of them are somewhat similar ... So the next question was: which configurations are the same and in what sense?


')


There were no ideas how to approach this issue. Therefore, I remembered the remaining degree of freedom, and decided to see how the cylinders can move without interrupting each other. It turned out that, for example, like this:

Considering the minimum required cylinder length for each configuration (i.e., the maximum distance between the touch points on each cylinder measured along the axis), and plotting graphs, I came to the conclusion that most of the configurations found give the same trajectory. It was easy to build such a trajectory with a small step and count for each configuration a set of invariants. Then for each of the 500 solutions I found, I found the point closest to it on this trajectory. 480 configurations hit right on the path, but the other 20 were new. They behaved like this:

For some reason, this trajectory, although it ends in infinity, but begins in a kind of impasse, to continue through which it fails. I have not solved this riddle yet. In addition, there are signs that two trajectories in some place do not either intersect, or they converge very closely.
In any case, 2-5 points of the plan are not needed.

After going through another 70 million points and finding more than 10,000 solutions, the program did not discover anything new. So only the first minute of the account was spent with benefit ...

UPD: The situation was somewhat worse than I thought. The second family of configurations turned out to be just one of the branches of the first family, but with a different choice of the first two cylinders. And with one end this branch rests not on the point, not on another impassable zigzag - and I have not yet managed to find its continuation.
A random search only gives points from an already found family. It is possible that there are no other configurations (and connected components of the solution set). It will be necessary to check whether the configurations that the Hungarians have found differ in reality.

UPD2: In general, there was an error in the program - some matrix coefficients were wrong (but despite this, the iterations somehow converged :)). After correction, convergence improved markedly, and 100 million start points were processed in about an hour. All the solutions found (about 9 thousand) lay on the main trajectory ... Apparently, there are no more solutions.
By the way, if you solve a system of polynomial equations, then the correct solution is difficult to find. Any polynomial describing the condition that the distance between the lines is 1 will vanish for any pair of parallel lines, so that there will be a lot of parasitic components in the solution set.