Training Round RCC 2014 Warmup

The next season of the largest Russian Olympiad for programmers of the Russian Code Cup started on Saturday, April 19, 2014. Ahead of the new interesting and non-trivial tasks, uncompromising struggle and great prizes.
The jury of the Russian Code Cup prepared one surprise for all participants: on April 17 each of them had the opportunity to evaluate their strengths. At 19:30 Moscow time on the site http://codeforces.ru a training round of the Olympiad took place with a fresh batch of tasks from the creators of the RCC.
')
RCC 2014 Warmup is a test that gave the opportunity to try their hand and understand what to prepare for in the championship rounds. And for “experienced” participants, it turned out to be an ideal opportunity to practice and warm up before the first battles of the RCC 2014.
And if at the Russian Code Cup, tasks for participants are offered only in Russian, then at the Warmup Round tasks were in both Russian and English, which significantly expanded the geography of the meeting. A total of 3265 participants registered for the round.
The conditions of the tasks were very different: it was necessary to help with the selection of participants for the 2214 Russian Code Cup final, restore the testing system data after the fall, hold a football tournament among the participants of the Russian Code Cup, help the cunning boy Gene to get a T-shirt, solve the interesting task of the boy Misha travel on a boat after the final of the Russian Code Cup, organize the final of the Russian Code Cup of 2214 in a large number of hotels, and get a password to access the tasks during their development (the latter has never been able to).
So, let's see how you could best prepare for participation in the championship.
Task 1. Selection
Parsing: First you need to note that if k is greater than or equal to n • m, then the answer is 0. We need to dial n • m - k people. There are three ways to dial them:
• Take rounds of the first type only:
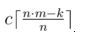
• Take a little rounds of the second type to the number divisible by n:
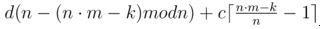
• Take only rounds of the second type: d (n • m - k).
Also in this problem, it was possible to write an over-the-box solution — how many rounds of the first type we take, and how many rounds of the second one.
Task 2. Fail
Parsing: Let's start array a on 105 elements, initially filled with -1, and in the cell with number k we will store the maximum number of the parcel of the k-th participant, which is now there. We will process the parcels sequentially. Let parcel xk be processed. If a [k] <x - 1, then the answer is obviously NO, otherwise the array is updated - a [k] = max (a [k], x).
Task 3. Football
Parsing: Imagine a tournament as a graph. From each vertex there are exactly k outgoing edges. Then just nk edges. In the full graph maximum
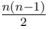 edges, so if n <2k + 1, then the answer is -1. Otherwise, connect the i-th vertex with i + 1, ..., i + k, and loop if necessary.
edges, so if n <2k + 1, then the answer is -1. Otherwise, connect the i-th vertex with i + 1, ..., i + k, and loop if necessary.Task 4. Sly Gena
Parsing: Let's sort the friends by ascending the required number of monitors. We will consider the dynamics on the masks - what is the minimum amount of money you need to pay to solve such and such problems if we took the first i friends. Then the answer should be compared with the answer for i first friends plus the number of monitors that the i-th friend requires. It is not difficult to notice that if you take friends consistently, then you can recalculate the dynamics as a backpack. The running time of this algorithm is O (nlog (n) + n2m).
Task 5. Square table
Parsing: Let's build an array of length n for any n, that the sum of squares of numbers on it is a square:
• If n = 1, then we take [1].
• If n = 2, then we take [3, 4].
• If n is even, then we take
 .
.• If n is odd, then we take
 .
.We are given 2 numbers n and m. Let the array a correspond to the number n, and b correspond to the number m.
Then we construct the final array c in the following way - cij = ai • bj.
Task: 6. Big problems for organizers
Parsing: There are two solutions to this problem.
The first. Suspend for some vertex. Assume for each 3 the most distant vertices in its subtree, as well as the depth for each vertex. Also, prefetch the arrays for the binary upgrade. For each vertex i and power of 2, we assume the following arrays - p [i] [j], up [i] [j] and down [i] [j]. p [i] [j] is the ancestor of the vertex i at a distance of 2j. Up [i] [j] will store the longest path from i to the vertices that are in the subtree of the vertices that are on the path between i and p [i] [j]. down [i] [j] is different from up [i] [j], which stores the path from the vertex p [i] [j].
Now it remains the case for small. We receive a request uv, we are looking for its least common ancestor - w. It remains to find the vertex hu, which will be in the middle of this path. Trim a tree along this vertex, and calculate the longest distance from the vertex u in its tree and the longest distance from the vertex v in its tree. Representing this in the tree, if we do not delete, then we can use our pre-calculated arrays to accurately calculate the value of the longest path.
Solution for O (nlog (n)).
The second. In short. Find the diameter of this tree. Assume there is an answer on the prefix for each vertex. Then, when we answer a query, we find when the path goes into a diameter. On this segment we find the average vertex, and then we respond to the request on the prefix or suffix.
Task: 7. Tricky password
Parsing: The key theoretical idea of this problem is that line 2 coincides with 4, 3 with 5, and so on. Therefore, we need to be able to change something only in the first three lines.
Now the matter remains for the practical part. First of all, let's compress all the values so that they do not exceed 105. We divide the array into segments of length LEN. On each segment we will consider the following - for each value we will store how many times it appears on the cnt prefix, as well as the Fenwick tree, in which the number of numbers on this prefix that occur exactly k times will be stored in cell f [k]. It is easy to see that the first array stores the answer to requests to the second line, and to get an answer for the third line, you need to count f [cnt [k] ... 105]. It is clear the same as doing a recalculation of this dynamics.
Total, we get time to request for
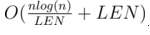 . If we take
. If we take  , the response time to the request will be
, the response time to the request will be 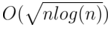 .
.Source: https://habr.com/ru/post/220671/
All Articles