New set to the School of data analysis of Yandex and analysis of the entrance exam
On April 16, a new recruitment to the Yandex Data Analysis School opened, which will last until May 15. In this post I want to tell you about the fate of those who have already completed the SAD, as well as for the first time publicly review all the tasks of our written entrance exam. As always, those who wish will need to fill out a questionnaire and complete the task on the School website , pass a written exam and have an interview.
By the way, if you have acquaintances or their children who are too early to go to the ShAD, but who are promising, tell them about the Computer Science department, which opens this year at the Higher School of Economics with the participation of Yandex. In many ways, it will grow from the School of Data Analysis, but in it we take students and graduates. Therefore, if you are an applicant, then come on April 27 to the presentation of this faculty, where Yaroslav Kuzminov, the rector of HSE, and Arkady Volozh, co-founder of Yandex, will tell all the details about it. We invite everyone.
Since the creation of the SAD, 260 computer science specialists have completed it. We asked two graduates of the School to talk about what they had been taught in it, and to give some advice to those who decided to enroll.
')
Andrei Petrov, a developer at Google’s Munich office.
Alexey Umnov, a graduate of SHAD. Developer in the Yandex morphology group, postgraduate student, VMK MSU.
Debriefing entrance tasks
This time we decided for the first time to publicly parse all the tasks of the written entrance exam for the School of Data Analysis. Only those who have successfully completed the task in the questionnaire are allowed to access it. Last year, out of 617 people, 284 received an invitation to it, and 132 successfully passed and reached the interview.
Sequence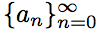 defined recursively.
defined recursively.
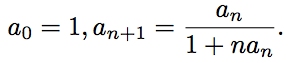
Find the formula for the common term of the sequence.
Decision
We introduce the notation Then
Then 
Besides,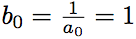 . We get that
. We get that 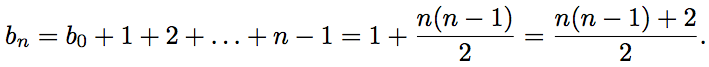
From here we get
We give the set A = {1,2, ..., n}. Among all its subsets, we equiprobably select the k of its subsets A 1 , ..., A k . Find the probability thatA 1 ∩ A 2 ∩ ... ∩ A k = ∅.
Decision
Consider an element i ∈ A. Obviously, the subsets in A containing i and not containing i are equal in number. Thus, the probability that i lies in A j is 1/2. These probabilities are independent for different j . We obtain that the probability that i is contained inA 1 ∩ A 2 ∩… ∩ A k is equal to 1/2 k . Accordingly, the probability that i is not contained in A 1 ∩ A 2 ∩ ... ∩ A k is 1 - 1/2 k . These probabilities are independent in different i . It turns out that the probability that none of the numbers i fell into A 1 ∩ A 2 ∩ ... ∩ A k is equal to (1 - 1/2 k ) n .
Given an array of length n of zeros and ones. Find in it a sub-array of maximum length, in which the number of units is equal to the number of zeros. Limitations: O ( n ) in time and O ( n ) in additional memory.
Decision
Denote the original array by a [・]. Let's get four more arrays of length n : b [・], c [・], d [・] and e []. Let us go in ascending indices and fill the array b [・] according to the rule: b [0] = 2 ・ a [0] - 1, b [ i ] = b [ i - 1] + 2 a [ i ] - 1 as i > 0. In other words, if in the array a [・] zeroes are replaced by -1, then in the array b [・] there will be sums from a [0] to a [ i ]. Fill the arrays c [・] and d [・] minus one. Next, we go in ascending numbers along the array b [・]. If b [ i ] = k , then d [ k ] = i , if in this case c [ k ] = -1, then we assign c [ k ] = i .
Then, when we went through the entire array b [・], fill the array e [・] by the rule e [ i ] = d [ i ] - c [ i ]. Note that if in the array a [・] there is a subarray from a [ m ] to a [ l ], in which there is an equal number of ones and zeros, then b [ m ] = b [ l ] = k . And then c [ k ] is the minimum number i such that b [ i ] = k , and d [ k ] is the maximum. Accordingly, e [ k ] is the maximum distance between m and l , where b [ m ] = b [ l ] = k . Find the maximum of the array e [・]. (Obviously, this can be done in O ( n ) operations.) Let it be equal to e [ j ]. Then the desired subarray is a subarray from a [ c [ j ]] to a [ d [ j ]]
Let be
For which m ∈ [0, 10] I m ≠ 0?
Decision
Repeatedly use the formula:

With this formula we get:
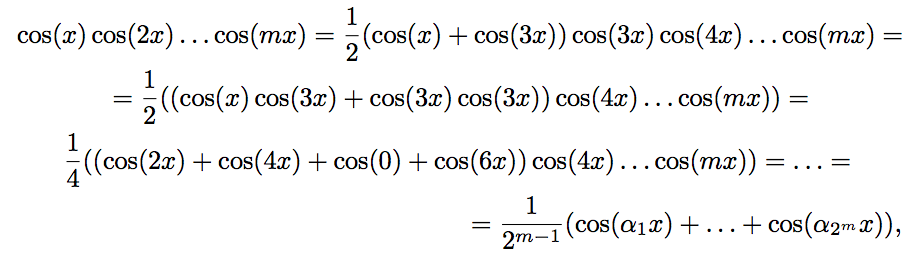 where a i = 1 ± 2 ± 3 ... ± m ∈ Z. It is easy to verify that the parities of all numbers a i will be the same. Moreover, in the cases m = 4k and m = 4k + 3, all a i are even. If a i ≠ 0 , then
where a i = 1 ± 2 ± 3 ... ± m ∈ Z. It is easy to verify that the parities of all numbers a i will be the same. Moreover, in the cases m = 4k and m = 4k + 3, all a i are even. If a i ≠ 0 , then 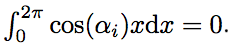
Therefore, for m = 4k + 1 and m = 4k + 2 , I m = 0 . If m = 4k or 4k + 3 , then among a i there is necessarily a zero, since between the numbers 1, 2, ..., m one can so distribute the signs “+” and “-” to get a zero. Really,
(1 - 2 - 3 + 4) + (5 - 6 - 7 + 8) + ... + ((4k - 3) - (4k - 2) - (4k - 1) + 4k = 0,
(1 + 2 - 3) + (4 - 5 - 6 + 7) + ... + (4k - (4k + 1) - (4k + 2) + (4k + 3)) = 0 .
Thus, m = 4k and 4k + 3 , I m = 0 . Answer: when m = 0,3,4,7,8.
Given an undirected graph G without loops. Let us number all its vertices. The adjacency matrix of a graph G with a finite number of vertices n (numbered from 1 to n ) is a square matrix A of size n in which the value of the element a ij equals the number of edges from the i -th vertex of the graph to the j -th vertex.
Prove that matrix A has a negative eigenvalue.
Decision
The statement of the problem is not true. If there are no edges in the graph, then the matrix is zero and all eigenvalues are zero. If there are edges, then A is a symmetric matrix with nonnegative elements and zeros on the diagonal. Let us prove that such a matrix has a non-negative eigenvalue.
It is a known fact that the symmetric matrix is diagonalizable in the real basis. (All eigenvalues are real.) Suppose that all eigenvalues of A are non-negative. Consider the quadratic form q with matrix A in the basis {e 1 , ..., e n } . Then this quadratic form is non-negatively defined, since all eigenvalues are non-negative. I.e On the other hand, let a ij ≠ 0 . Then
On the other hand, let a ij ≠ 0 . Then q (e i - e j ) = a ii - 2a ij + a jj = -2a ij <0. This contradicts the non-negative definiteness of q . So the original assumption is wrong, and A has a negative eigenvalue.
Consider an infinite two-dimensional array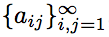 consisting of natural numbers, and each number occurs exactly 8 times. Prove that
consisting of natural numbers, and each number occurs exactly 8 times. Prove that ∃ (m, n): a mn > mn .
Decision
Assume that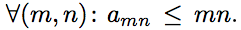 . Choose some k ∈ N and consider a curve on the plane y = k / x . If i, j ∈ N and the point (i, j) lies under the curve y = k / x , then a ij ≤ ij ≤ i ・ k / i = k . Thus, the number of integer points under the curve y = k / x should be no more than 8k . On the other hand, the number of integer points under this curve is not less than
. Choose some k ∈ N and consider a curve on the plane y = k / x . If i, j ∈ N and the point (i, j) lies under the curve y = k / x , then a ij ≤ ij ≤ i ・ k / i = k . Thus, the number of integer points under the curve y = k / x should be no more than 8k . On the other hand, the number of integer points under this curve is not less than 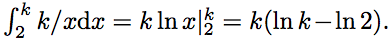 For a sufficiently large k, this number is greater than 8k . Thus, we get a contradiction. Consequently, there is a pair (m, n) such that : a mn > mn .
For a sufficiently large k, this number is greater than 8k . Thus, we get a contradiction. Consequently, there is a pair (m, n) such that : a mn > mn .
Given a matrix of zeros and ones, with the following for each row of the matrix: if there are ones in the row, then they all go in a row (an inseparable group of ones). Prove that the determinant of such a matrix can be equal to ± 1 or 0.
Decision
Rearranging the lines, we can ensure that the positions of the first (left) units do not decrease from top to bottom. In this case, the determinant either does not change, or changes the sign. If the two lines of the position of the first units are the same, then subtract the one in which there are fewer units from the one in which it is greater. The determinant does not change. With such operations, we can ensure that the positions of the first units strictly increase from top to bottom. At the same time, either the matrix will be degenerate or upper triangular with units on the diagonal. That is, the determinant will become either 0 or 1. Since the determinant during our operations either did not change or changed its sign, the initial identifier was ± 1 or 0.
Famous Russian scientists teach in the ShAD. For example, a data analysis course was developed and taught by Ilya Muchnik, a professor at Rutgers University . Once he was the supervisor of Arkady Volozh. The theory of machine learning, without which it is impossible to imagine working with large amounts of data, is taught by Alexey Chervonenkis , a professor at the University of London and one of the founders of the national school of data analysis. The program of the department Computer Science was developed including Ilya Segalovich. We created the SAD to grow a generation of programmers who can apply academic knowledge in applied tasks. Therefore, we teach not only scientists, but also Yandex employees.
Last year we received 617 applications for admission, 284 people were invited to the written exam. But this is not the last test for entering the School. According to the results of the exam, we invite for interviews. Of the 132 people who successfully passed it and reached the interviews, 97 people were enrolled in the first year.
As many of you may remember, ShAD appeared in 2007. Now we have branches in Yekaterinburg, Kiev, Minsk and Novosibirsk. In St. Petersburg, the ShAD branch is open at the Computer Science Center .
Training courses lasts two years. The program is divided into three types of courses: theoretical ("Discrete analysis", "Combinatorics", "Probability", "Theory of complexity"), practical ("Teaching programming in C ++", "Java", "Parallel and distributed computing") and mixed (“Algorithms and data structures”, “Machine learning”, “Computational linguistics”, etc.). You can also study at the correspondence department, communicating with teachers by e-mail and using video lectures.
By the way, if you have acquaintances or their children who are too early to go to the ShAD, but who are promising, tell them about the Computer Science department, which opens this year at the Higher School of Economics with the participation of Yandex. In many ways, it will grow from the School of Data Analysis, but in it we take students and graduates. Therefore, if you are an applicant, then come on April 27 to the presentation of this faculty, where Yaroslav Kuzminov, the rector of HSE, and Arkady Volozh, co-founder of Yandex, will tell all the details about it. We invite everyone.
Stories: one about a googler and one about a Yandex employee
Since the creation of the SAD, 260 computer science specialists have completed it. We asked two graduates of the School to talk about what they had been taught in it, and to give some advice to those who decided to enroll.
')
Andrei Petrov, a developer at Google’s Munich office.
When I was a student, I had the illusion that I already know how to program, and Computer Science is simple. Indeed, after all, I created websites with dynamic content, wrote games, received prizes at competitions and passed exams at the university without any problems. However, it was just a hobby, and I was an amateur. To start the path of a professional, I went to a Yandex school.
There I soon found out that development is not writing code, but observing style, using practices, supporting documentation and testing software. There, for the first time, I was able to closely get acquainted with the highly relevant science of machine learning, and how to learn about its rigorous mathematical foundations, and conduct a lot of experiments on real data, competing with colleagues for quality percentages. There, I broadened my horizons and familiarized myself with the industries that caused only regret from the fact that it is impossible to deal with them all at once: it is pattern recognition, computational linguistics, Internet search, modern algorithms on graphs. In the end, there I met wonderful people, many of whom later became my colleagues and friends.
If you are considering whether to act and remain in the same illusions as I am, now you know what to do. Even if there are no illusions, it is still extremely useful and interesting. And in the science of data analysis, and in the IT-industry professionals are needed. To join their number, you will have to go a long way, and admission to the ShAD is a serious step forward in this direction.
Alexey Umnov, a graduate of SHAD. Developer in the Yandex morphology group, postgraduate student, VMK MSU.
In the ShAD, I received a lot of useful theoretical and practical knowledge. They were useful to me both in projects inside Yandex, and in other areas. For example, in scientific activities, I very actively use the knowledge gained in a machine learning course, as well as various programming skills. It is also worth noting that all the material given in the SAD is quite modern, which is very important for such a rapidly developing field as Computer Science.
I would advise future students to get ready for a fairly large workload and not quite a familiar form of study: to get a good grade for a course, you need to pass homework throughout the semester, and the final control or exam is not enough for this.
Debriefing entrance tasks
This time we decided for the first time to publicly parse all the tasks of the written entrance exam for the School of Data Analysis. Only those who have successfully completed the task in the questionnaire are allowed to access it. Last year, out of 617 people, 284 received an invitation to it, and 132 successfully passed and reached the interview.
Task 1
Sequence
Find the formula for the common term of the sequence.
Decision
We introduce the notation
Besides,
From here we get
Task 2
We give the set A = {1,2, ..., n}. Among all its subsets, we equiprobably select the k of its subsets A 1 , ..., A k . Find the probability that
Decision
Consider an element i ∈ A. Obviously, the subsets in A containing i and not containing i are equal in number. Thus, the probability that i lies in A j is 1/2. These probabilities are independent for different j . We obtain that the probability that i is contained in
Task 3
Given an array of length n of zeros and ones. Find in it a sub-array of maximum length, in which the number of units is equal to the number of zeros. Limitations: O ( n ) in time and O ( n ) in additional memory.
Decision
Denote the original array by a [・]. Let's get four more arrays of length n : b [・], c [・], d [・] and e []. Let us go in ascending indices and fill the array b [・] according to the rule: b [0] = 2 ・ a [0] - 1, b [ i ] = b [ i - 1] + 2 a [ i ] - 1 as i > 0. In other words, if in the array a [・] zeroes are replaced by -1, then in the array b [・] there will be sums from a [0] to a [ i ]. Fill the arrays c [・] and d [・] minus one. Next, we go in ascending numbers along the array b [・]. If b [ i ] = k , then d [ k ] = i , if in this case c [ k ] = -1, then we assign c [ k ] = i .
Then, when we went through the entire array b [・], fill the array e [・] by the rule e [ i ] = d [ i ] - c [ i ]. Note that if in the array a [・] there is a subarray from a [ m ] to a [ l ], in which there is an equal number of ones and zeros, then b [ m ] = b [ l ] = k . And then c [ k ] is the minimum number i such that b [ i ] = k , and d [ k ] is the maximum. Accordingly, e [ k ] is the maximum distance between m and l , where b [ m ] = b [ l ] = k . Find the maximum of the array e [・]. (Obviously, this can be done in O ( n ) operations.) Let it be equal to e [ j ]. Then the desired subarray is a subarray from a [ c [ j ]] to a [ d [ j ]]
Task 4
Let be

For which m ∈ [0, 10] I m ≠ 0?
Decision
Repeatedly use the formula:
With this formula we get:
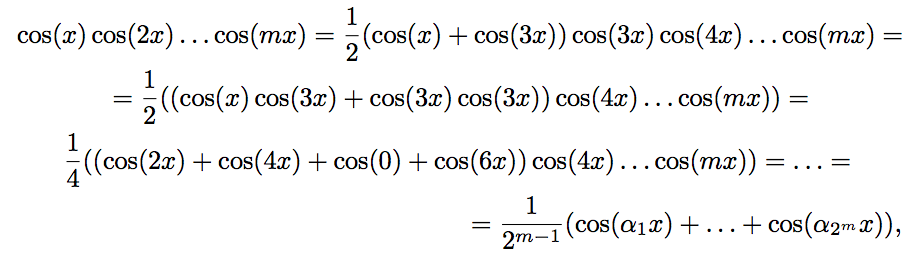 where a i = 1 ± 2 ± 3 ... ± m ∈ Z. It is easy to verify that the parities of all numbers a i will be the same. Moreover, in the cases m = 4k and m = 4k + 3, all a i are even. If a i ≠ 0 , then
where a i = 1 ± 2 ± 3 ... ± m ∈ Z. It is easy to verify that the parities of all numbers a i will be the same. Moreover, in the cases m = 4k and m = 4k + 3, all a i are even. If a i ≠ 0 , then Therefore, for m = 4k + 1 and m = 4k + 2 , I m = 0 . If m = 4k or 4k + 3 , then among a i there is necessarily a zero, since between the numbers 1, 2, ..., m one can so distribute the signs “+” and “-” to get a zero. Really,
(1 + 2 - 3) + (4 - 5 - 6 + 7) + ... + (4k - (4k + 1) - (4k + 2) + (4k + 3)) = 0 .
Thus, m = 4k and 4k + 3 , I m = 0 . Answer: when m = 0,3,4,7,8.
Task 5
Given an undirected graph G without loops. Let us number all its vertices. The adjacency matrix of a graph G with a finite number of vertices n (numbered from 1 to n ) is a square matrix A of size n in which the value of the element a ij equals the number of edges from the i -th vertex of the graph to the j -th vertex.
Prove that matrix A has a negative eigenvalue.
Decision
The statement of the problem is not true. If there are no edges in the graph, then the matrix is zero and all eigenvalues are zero. If there are edges, then A is a symmetric matrix with nonnegative elements and zeros on the diagonal. Let us prove that such a matrix has a non-negative eigenvalue.
It is a known fact that the symmetric matrix is diagonalizable in the real basis. (All eigenvalues are real.) Suppose that all eigenvalues of A are non-negative. Consider the quadratic form q with matrix A in the basis {e 1 , ..., e n } . Then this quadratic form is non-negatively defined, since all eigenvalues are non-negative. I.e
Task 6
Consider an infinite two-dimensional array
Decision
Assume that
Task 7
Given a matrix of zeros and ones, with the following for each row of the matrix: if there are ones in the row, then they all go in a row (an inseparable group of ones). Prove that the determinant of such a matrix can be equal to ± 1 or 0.
Decision
Rearranging the lines, we can ensure that the positions of the first (left) units do not decrease from top to bottom. In this case, the determinant either does not change, or changes the sign. If the two lines of the position of the first units are the same, then subtract the one in which there are fewer units from the one in which it is greater. The determinant does not change. With such operations, we can ensure that the positions of the first units strictly increase from top to bottom. At the same time, either the matrix will be degenerate or upper triangular with units on the diagonal. That is, the determinant will become either 0 or 1. Since the determinant during our operations either did not change or changed its sign, the initial identifier was ± 1 or 0.
A couple more words about school
Famous Russian scientists teach in the ShAD. For example, a data analysis course was developed and taught by Ilya Muchnik, a professor at Rutgers University . Once he was the supervisor of Arkady Volozh. The theory of machine learning, without which it is impossible to imagine working with large amounts of data, is taught by Alexey Chervonenkis , a professor at the University of London and one of the founders of the national school of data analysis. The program of the department Computer Science was developed including Ilya Segalovich. We created the SAD to grow a generation of programmers who can apply academic knowledge in applied tasks. Therefore, we teach not only scientists, but also Yandex employees.
Last year we received 617 applications for admission, 284 people were invited to the written exam. But this is not the last test for entering the School. According to the results of the exam, we invite for interviews. Of the 132 people who successfully passed it and reached the interviews, 97 people were enrolled in the first year.
As many of you may remember, ShAD appeared in 2007. Now we have branches in Yekaterinburg, Kiev, Minsk and Novosibirsk. In St. Petersburg, the ShAD branch is open at the Computer Science Center .
Training courses lasts two years. The program is divided into three types of courses: theoretical ("Discrete analysis", "Combinatorics", "Probability", "Theory of complexity"), practical ("Teaching programming in C ++", "Java", "Parallel and distributed computing") and mixed (“Algorithms and data structures”, “Machine learning”, “Computational linguistics”, etc.). You can also study at the correspondence department, communicating with teachers by e-mail and using video lectures.
Source: https://habr.com/ru/post/220561/
All Articles