Challenge from Richard Feynman
In the wonderful book “You are, of course, joking, Mr. Feynman!” There is an episode that led me to a little practical work, which served as the basis for the creation of this article. It all started from this point:
In the above fragment, the translator was wrong. Paul Olam asks Feynman to calculate the tangent of 10 to the hundredth power. And we are talking about radians, not degrees. It is in this formulation that the task becomes unaffordable for the future Nobel laureate.
I decided to consider a simpler task. Namely, how to find out how much tg (10 °) will be in the hundredth degree? Reflection on this issue was the impetus for a small computational experiment, the results of which I want to share. And I began by asking Google to calculate the named value. The answer was given instantly - 4.2842727e-76.
The tangent is the sine divided by the cosine. Therefore, I began my research by solving a simpler problem. Namely, how to find the sine of 10 degrees and raise it to the hundredth degree. And we need to implement two different methods to ensure the correctness of the result. All calculations were performed on the 1C: Enterprise platform 8.2. A feature of this platform is that the results of calculations are stored in text form, which removes the question of the number of decimal places and, as a result, the accuracy of calculations, at least for addition and multiplication. Now we will decide on the calculation options. The easiest is to calculate the sine and then multiply it by yourself. Since the degree to which we are building an even, then we recall the formula for the cosine of a double angle and we write down:
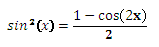
Since during the calculations, we need to control the accuracy of the data used, we will look for the cosine of 20 degrees as the root of the following equation:
4 * cos³ (20 °) -3 * cos (20 °) = 0.5
This equation is derived from the formula for the cosine of the triple angle. To solve the equation numerically, we use the Newton method. In the future, the found value of sin² (10 °) is multiplied by itself 49 times (you can, of course, reduce the number of multiplications, in this case it does not matter).
We give a table with the dependence of the calculations on the accuracy of determining cos (20 °).

From the obtained results it can be seen that an accuracy of 10% is achieved when the input data contains 4 significant digits after the decimal point.
The next item of our research program is the search for an alternative way of calculating the desired work. I did the calculation of the even degree of sine, but the approach used can be applied to the tangent, it just increases the volume of the material presented. Replace the original function with its decomposition into a Fourier series. The decomposition is obtained using the following identity:
cos (α) * cos (β) = 0.5 * (cos (α-β) + cos (α + β))
Here is how we apply it.
sin² (x) * sin² (x) = (0.5-0.5cos (2x)) (0.5-0.5cos (2x))
Open the brackets on the right side and then replace the cosine products with their sum. Then again, the resulting amount is multiplied by (0.5-0.5 cos (2x)) again, open the brackets and once again perform the operation of replacing the product by the amount. Of course, I carried out the procedure outlined using a program in the embedded language of the 1C: Enterprise platform. As a result of these measures, a decomposition of the original function over the basis of cos (2ix) functions was obtained, where i varies from 0 to 25. We then calculate the found decomposition at the point 10 ° = π / 18. We present a table with the values of the basis functions at a given point.
')

For angles in the range from 180 ° to 340 °, the values of the basis functions will differ from the given values only by a sign due to a shift by pi. Now, when there are values of the basis functions and there are expansion coefficients, an alternative calculation can be made. But in this case, the accuracy of the source data should be comparable to the accuracy of the final result, that is, not less than 10⁻⁷⁷. But this is understandable. When we add some values, to obtain the required accuracy, the terms of the sum must be calculated with an error not less than the expected result. The following table shows the calculation results for the described method for different accuracy of the input data.

The given numbers are consistent with our observation about the relationship between the accuracy of the input data and the final result. At the same time, they confirm the reliability of previous calculations.
Below is an image of the processing form that I applied in my research.
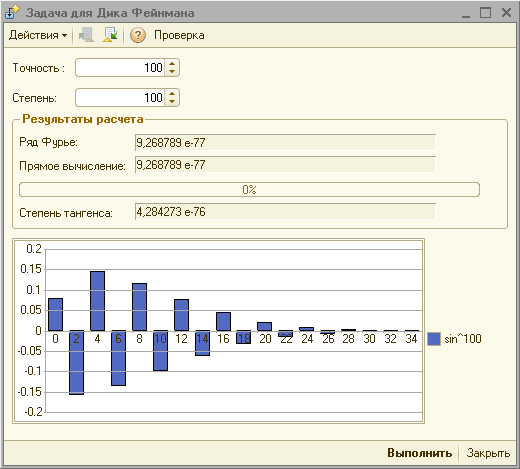
This form, in particular, shows the spectrum of the expansion in a Fourier series of the function sin¹⁰⁰ (x).
And so, with the help of computer technology, which has become much more accessible since the days of the atomic project, we solved the problem. But can it be solved in the mind, or at least get an estimate of the order for the final result. We present a possible sequence of arguments.
Recall that the expansion of the function tg² (x) in powers of sin² (x) is:
tg² (x) = sin² (x) + sin⁴ (x) + sin⁶ (x) + ...
The estimate for sin (10 °) is obtained from the identity:
sin (30 °) = 3sin (10 °) -4sin³ (10 °)
If we drop the cubic term, then the estimate will be 1/6 = 0.166666, since it is underestimated, we take 0.17, and the square of the tangent is estimated at 0.03. Prologize the desired value and get
Ln (tg² (10 °)) = 50 * (- 2 * Ln (10) + Ln (3))
Ln (3) = Ln (e * (1 + 0.3 / e)) ≈1 + Ln (1 + 1/9) = 1.1
Recall that Ln (10) ≈2.30. Then the natural logarithm of the desired quantity will be equal to
50 * (- 4.6 + 1.1) = - 50 * 3.5 = -2.3 * 50 * 35/23 = 2.3 * 50 * (1 + 12/23) ≈-2.3 * 50 * (1 + 0.5 * (1 + 1/24)) = - 2.3 * 50 * 1.52 = -2.3 * 76.
We raise e to the degree obtained and arrive at a result of 10⁻⁷⁶.
In this paper, I could not find an answer to the question that Paul Olam posed. Nevertheless, the above analysis, from my point of view, is a good demonstration of how you can use mathematical tools to solve problems when you need to get to the number. It seems to me that the material presented can be used as a basis for practical training in computational mathematics in high school.
”Paul passes through the dining room, where everyone just stands on their ears. “Hey Paul! They shout. - Feynman - just super! We give him a task that can be formulated in ten seconds, and he gives an answer within one minute with an accuracy of 10 percent. Give him some task! ”Almost without stopping, he says:“ Tangent is 10 degrees to the hundredth degree ”. I'm in trouble: for this you need to divide by up to one hundred decimal places by the number of pi! It was hopeless! ”
In the above fragment, the translator was wrong. Paul Olam asks Feynman to calculate the tangent of 10 to the hundredth power. And we are talking about radians, not degrees. It is in this formulation that the task becomes unaffordable for the future Nobel laureate.
I decided to consider a simpler task. Namely, how to find out how much tg (10 °) will be in the hundredth degree? Reflection on this issue was the impetus for a small computational experiment, the results of which I want to share. And I began by asking Google to calculate the named value. The answer was given instantly - 4.2842727e-76.
The tangent is the sine divided by the cosine. Therefore, I began my research by solving a simpler problem. Namely, how to find the sine of 10 degrees and raise it to the hundredth degree. And we need to implement two different methods to ensure the correctness of the result. All calculations were performed on the 1C: Enterprise platform 8.2. A feature of this platform is that the results of calculations are stored in text form, which removes the question of the number of decimal places and, as a result, the accuracy of calculations, at least for addition and multiplication. Now we will decide on the calculation options. The easiest is to calculate the sine and then multiply it by yourself. Since the degree to which we are building an even, then we recall the formula for the cosine of a double angle and we write down:
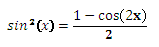
Since during the calculations, we need to control the accuracy of the data used, we will look for the cosine of 20 degrees as the root of the following equation:
4 * cos³ (20 °) -3 * cos (20 °) = 0.5
This equation is derived from the formula for the cosine of the triple angle. To solve the equation numerically, we use the Newton method. In the future, the found value of sin² (10 °) is multiplied by itself 49 times (you can, of course, reduce the number of multiplications, in this case it does not matter).
We give a table with the dependence of the calculations on the accuracy of determining cos (20 °).

From the obtained results it can be seen that an accuracy of 10% is achieved when the input data contains 4 significant digits after the decimal point.
The next item of our research program is the search for an alternative way of calculating the desired work. I did the calculation of the even degree of sine, but the approach used can be applied to the tangent, it just increases the volume of the material presented. Replace the original function with its decomposition into a Fourier series. The decomposition is obtained using the following identity:
cos (α) * cos (β) = 0.5 * (cos (α-β) + cos (α + β))
Here is how we apply it.
sin² (x) * sin² (x) = (0.5-0.5cos (2x)) (0.5-0.5cos (2x))
Open the brackets on the right side and then replace the cosine products with their sum. Then again, the resulting amount is multiplied by (0.5-0.5 cos (2x)) again, open the brackets and once again perform the operation of replacing the product by the amount. Of course, I carried out the procedure outlined using a program in the embedded language of the 1C: Enterprise platform. As a result of these measures, a decomposition of the original function over the basis of cos (2ix) functions was obtained, where i varies from 0 to 25. We then calculate the found decomposition at the point 10 ° = π / 18. We present a table with the values of the basis functions at a given point.
')

For angles in the range from 180 ° to 340 °, the values of the basis functions will differ from the given values only by a sign due to a shift by pi. Now, when there are values of the basis functions and there are expansion coefficients, an alternative calculation can be made. But in this case, the accuracy of the source data should be comparable to the accuracy of the final result, that is, not less than 10⁻⁷⁷. But this is understandable. When we add some values, to obtain the required accuracy, the terms of the sum must be calculated with an error not less than the expected result. The following table shows the calculation results for the described method for different accuracy of the input data.

The given numbers are consistent with our observation about the relationship between the accuracy of the input data and the final result. At the same time, they confirm the reliability of previous calculations.
Below is an image of the processing form that I applied in my research.

This form, in particular, shows the spectrum of the expansion in a Fourier series of the function sin¹⁰⁰ (x).
And so, with the help of computer technology, which has become much more accessible since the days of the atomic project, we solved the problem. But can it be solved in the mind, or at least get an estimate of the order for the final result. We present a possible sequence of arguments.
Recall that the expansion of the function tg² (x) in powers of sin² (x) is:
tg² (x) = sin² (x) + sin⁴ (x) + sin⁶ (x) + ...
The estimate for sin (10 °) is obtained from the identity:
sin (30 °) = 3sin (10 °) -4sin³ (10 °)
If we drop the cubic term, then the estimate will be 1/6 = 0.166666, since it is underestimated, we take 0.17, and the square of the tangent is estimated at 0.03. Prologize the desired value and get
Ln (tg² (10 °)) = 50 * (- 2 * Ln (10) + Ln (3))
Ln (3) = Ln (e * (1 + 0.3 / e)) ≈1 + Ln (1 + 1/9) = 1.1
Recall that Ln (10) ≈2.30. Then the natural logarithm of the desired quantity will be equal to
50 * (- 4.6 + 1.1) = - 50 * 3.5 = -2.3 * 50 * 35/23 = 2.3 * 50 * (1 + 12/23) ≈-2.3 * 50 * (1 + 0.5 * (1 + 1/24)) = - 2.3 * 50 * 1.52 = -2.3 * 76.
We raise e to the degree obtained and arrive at a result of 10⁻⁷⁶.
Conclusion
In this paper, I could not find an answer to the question that Paul Olam posed. Nevertheless, the above analysis, from my point of view, is a good demonstration of how you can use mathematical tools to solve problems when you need to get to the number. It seems to me that the material presented can be used as a basis for practical training in computational mathematics in high school.
Source: https://habr.com/ru/post/220075/
All Articles