Encoding of binary data into a string with an arbitrary length alphabet (BaseN)

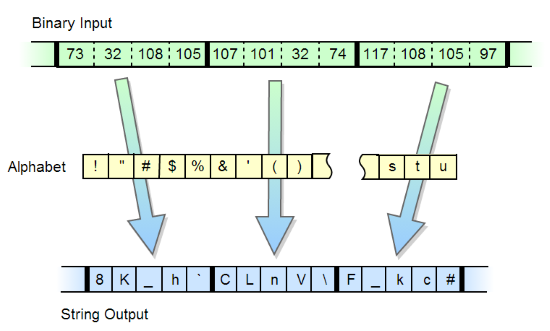Everyone knows the algorithm for converting an array of bytes to a string base64. There are a large number of varieties of this algorithm with different alphabets, with and without tail symbols. There are modifications of the algorithm in which the length of the alphabet is equal to other powers of two, for example 32, 16. However, there are more interesting modifications in which the length of the alphabet is not a multiple of the power of two, such are the algorithms base85 , base91 . However, I did not come across an algorithm in which the alphabet could be arbitrary, including a longer length than the 256. The task seemed interesting to me, and I decided to implement it.

Immediately posting a link to the source code and demo on js . Although the developed algorithm is rather theoretical, I found it necessary to describe the details of its implementation. Practically, it can be used, for example, for cases when a shorter string length is more relevant than its size in bytes (for example, in quineas).

Arbitrary alphabet

To understand how to synthesize such an algorithm, I decided to look into a particular case, namely the base85 algorithm. The idea of ​​this algorithm is as follows: the input data stream is divided into blocks of 4 bytes, then each of them is treated as a 32-bit number with a high byte at the beginning. By successively dividing each block by 85, 5 digits of the 85-base number system are obtained. Then each digit is encoded by a printed symbol from the alphabet, 85 characters in size, and output to the output stream, with preservation of order, from the most significant digit to the least significant one.

But why was the size chosen 4 bytes, i.e. 32 bits? But because this achieves optimal compression, i.e. the minimum number of bits is enabled (2 ^ 32 = 4294967296) with the maximum number of characters (85 ^ 5 = 4437053125). However, this technique can be extended for any other alphabet. Thus, a mathematical system was compiled to find the number of bits at which compression will be maximized:
')
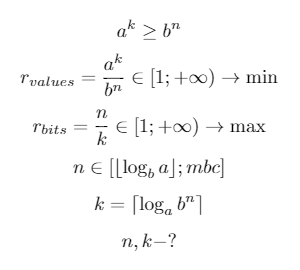a is the size of the alphabet A.
k - the number of encoded characters.
b - the base of the number system.
n is the number of bits in the number system b for representing the k characters of the alphabet A.
r - compression ratio (the more - the better).
mbc is the maximum block size in bits.

⌊X⌋ is the largest integer less than x (floor).
⌈X⌉ is the smallest integer greater than x (ceiling).

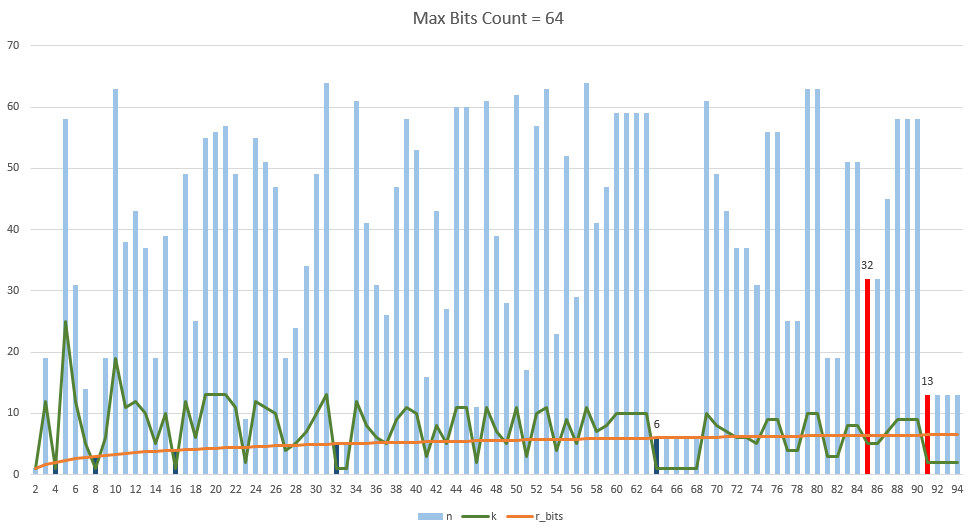
Then, using this technique, optimal combinations of bits and the symbols encoded in them were found, which were shown in the figure below. The maximum block size is 64 bits (this number was chosen due to the fact that with a larger number it is necessary to use large numbers). As you can see, the compression ratio does not always increase with an increase in the number of characters (this can be seen in the region between 60 and 91). The red bars represent known encodings (85 and 91). Actually, from the diagram we can conclude that such a number of characters for these encodings was not chosen for nothing, since it uses the minimum number of bits with a good compression ratio. It should be noted that when increasing the maximum block size, the diagram may change (for example, for base85 encoding with 64 bits, the block size will be 32 bits, and the number of characters - 5 with 1.25 redundancy. If the maximum block size is increased to 256 bits, then block size will be equal to 141 bits with 22 characters and redundancy 1.2482).

Coding stages

So, step by step, the encoding process is as follows:

1. The calculation of the optimal block size (number of bits n ) and the number of corresponding characters ( k ).
2. The representation of the source string as a sequence of bytes (UTF8 is used).
3. The division of the original byte sequence into groups of n bits.
4. Convert each group of bits to a number with a base system of a .
5. Calculating the tail bits.

The implementation of the first stage was discussed above. For the second stage, the method was used to represent the string as an array of bytes (in C # it is embedded Encoding.UTF8.GetBytes () , and for JS it was written manually by strToUtf8Bytes and bytesToUtf8Str ). Further, the next three stages will be discussed in more detail. The inverse transformation of a sequence of characters into an array of bytes looks the same way.

Bit block coding

private void EncodeBlock(byte[] src, char[] dst, int ind) { int charInd = ind * BlockCharsCount; int bitInd = ind * BlockBitsCount; BigInteger bits = GetBitsN(src, bitInd, BlockBitsCount); BitsToChars(dst, charInd, (int)BlockCharsCount, bits); } private void DecodeBlock(string src, byte[] dst, int ind) { int charInd = ind * BlockCharsCount; int bitInd = ind * BlockBitsCount; BigInteger bits = CharsToBits(src, charInd, (int)BlockCharsCount); AddBitsN(dst, bits, bitInd, BlockBitsCount); } 

GetBitsN returns the number of the length of the BlockBitsCount bit and starting at bit numbered bitInd .
AddBitsN appends a number of bits of the length of a BlockBitsCount bit to an array of dst bytes in the bitInd position.

Converting a block of bits to a number system with an arbitrary base and back

Alphabet is an arbitrary alphabet. For the inverse transform, use the pre-calculated Inverse Alphabet InvAlphabet . It is worth noting that, for example, for base64 the direct order of bits is used, and for base85 - the reverse ( ReverseOrder ), _powN - powers of the length of the alphabet.

 private void BitsToChars(char[] chars, int ind, int count, BigInteger block) { for (int i = 0; i < count; i++) { chars[ind + (!ReverseOrder ? i : count - 1 - i)] = Alphabet[(int)(block % CharsCount)]; block /= CharsCount; } } private BigInteger CharsToBits(string data, int ind, int count) { BigInteger result = 0; for (int i = 0; i < count; i++) result += InvAlphabet[data[ind + (!ReverseOrder ? i : count - 1 - i)]] * _powN[BlockCharsCount - 1 - i]; return result; } 

Tail bit processing

The most time was spent on solving this problem. However, in the end, it turned out to create a code for calculating the main and tail bits and symbols without using real numbers, which made it possible to easily parallelize the algorithm.

• mainBitsLength - the main number of bits.
• tailBitsLength - tail number of bits.
• mainCharsCount - the main number of characters.
• tailCharsCount - the tail number of characters.
• globalBitsLength - the total number of bits (mainBitsLength + tailBitsLength).
• globalCharsCount - the total number of characters (mainCharsCount + tailCharsCount).

Calculation of the main and tail number of bits and characters when encoding.

 int mainBitsLength = (data.Length * 8 / BlockBitsCount) * BlockBitsCount; int tailBitsLength = data.Length * 8 - mainBitsLength; int globalBitsLength = mainBitsLength + tailBitsLength; int mainCharsCount = mainBitsLength * BlockCharsCount / BlockBitsCount; int tailCharsCount = (tailBitsLength * BlockCharsCount + BlockBitsCount - 1) / BlockBitsCount; int globalCharsCount = mainCharsCount + tailCharsCount; int iterationCount = mainCharsCount / BlockCharsCount; 

Calculation of the main and tail number of bits and characters when decoding.

 int globalBitsLength = ((data.Length - 1) * BlockBitsCount / BlockCharsCount + 8) / 8 * 8; int mainBitsLength = globalBitsLength / BlockBitsCount * BlockBitsCount; int tailBitsLength = globalBitsLength - mainBitsLength; int mainCharsCount = mainBitsLength * BlockCharsCount / BlockBitsCount; int tailCharsCount = (tailBitsLength * BlockCharsCount + BlockBitsCount - 1) / BlockBitsCount; BigInteger tailBits = CharsToBits(data, mainCharsCount, tailCharsCount); if (tailBits >> tailBitsLength != 0) { globalBitsLength += 8; mainBitsLength = globalBitsLength / BlockBitsCount * BlockBitsCount; tailBitsLength = globalBitsLength - mainBitsLength; mainCharsCount = mainBitsLength * BlockCharsCount / BlockBitsCount; tailCharsCount = (tailBitsLength * BlockCharsCount + BlockBitsCount - 1) / BlockBitsCount; } int iterationCount = mainCharsCount / BlockCharsCount; 

Javascript implementation

I decided to create a port of this algorithm and JavaScript. For work with large numbers the jsbn library was used . For the interface used bootstrap. The result can be seen here: kvanttt.imtqy.com/BaseNcoding

Conclusion

This algorithm is written in such a way that it is easy to port into other languages ​​and parallelize (this is in the C # version), including the GPU. By the way, about modifying the base64 algorithm under the GPU using C # is well written here: Base64 Encoding on a GPU .

The correctness of the developed algorithm was tested on the algorithms base32, base64, base85 (the sequences of the resulting characters were the same except for the tails).