Digital Image Stabilization from Stationary Cameras - Correlation Approach

Introduction

I decided to write this article after reading the article “ Massively parallel image stabilization ”, which describes an algorithm for image stabilization from PTZ cameras. The fact is that at one time I had implemented an algorithm for image stabilization from stationary cameras, which is used in the MagicBox IP video server and some other products of Synesis , in which I currently work. The algorithm turned out quite successful in its speed characteristics. In particular, it is very effectively implemented algorithm for finding the offset of the current image relative to the background. This efficiency made it possible to use its main elements (of course, with some modifications) to accompany objects, as well as to check them for immobility.

The stabilization algorithm includes the following main elements: the detection of an offset for the current frame, the compensation of a given offset, and the periodic updating of the background against which stabilization occurs. Below I will paint in detail each of them.

Fig. 1 Image stabilization is sometimes very useful.

Offset detection of the current frame

The basic approach on which the correlation approach is based on the definition of bias can be briefly described as follows:
1) Take the central part of the background image. The amount of indentation is determined by the maximum possible offset that we want to determine. The central part should not be too small, otherwise the correlation function (see below) will not have enough data for stable operation.
2) In the current frame, a part of the same size is selected, but offset from the center of the picture.
3) For each offset, a certain metric is calculated that describes the correlation of the central part of the background and the current image. For this, for example, the sum of squared differences for each point of these two images or, for example, the sum of absolute differences for each point can be used.
4) The offset, for which the correlation is maximal (less than the sum of quadratic differences or the sum of absolute differences), will be the desired offset.

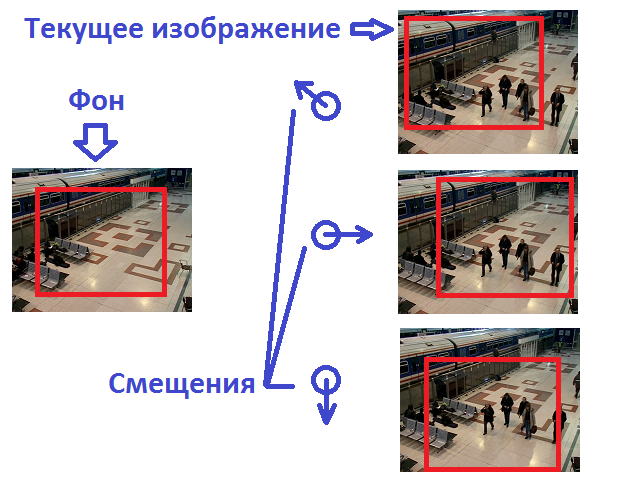
Fig. 2 Offset of the current frame relative to the background.
')
Naturally, if such an approach is applied in the forehead, then the speed of the algorithm will be catastrophically low, even though the speed of the correlation functions may be very high. This is not surprising, since we will need to go through all the options for a possible displacement of images relative to each other (the complexity of the algorithm can be estimated as O (n ^ 2), where n is the number of image points).

The first optimization is the use of not exhaustive search of all possible options, but using the gradient descent method: at the beginning, the correlation is calculated in the 3x3 region for zero offset, then the offset with the maximum correlation is selected and the process is repeated until a local maximum is detected. This method is much faster, but in the worst case of large displacements, it will have O (n ^ 1.5) complexity, which is also not acceptable.

Fig.3 Search for the maximum of the correlation function. Gradient descent.

The way out of this situation is the use of multiscale images (each zoom level reduces the image twice). Now we will look for the local maximum of the correlation for the maximum scale, and then on a smaller scale, we will consistently refine it. Thus, the complexity of the algorithm is reduced to O (n), which is already quite acceptable.

Fig.4 Multiscale image.

Subpixel accuracy

If you compensate for the camera shake with pixel accuracy, then the stabilized image will still twitch quite noticeably. Fortunately, this can be fixed. If you carefully analyze the vicinity of the correlation function near the maximum (see Fig. 3), you can see that the values of the function are not symmetric about the maximum, which means that the maximum is not located at point (3, 2), somewhere between it, and point (1, 4). If we approximate the behavior of the correlation function near the maximum by the paraboloid A * x ^ 2 + B * x * y + C * y ^ 2 + D * x + E * y + F = 0 , then the task of refining the coordinates of the maximum will be reduced to selecting such parameters of the paraboloid, at which its deviation from the actual values at known points is minimal. Experience suggests that the accuracy of the refinement thus obtained will be of the order of 0.1–0.2. When compensating for jitter with such accuracy, the stabilized image is almost no twitching.

Offset compensation

The offset compensation for the whole shift is performed as follows: shift the current image to the found shift with the opposite sign. Empty areas near the edge fill background. For subpixel shift, we perform compensation by bilinear interpolation. In this case, however, a slight blur of the stabilized image is possible. If this is critical, then bicubic interpolation can be applied.

Background update

As a background, you can use just any previous frame. However, the quality of stabilization is noticeably improved if an image averaged over many frames is used as a background. It is advisable to update the background periodically to compensate for possible changes in illumination on the scene. When updating the background, you need to make sure that the background value is quite contrasting and non-uniform. Otherwise, the correlation function will not have a clear maximum, which greatly reduces the accuracy of the stabilizer. It is also highly undesirable to have moving objects in the background.

Work in tandem with motion detector

If the stabilizer is paired with a motion detector, then the background update process for it is greatly simplified. Usually the motion detector already has in its composition a background averaged over many frames, relative to which it determines the presence of motion. The same background can be used for stabilizer operation. The stabilized image from the stabilizer in turn reduces the number of false alarms of the motion detector. You can also use the fact that the movement detector in its work process receives a mask of areas with the presence of movement. This mask obtained by the motion detector in the past frame can be used when calculating the correlation function to exclude areas with motion. Which also has a positive effect on the image stabilizer.

Pros of the proposed approach:

1) High speed algorithm. In particular, for image stabilization with a resolution of 1280x720 in BGRA32 format on a Core i7-4470 processor (1 core is involved), the algorithm requires 1.5 milliseconds.
2) Camera jitter compensation with sub-pixel accuracy.

Disadvantages of the proposed approach

1) Image stabilization in the current implementation is possible only for stationary cameras.
2) Only the spatial shift of the camera is detected and compensated; the camera rotations are not compensated.
3) The background must be sufficiently clear and non-uniform, otherwise the correlation function will have nothing to catch on. Therefore, stabilization will work poorly in the dark or in fog.
4) The background must be fixed. The work of the stabilizer against the background of traveling waves is also impossible.

Notes on practical implementation

To begin with, we note that to determine the shift, it is quite enough to use only a gray image, the color characteristics have almost no effect on accuracy, but naturally slow down the calculations.

When implementing a stabilizer, it is desirable to use optimized functions for working with images. I used the Simd library for this purpose. In particular, you can find:
1) SimdAbsDifferenceSum and SimdAbsDifferenceSumMasked - for calculating the correlation function.
2) SimdReduceGray2x2, SimdReduceGray3x3, SimdReduceGray4x4 and SimdReduceGray5x5 - for building multi-scale images.
3) SimdBgrToGray - for gray image.
4) SimdShiftBilinear - to compensate for the shift.