Bayes

Morpheus’s left hand contains 7 blue and 3 red tablets, and 5 blue and 8 red tablets in his right hand. You close your eyes and take a pill - it turns out to be red, but you don’t know from which hand you took it. What is the probability that you took it from the right hand?

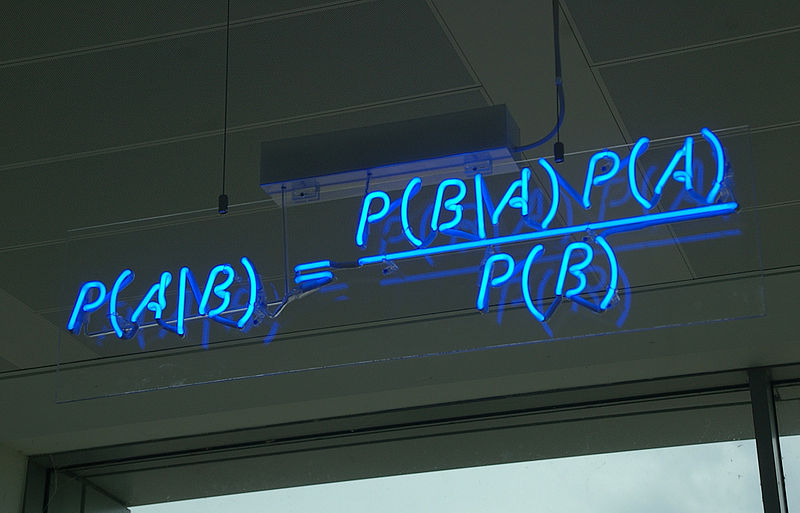
April 17, 1761 - the day of the death of Thomas Bayes.

Under the cut, the results of what is in RuNet, in addition to standard things such as Bayes theorem , Bayesian network , Naive Bayes classifier , Bayesian spam filtering



')

"Humanitarian" articles

Intuitive explanation of the Bayes theorem ( Eliezer Yudkowski )



An Intuitive Explanation of an intuitive explanation of the Bayes theorem, made by Elke Yudkowski (Luke Muehlhauser)



Harry Potter and the methods of rational thinking. Chapter 20. Bayes theorem



What is Bayesianism (Kai Sotala)



The Reverend Bayes Theorem (Bird Kivi, Computerra)



Bayesian ideas for managers (contains helpful links at the end)



For those who want to go to a more complex level - a couple of paradoxes associated with the terrier and the confirmation of hypotheses

Paradoxes

Parado Monty Hall



The Raven Paradox

If a person has seen a lot of red apples, will this increase his confidence that all ravens are black?



Paradox of regularity

00111100000100110100000111010111101000111101011010

11100011100011100011100011100011100011100011100011

What sequence is written by man, and what is the result of throwing a coin?



Birthday paradox

There is a group of 60 people. What is the probability that two people will have the same day and month of birth?



St. Petersburg paradox

The following task is considered. Entering the game, the player pays a certain amount, and then throws up a coin (the probability of each outcome is 50%) until the eagle drops out. When the eagle falls, the game ends, and the player receives a win calculated according to the following rules. If the eagle fell at the first throw, the player gets 2 ^ 0, at the second throw - 2 ^ 1 and so on: at the n-th throw - 2 ^ (n-1). In other words, the gain increases from throw to throw twice, running through powers of two - 1, 2, 4, 8, 16, 32, and so on.



It is necessary to determine what size of the entry fee makes such a game fair.



The Paradox of Sleeping Beauty

(The paradox is a probabilistic problem, which has several different, in its own way correct answers, and demonstrates how statistics can be manipulated. Adam Elga is considered the author of the paradox. In 1999, the problem caused a Usenet flame )

Subject (Sleeping Beauty) is given an injection of sleeping pills. Symmetric coin is thrown. In the case of a falling eagle: it is awakened, and the experiment ends there. In case of a loss of a tails: they wake her up, make a second injection (after which she forgets about waking) and wakes the next day without throwing a coin (in this case, the experiment goes on for two days in a row). This whole procedure is known to Belle, but she has no information on what day she was awakened.



Imagine yourself in the Sleeping Beauty place. You are woken up. What is the probability that the coin fell headlong?



Solution 1.

You do not have any information about the result of a coin fallout and previous wake-ups. Since it is known that the coin is fair, it can be assumed that the probability of tail ½.

Solution 2.

Let's make experiment 1000 times. Sleeping beauty is woken up on average 500 times with an eagle and 1000 times with tails (because in the case of tails, sleeping beauty is asked 2 times). Therefore, the probability of tails 2⁄3.

More paradoxes

Articles on Habré

Recommender systems: Bayes theorem and naive Bayes classifier



Naive Bayes classifier in 25 lines of code



Bayesian analysis in Python



SMS filtering of spam using a naive Bayes classifier (R code)



Cookies from Watson (mention of "Bayes surprise")



Probabilistic models: Bayesian networks



Introduction to Bayesian Methods



Expert system for predicting personal characteristics of a person based on Bayes theorem



Course lectures "Startup". Peter Thiel. Stanford 2012. Session 17



Lectures from Yandex for those who want to spend the holidays with benefit. Discrete analysis and probability theory



PS

Bayesian inference in marketing