Seven of the most interesting tasks of the RCC for all the years according to Andrei Stankevich
On the eve of the first qualifying round of the Russian Code Cup, which will be held on April 19, we decided to tell you about the seven most interesting tasks of the RCC in the entire history of the championship in the opinion of Andrei Stankevich - associate professor of the ITMO computer technology department, laureate of the President's Award in education, laureate ACM-ICPC Founder's Award, IBM Special Award Winner for Coaching Achievement.
We remind you in order to take part in the Russian Code Cup, you need to register on the site http://russiancodecup.ru/ (registration will be open before the start of the third qualifying round).
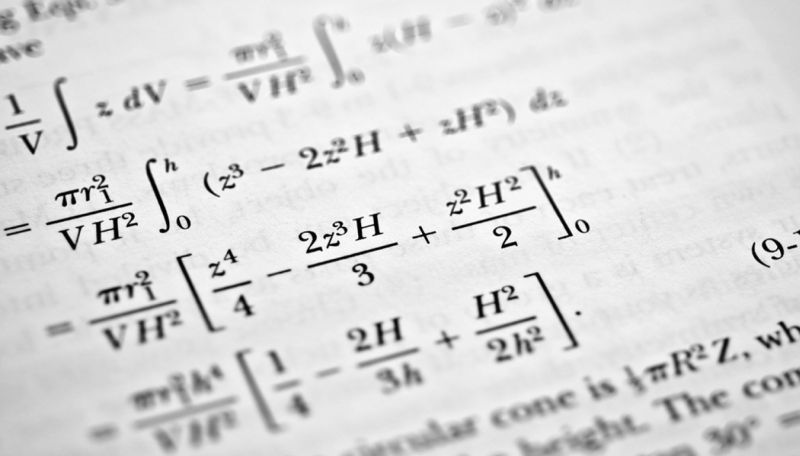
2011, Final Round, “B” Inverse Problem of the Bug
2011, Final Round, “D” Archiver
2012, 2nd qualifying round, “C” Tetrahedron
2012, Qualifying Round, "F" Prince
2012, Final Round, "E" Mixing the deck
2013, Qualifying Round, “E” Lasers
2013 Final Round, “D” Robot
')
1) 2011, Final Round, “B” Inverse Problem of the Bug
Parsing:
In this task, it was required for a given number k to build a maze in which the number of paths from the left upper to the lower right cell would be equal to k, provided that it is allowed to move only to the right and down.
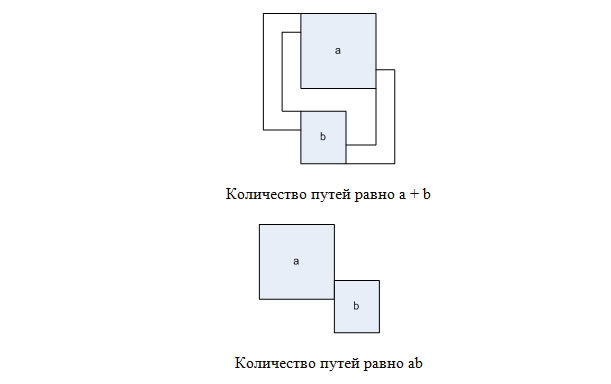
Note the following. Suppose we have two mazes in which the number of ways to get from the top left to the right bottom cell is a and b, respectively.
Then, placing them in parallel, as shown in the figure, we can get a maze for which there are a + b ways to get from the top left to the bottom right cell. And placing them in series - get a maze in which ab paths.
Note that there are two paths in an empty 2 × 2 maze, and one path in a 1 × 1 maze. Therefore, by expanding the number k into a binary number system and using the method described, one can obtain a maze with k paths from the upper left to the right lower cell.
An example of such a maze for k = 19 is shown in the figure.
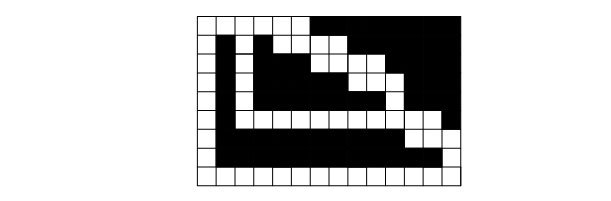
Note that for each digit of the number k, 5 cells are required horizontally, and 2 60 > 10 18 , therefore, the above scheme allows you to create a maze no larger than 300 × 300 in size, which is required in the condition of the problem.
2) 2011, Final Round, “D” Archiver
Parsing:
There are at least two different approaches to this problem: dynamic programming or a greedy algorithm.
Imagine the process of archiving a sequence in the form of a tree: each character of each of the intermediate sequences will be a vertex of the tree, the children of the vertex will be two characters that are “glued together” during the archiving process to the specified one. The original numbers are written in the leaves, and the task is to write down the numbers in all intermediate vertices, while the penalty for archiving is equal to the number of vertices that have different numbers in the children.
The solution using dynamic programming is arranged as follows: at each vertex u we will store the minimum total penalty p [u] [x] for the subtree if we write the number x at this vertex. Note that at the vertex it is sensible to write down only the number that occurs in one of the leaves in the subtree, so the total number of options that should be considered is O (n log n).
Recalculation is carried out as follows: consider the vertex u with children v and w. Suppose we plan to write the value of x. If both p [v] [x] and p [w] [x] are defined, then one of the options to put x in u is to put x in both children, the price of this option is p [v] [x] + p [w ] [x]. There is also an option to put x only in one child. Suppose we plan to put x in v, then the cost of this variant is p [v] [x] + minp [w] + 1, where minp [w] is the minimum value of p [w] [y] over all y.
An alternative solution to using DP is a greedy solution: for each vertex we will store a list of all possible values, putting one of which to the top we will get the minimum penalty in the subtree. It turns out that in order to find the optimal set for a vertex, it suffices to try to put only optimal values in its children. Moreover, if the lists of optimal values for children overlap, then you need to take one of these numbers. If they do not intersect, then any of the meanings of each of the children will do.
The proof of the correctness of the above algorithm is left as an exercise.
3) 2012, 2nd qualifying round, “C” Tetrahedron
Parsing:
Let me remind you that a tetrahedron is a polyhedron whose faces are four triangles (in other words, a triangular pyramid).
It all starts with the fact that we iterate over possible matches of matches to the edges of a tetrahedron. Denote the desired tetrahedron as ABCD. He has six edges: AB, AC, AD, BC, BD and CD. Let's go through all 6! = 720 variants, which match corresponds to which edge. Now it remains to verify that the corresponding tetrahedron exists.
How to check the existence of a tetrahedron? There are at least three solutions.
The first solution is based on the calculation of the volume of the tetrahedron. The simplest solution is to find a formula for calculating the volume of a tetrahedron over faces. This task is not an easy task by itself; here’s the formula:
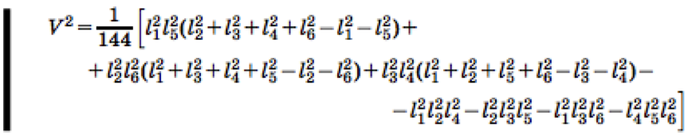
Accordingly, if the right-hand side of the equation turns out to be negative or the triangles in the faces cannot be constructed (triangle inequality), then the tetrahedron will not converge.
For those interested - here this formula is derived .
The second approach to solving the problem is geometric. First, make sure that ABC and BCD exist. Now try to make a tetrahedron. It is clear that when constructing a volumetric figure, a problem can arise only with the last edge - it can be either too long or too short. Therefore, this solution proposes to find the range of the length of the last edge.
There are two limiting ways of placing faces in which the tetrahedron turns into a flat figure. The first is when the faces are rotated 180 degrees relative to each other (CAB and CBD), and the second is when they are “folded” and form a “zero angle” (CA'D and CDB). All admissible positions of faces relative to each other are in the range between these boundary ones. The last edge (AD) reaches its greatest length in the first limiting variant (AD), and the smallest - in the last (A'D). Consequently, a tetrahedron will exist if this length of the last edge fits into the range found by us (from A'D to AD).
In order to find the distance between points A and D and A 'and D, we first find their coordinates, taking one of the common vertices for triangles as zero, and draw the abscissa axis through one of the edges emanating from this vertex. To find the coordinates of all the other vertices in this coordinate system is quite simple: through the aspect ratios and the cosines of the corners, we determine the vertex positions in polar coordinates (angle, distance), after which we translate them into a Cartesian coordinate system. Knowing the coordinates of the vertices, it is quite simple to calculate the maximum and minimum distances between unbound vertices.
The program should check whether the length of the remaining face fits in the specified ranges. If yes, then a tetrahedron of such lengths can be “assembled”.
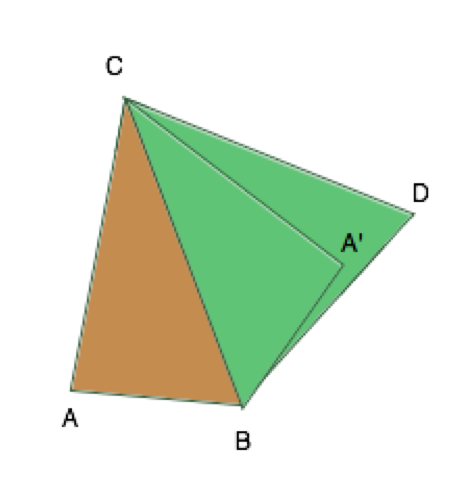
The third way is also geometric. First you need to check the existence of all triangles with the specified sides. If at least one triangle cannot be built on the indicated values of the sides, then a tetrahedron cannot be built either. To verify it is necessary to check the inequality of a non-degenerate triangle: either of its sides must be strictly less than the sum of the two others.
In many cases, this decision was limited; Meanwhile, there are situations when triangles with specified sides can be constructed, and a tetrahedron cannot be assembled from them.
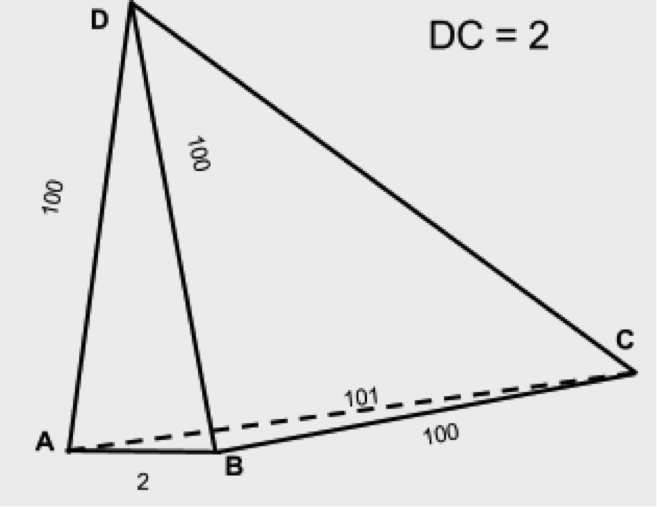
For example, if we have faces (100,100,2,101,100,2), then the triangles (100,100,2) and (101,100,2) formally satisfy the triangle inequality, but the tetrahedron of these triangles cannot be folded. From the figure we see that the edge AC is almost parallel to AB, which means that the distance from D to C will almost not change at any inclination of the face ABD relative to AB, from which we can conclude that DB is almost perpendicular to BC. In this case, the DC can be roughly estimated as the root of the sum of the squares of the legs, that is, the DC should be about 10, not at all 2, as we assumed in the condition.
Therefore, in addition to checking for triangles in the edges, it is necessary to perform an additional check for triangular angles. There are two necessary and sufficient conditions for the existence of a triangular angle:
The plane angle is through the cosine theorem for the triangle.
In total, 1088 solutions were sent for verification, of which only 74 were correct (7%). 8% of participants of the Russian Code Cup QR2 coped with this task. The first decision came from a participant with the nickname AVictor 30 minutes after the start of the round.
4) 2012, Qualifying Round, "F" Prince
Parsing:
In this task, you need to find the minimum time during which the prince will get to the princess along a one-dimensional corridor, without falling into any trap. Known schedule, size and location of the appearance / disappearance of traps, as well as the speed of the prince. Since the corridor is one-dimensional, the prince can move either towards the princess, or from her, or not move anywhere at all. Obviously, there are situations where there is no way out, and the prince will not get to the princess - in this case, you need to withdraw Impossible.
The solution to this problem is to start by depicting traps on a plane, where the x coordinate is the position in the corridor and the y coordinate is the time. Now the problem can be reformulated in terms of this plane: you need to get from point (0, 0) to point (x, y) with minimum y, while it is allowed to move vertically up (stand still), diagonally right up and left up (move along the corridor) and it is forbidden to enter certain rectangles (traps). Being on the border of a rectangle is allowed.
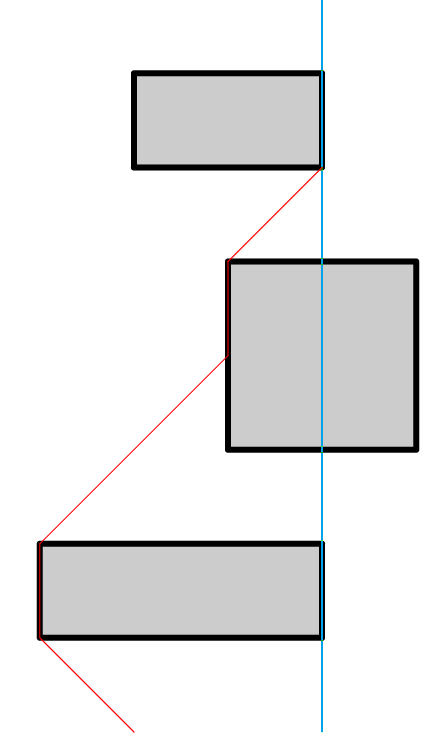
The optimal path in such a task will consist of many parts of the same type, each of which will consist of moving along one of the diagonals to the coordinate corresponding to the border of one of the rectangles, followed by moving vertically up to the upper corner of this rectangle. Thus, the key points are the upper left and upper right corners of each rectangle, and you need to find out about them if you can get there.
When moving diagonally, we will support the set of rectangles above the current position. Since it is possible to be on the border of rectangles, we will not take into account rectangles that start or end at the current “corridor” coordinate. The rectangles will be stored in a set, ordered along the bottom edge. Such a set will be called a cut. For storing sets, you can use data structures like red-black or Cartesian trees or priority queues. The lower edge of the lower rectangle will be called the cut edge. If the slice does not contain rectangles, then we will consider its edge as infinity.
Since at any movement the time coordinate increases, we will consider the angles of the rectangles in the non-decreasing order of this coordinate. Considering the next angle, we will try to move from it diagonally in both directions. Movement is carried out according to the coordinates corresponding to the boundaries of the rectangles. Reaching the next coordinate, we check whether it is possible, moving vertically upwards, to get to the corresponding upper corner of some rectangle. You can reach the angle if this angle is not above the edge of the current slice. It is also necessary to check that the movement did not rest on the edge of one of the rectangles starting at the given coordinate. If you managed to reach the coordinates of the door x, then you need to update the current answer. If, when moving from one coordinate to another, the edge of the slice was exceeded, then at the transition the lower edge of the rectangle was reached, and the movement must be stopped.
Alternately examining all the angles and stepping in both directions from each of them, we find the minimum possible answer or information that the door is not reachable. The described algorithm performs O (n2 log n) operations, since it is necessary to pass from each of the O (n) angles along the O (n) diagonal of different coordinates and check the O (n) rectangles. Also, for each angle, it is necessary to perform O (n log n) operations in order to maintain the cutoff, since O (n) rectangles must be added and removed from the cutoff.
The following are possible options for passing by the rectangles that you need to remember to process.
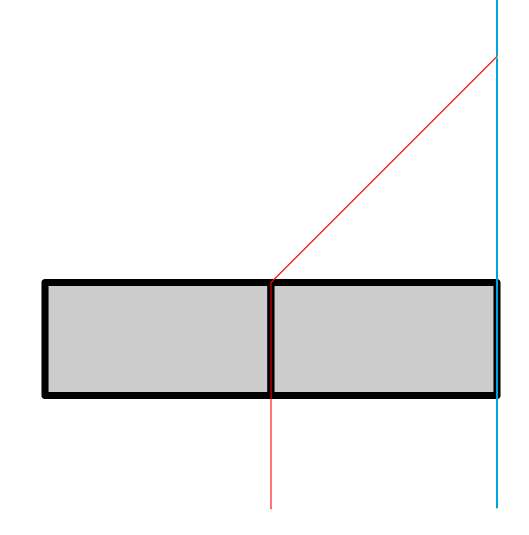
and
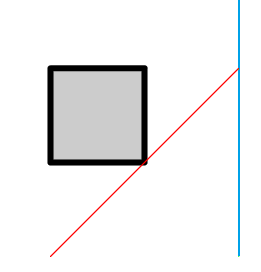
At the same time on the next test it is impossible to have time to get to the door.
This task is also not an easy one - only 23 people decided it, the first was Kulikov Egor at 100: 18. It is worth noting Epifanov Vladislav, who sent the solution to this problem, the last for him, 2 minutes before the end of the tour. Vladislav won first place both in qualifying and in the qualifying round.
5) 2012, Final Round, “E” Mixing the deck
Parsing:
Sergey Melnikov , a student at NRU ITMO, tells about the task of mixing the deck.
In this task, you need to think about the mixing mechanism of the deck, which allows you to mix it ideally (that is, to make no two identical cards follow each other) for the minimum number of card block movements from the middle to the end of the deck. . Initially, the deck is sorted by non-decreasing dignity. Given the number of different advantages of cards, the order of cards in the deck, the number of decks.
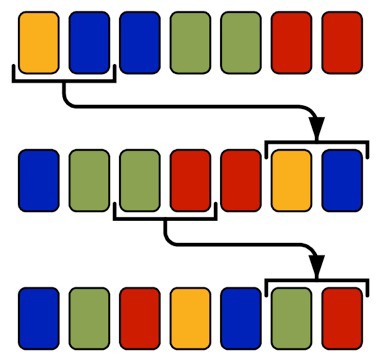
Detailed statement of the problem
Let's call a conflict a situation in which two identical cards stand in a row:
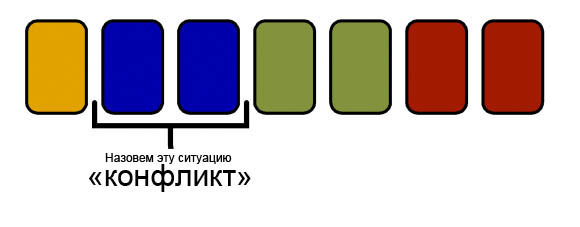
We call the body the original sequence of cards, which we will gradually reduce by transferring the cards to the tail. The tail will be formed in such a way that the cards in it do not form conflicts.
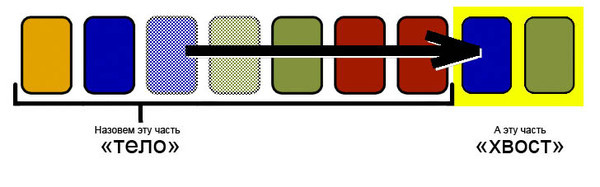
Transform the original sequence into a sequence of conflicts and will work with the new sequence. We will call the color of the conflict the number written on the cards that form it. Each time transferring a piece of cards to the end of the deck, we will choose its ends inside the conflicts.
We denote the number of conflicts by K. Since one move operation removes no more than two conflicts, the task cannot be solved faster than in ⌈K / 2⌉ operations (here and later in the description there are constructions ⌊ ... and ⌈ ... ⌉ - these are rounding down and up respectively ).
Let M be the maximum number of conflicts of the same color and we will call these conflicts themselves “maximal”. We will learn how to solve the problem in the case when M = ⌈K / 2⌉.
Also I remind you that according to the conditions of the task the deck is sorted by non-decreasing value.
For example, in deck 1122333344, the number M will be equal to 3 (three conflicts 33), the total number of conflicts is 6. In this case, M = ⌈K / 2⌉.
In this case (not an example), there are two options:
Solutions for these cases are optimal, since the lower bound of the number of operations ⌈K / 2⌉ is reached. So, we are able to solve the problem optimally, when the number of “maximum” conflicts is half of all conflicts (rounded up). We will call this case the base case.
Now we classify the initial situations by the maximum number of cards of the same denomination in a row. We will call these cards maximum and denote their number as Q.
Now we will delete the last couple of conflicts each time, which can be removed (the last two conflicts of different colors) (C 1 , C 2 ). If in the process we get into the base case, then we will decide how we solve it. If no more conflicts remain, then the problem is solved.
We prove that new conflicts will not arise. Consider the color of the last conflict Z, we will transfer pairs of conflicts (X, Z) until Z ends, while Z remains at the end, and we get the tail Z (X 1 , Z) (X 2 , Z) .... If Z-conflicts end, then there will be a transition to (X, Y) conflicts, that is, a pair (X k , Z) (X k + 1 , Y), with X k + 1 Z.
In the transition to the basic case of conflict does not occur, because after the transfer of the pair (X, Z), neither X nor Z can become maximum (M). Since M ≠ Z, then either Z is over and there is no conflict (X, Z) (Z, ...), or Z is after M, that is, we get a continuation (X, Z) (M, Z).
Since we remove a couple of conflicts at each step, or use the base case, the constructed solution is optimal and works in “K / 2” operations.
You may notice that there is no need to store information about which numbers and in what order are written in the tail, since there are no conflicts there. The sequence of values can be maintained using a Cartesian tree using an implicit key, with the total running time being O (N log N). Also, if at some point we determine that there are no conflicts at the end of the body, then we can reduce the length of the body and, accordingly, increase the tail. It is possible to consider all cases when a segment moves, and make sure that the body will always look like: the prefix of the original array with no more than two subcut segments cut out. Based on this fact, it is possible to implement the solution in O (n), but to solve this problem in the given constraints this is not required.
The task “Mixing cards” was solved only by Eugene KAPUN
6) 2013, Qualifying Round, "E" Lasers
Parsing:
The main idea of the solution is a binary search by answer. Fix the maximum angle of deviation α and check the existence of a solution with such an answer. To do this, we reduce the problem to finding a path in the graph.
Denote the points given in the condition as P 1 , P 2 , ..., P n . Construct a graph of n (n - 1) vertices, where each vertex is an ordered pair of different points. Draw edges from a pair (i, j) into a pair (j, k) if the angle between the vectors P i P j and P j P k does not exceed α. In the constructed graph no more than n 3 edges. Now, if in such a graph there is a path from a vertex of the form (1, i) to a vertex of the form (j, 1), then with such α, the experiment can be carried out. You can check for the existence of a path using any path finding algorithm in the graph.
Thus, one iteration of the binary search works in O (n 3 ), which means that the whole algorithm can be implemented in O (n 3 log (1 / ε)) or, if we note that the search space is actually discrete (we are only interested no more than n 3 angles), then this algorithm can be implemented in O (n 3 log (n 3 )).
7) 2013, Final Round, “D” Robot
Parsing:
In this problem, it was necessary to find the expectation of the length of the shortest path from one corner of the field to another. At the same time, some cells of the field were painted white, and when the robot hit this cell, it was rearranged into a random white cell of the field.
Let us examine in more detail how the optimal strategy for choosing a path is arranged. For each cell of the field, you can calculate the expectation of the number of moves required to get into the right lower cell. In this case, the answer will correspond to the distance, which is recorded in the upper left cell. How to calculate these values? Consider a particular cell and all its neighbors. If the adjacent cell is colored black, then the answer for the cell will be at least (1 + value that is written in the adjacent cell). If the cell has a white neighbor, then the answer for it is at least (1 + arithmetic mean of responses for all white cells).
It is clear that if a robot gets in the same cell twice, then there is an optimal strategy in which the next move is the same in both cases. If this is not the case, then on some of the moves the robot did wrong and went into the cage with a great expectation of the number of moves to the end, which means that the strategy can be improved. There are two fundamentally different actions that a robot can do while in a certain cell. He can go immediately to the lower right corner of the black cells (if such a path exists), and he can go to some white cell. Obviously, among all the white cells in which you can go, you should choose the closest one.
For each cell, we calculate the distance to the lower right one by the black cells and the distance to the nearest white one. Note that for any white cell the distance to the nearest white one is not more than two. Now we divide all the white cells into two sets - those from which the robot must immediately go to the right lower cell, and those from which the robot must go to the next white one. When such a partition is made, the answer is easy to calculate. Writing the recurrence relation for the average response for all white cells, we find it. This will be some fraction with a denominator of no more than the number of white cells. Now the answer is min (the distance in black cells to the bottom right, the distance to the nearest white + the average answer for all whites).
It remains to learn how to find the correct division of white cells into sets. We sort all the white cells by the criterion (the distance to the right lower one by black - the distance to the nearest white one). It is argued that the optimal splitting is the following: from all cells of a certain prefix of a sorted array, it is necessary to go immediately to the right lower cell, and from the rest to the nearest white cell. This fact is easily proved by the opposite method (let the optimal partition have a different appearance; consider the average answer for white cells, we see that some cells can be moved from one set to another without worsening the answer, but reducing the partition to the desired form).
As a result, the decision boils down to the following. Calculate the distances discussed earlier for all cells. We sort the white cells. Let's sort the partition into sets, each time recalculating the average answer for white cells as O (1). The answer to the problem is the minimum from the distance in black cells and the distance to the nearest white cell + average answer for white cells. If you sort the white cells by counting, then the total complexity of the solution will be O (total number of cells).
Which of the tasks did you find most interesting?
The announcement of the first qualifying round on April 19.
We remind you in order to take part in the Russian Code Cup, you need to register on the site http://russiancodecup.ru/ (registration will be open before the start of the third qualifying round).
2011, Final Round, “B” Inverse Problem of the Bug
2011, Final Round, “D” Archiver
2012, 2nd qualifying round, “C” Tetrahedron
2012, Qualifying Round, "F" Prince
2012, Final Round, "E" Mixing the deck
2013, Qualifying Round, “E” Lasers
2013 Final Round, “D” Robot
')
1) 2011, Final Round, “B” Inverse Problem of the Bug
Parsing:
In this task, it was required for a given number k to build a maze in which the number of paths from the left upper to the lower right cell would be equal to k, provided that it is allowed to move only to the right and down.
Note the following. Suppose we have two mazes in which the number of ways to get from the top left to the right bottom cell is a and b, respectively.
Then, placing them in parallel, as shown in the figure, we can get a maze for which there are a + b ways to get from the top left to the bottom right cell. And placing them in series - get a maze in which ab paths.

Note that there are two paths in an empty 2 × 2 maze, and one path in a 1 × 1 maze. Therefore, by expanding the number k into a binary number system and using the method described, one can obtain a maze with k paths from the upper left to the right lower cell.
An example of such a maze for k = 19 is shown in the figure.

Note that for each digit of the number k, 5 cells are required horizontally, and 2 60 > 10 18 , therefore, the above scheme allows you to create a maze no larger than 300 × 300 in size, which is required in the condition of the problem.
2) 2011, Final Round, “D” Archiver
Parsing:
There are at least two different approaches to this problem: dynamic programming or a greedy algorithm.
Imagine the process of archiving a sequence in the form of a tree: each character of each of the intermediate sequences will be a vertex of the tree, the children of the vertex will be two characters that are “glued together” during the archiving process to the specified one. The original numbers are written in the leaves, and the task is to write down the numbers in all intermediate vertices, while the penalty for archiving is equal to the number of vertices that have different numbers in the children.
The solution using dynamic programming is arranged as follows: at each vertex u we will store the minimum total penalty p [u] [x] for the subtree if we write the number x at this vertex. Note that at the vertex it is sensible to write down only the number that occurs in one of the leaves in the subtree, so the total number of options that should be considered is O (n log n).
Recalculation is carried out as follows: consider the vertex u with children v and w. Suppose we plan to write the value of x. If both p [v] [x] and p [w] [x] are defined, then one of the options to put x in u is to put x in both children, the price of this option is p [v] [x] + p [w ] [x]. There is also an option to put x only in one child. Suppose we plan to put x in v, then the cost of this variant is p [v] [x] + minp [w] + 1, where minp [w] is the minimum value of p [w] [y] over all y.
An alternative solution to using DP is a greedy solution: for each vertex we will store a list of all possible values, putting one of which to the top we will get the minimum penalty in the subtree. It turns out that in order to find the optimal set for a vertex, it suffices to try to put only optimal values in its children. Moreover, if the lists of optimal values for children overlap, then you need to take one of these numbers. If they do not intersect, then any of the meanings of each of the children will do.
The proof of the correctness of the above algorithm is left as an exercise.
3) 2012, 2nd qualifying round, “C” Tetrahedron
Parsing:
Let me remind you that a tetrahedron is a polyhedron whose faces are four triangles (in other words, a triangular pyramid).
It all starts with the fact that we iterate over possible matches of matches to the edges of a tetrahedron. Denote the desired tetrahedron as ABCD. He has six edges: AB, AC, AD, BC, BD and CD. Let's go through all 6! = 720 variants, which match corresponds to which edge. Now it remains to verify that the corresponding tetrahedron exists.
How to check the existence of a tetrahedron? There are at least three solutions.
The first solution is based on the calculation of the volume of the tetrahedron. The simplest solution is to find a formula for calculating the volume of a tetrahedron over faces. This task is not an easy task by itself; here’s the formula:
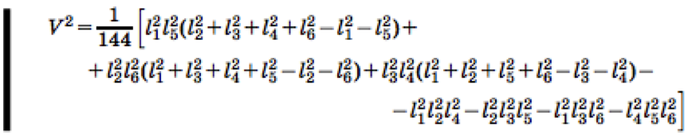
Accordingly, if the right-hand side of the equation turns out to be negative or the triangles in the faces cannot be constructed (triangle inequality), then the tetrahedron will not converge.
For those interested - here this formula is derived .
The second approach to solving the problem is geometric. First, make sure that ABC and BCD exist. Now try to make a tetrahedron. It is clear that when constructing a volumetric figure, a problem can arise only with the last edge - it can be either too long or too short. Therefore, this solution proposes to find the range of the length of the last edge.
There are two limiting ways of placing faces in which the tetrahedron turns into a flat figure. The first is when the faces are rotated 180 degrees relative to each other (CAB and CBD), and the second is when they are “folded” and form a “zero angle” (CA'D and CDB). All admissible positions of faces relative to each other are in the range between these boundary ones. The last edge (AD) reaches its greatest length in the first limiting variant (AD), and the smallest - in the last (A'D). Consequently, a tetrahedron will exist if this length of the last edge fits into the range found by us (from A'D to AD).
In order to find the distance between points A and D and A 'and D, we first find their coordinates, taking one of the common vertices for triangles as zero, and draw the abscissa axis through one of the edges emanating from this vertex. To find the coordinates of all the other vertices in this coordinate system is quite simple: through the aspect ratios and the cosines of the corners, we determine the vertex positions in polar coordinates (angle, distance), after which we translate them into a Cartesian coordinate system. Knowing the coordinates of the vertices, it is quite simple to calculate the maximum and minimum distances between unbound vertices.
The program should check whether the length of the remaining face fits in the specified ranges. If yes, then a tetrahedron of such lengths can be “assembled”.

The third way is also geometric. First you need to check the existence of all triangles with the specified sides. If at least one triangle cannot be built on the indicated values of the sides, then a tetrahedron cannot be built either. To verify it is necessary to check the inequality of a non-degenerate triangle: either of its sides must be strictly less than the sum of the two others.
In many cases, this decision was limited; Meanwhile, there are situations when triangles with specified sides can be constructed, and a tetrahedron cannot be assembled from them.
For example, if we have faces (100,100,2,101,100,2), then the triangles (100,100,2) and (101,100,2) formally satisfy the triangle inequality, but the tetrahedron of these triangles cannot be folded. From the figure we see that the edge AC is almost parallel to AB, which means that the distance from D to C will almost not change at any inclination of the face ABD relative to AB, from which we can conclude that DB is almost perpendicular to BC. In this case, the DC can be roughly estimated as the root of the sum of the squares of the legs, that is, the DC should be about 10, not at all 2, as we assumed in the condition.

Therefore, in addition to checking for triangles in the edges, it is necessary to perform an additional check for triangular angles. There are two necessary and sufficient conditions for the existence of a triangular angle:
- the sum of the flat corners of the triangular angle should be less than 360 degrees,
- each flat angle of the triangular angle should be less than the sum of the two other flat angles.
The plane angle is through the cosine theorem for the triangle.
In total, 1088 solutions were sent for verification, of which only 74 were correct (7%). 8% of participants of the Russian Code Cup QR2 coped with this task. The first decision came from a participant with the nickname AVictor 30 minutes after the start of the round.
4) 2012, Qualifying Round, "F" Prince
Parsing:
In this task, you need to find the minimum time during which the prince will get to the princess along a one-dimensional corridor, without falling into any trap. Known schedule, size and location of the appearance / disappearance of traps, as well as the speed of the prince. Since the corridor is one-dimensional, the prince can move either towards the princess, or from her, or not move anywhere at all. Obviously, there are situations where there is no way out, and the prince will not get to the princess - in this case, you need to withdraw Impossible.
The solution to this problem is to start by depicting traps on a plane, where the x coordinate is the position in the corridor and the y coordinate is the time. Now the problem can be reformulated in terms of this plane: you need to get from point (0, 0) to point (x, y) with minimum y, while it is allowed to move vertically up (stand still), diagonally right up and left up (move along the corridor) and it is forbidden to enter certain rectangles (traps). Being on the border of a rectangle is allowed.

The optimal path in such a task will consist of many parts of the same type, each of which will consist of moving along one of the diagonals to the coordinate corresponding to the border of one of the rectangles, followed by moving vertically up to the upper corner of this rectangle. Thus, the key points are the upper left and upper right corners of each rectangle, and you need to find out about them if you can get there.
When moving diagonally, we will support the set of rectangles above the current position. Since it is possible to be on the border of rectangles, we will not take into account rectangles that start or end at the current “corridor” coordinate. The rectangles will be stored in a set, ordered along the bottom edge. Such a set will be called a cut. For storing sets, you can use data structures like red-black or Cartesian trees or priority queues. The lower edge of the lower rectangle will be called the cut edge. If the slice does not contain rectangles, then we will consider its edge as infinity.
Since at any movement the time coordinate increases, we will consider the angles of the rectangles in the non-decreasing order of this coordinate. Considering the next angle, we will try to move from it diagonally in both directions. Movement is carried out according to the coordinates corresponding to the boundaries of the rectangles. Reaching the next coordinate, we check whether it is possible, moving vertically upwards, to get to the corresponding upper corner of some rectangle. You can reach the angle if this angle is not above the edge of the current slice. It is also necessary to check that the movement did not rest on the edge of one of the rectangles starting at the given coordinate. If you managed to reach the coordinates of the door x, then you need to update the current answer. If, when moving from one coordinate to another, the edge of the slice was exceeded, then at the transition the lower edge of the rectangle was reached, and the movement must be stopped.
Alternately examining all the angles and stepping in both directions from each of them, we find the minimum possible answer or information that the door is not reachable. The described algorithm performs O (n2 log n) operations, since it is necessary to pass from each of the O (n) angles along the O (n) diagonal of different coordinates and check the O (n) rectangles. Also, for each angle, it is necessary to perform O (n log n) operations in order to maintain the cutoff, since O (n) rectangles must be added and removed from the cutoff.
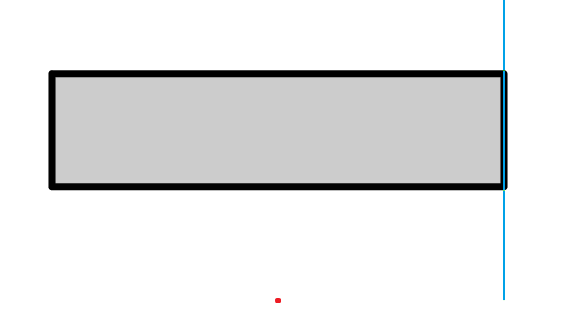
The following are possible options for passing by the rectangles that you need to remember to process.

and

At the same time on the next test it is impossible to have time to get to the door.

This task is also not an easy one - only 23 people decided it, the first was Kulikov Egor at 100: 18. It is worth noting Epifanov Vladislav, who sent the solution to this problem, the last for him, 2 minutes before the end of the tour. Vladislav won first place both in qualifying and in the qualifying round.
5) 2012, Final Round, “E” Mixing the deck
Parsing:
Sergey Melnikov , a student at NRU ITMO, tells about the task of mixing the deck.
In this task, you need to think about the mixing mechanism of the deck, which allows you to mix it ideally (that is, to make no two identical cards follow each other) for the minimum number of card block movements from the middle to the end of the deck. . Initially, the deck is sorted by non-decreasing dignity. Given the number of different advantages of cards, the order of cards in the deck, the number of decks.

Detailed statement of the problem
Let's call a conflict a situation in which two identical cards stand in a row:

We call the body the original sequence of cards, which we will gradually reduce by transferring the cards to the tail. The tail will be formed in such a way that the cards in it do not form conflicts.

Transform the original sequence into a sequence of conflicts and will work with the new sequence. We will call the color of the conflict the number written on the cards that form it. Each time transferring a piece of cards to the end of the deck, we will choose its ends inside the conflicts.
We denote the number of conflicts by K. Since one move operation removes no more than two conflicts, the task cannot be solved faster than in ⌈K / 2⌉ operations (here and later in the description there are constructions ⌊ ... and ⌈ ... ⌉ - these are rounding down and up respectively ).
Let M be the maximum number of conflicts of the same color and we will call these conflicts themselves “maximal”. We will learn how to solve the problem in the case when M = ⌈K / 2⌉.
Also I remind you that according to the conditions of the task the deck is sorted by non-decreasing value.
For example, in deck 1122333344, the number M will be equal to 3 (three conflicts 33), the total number of conflicts is 6. In this case, M = ⌈K / 2⌉.
In this case (not an example), there are two options:
- K is even (as in the example). Paint all the conflicts preceding the “maximum” in color A, the “maximum” conflicts in color B, and the subsequent ones in color C. | A | + | B | + | C | = | K |, therefore | A | + | C | = | B | = M. In the example above, the color coloring for 1122333344 would be AABBBC. We will eliminate conflicts in pairs: first the pairs (B, C), then when there are no such pairs left - the pairs (A, B). Note that the tail will have the form (B, C) * (A, B) *, where * is one or more repetitions. In our example, this is: 1122333344 (AABBC) -> 1122333-4.34 (AAB) -> 1-2333-4.3412 (BB) (hyphens denote the places where the cards were taken before being transferred to the tail. The point is the separator of the body and tail). Obviously, two conflicts of the same color do not go in a row. When mating with the body, everything will be fine too: if | C | > 0, then the last card with the value C will remain in place, and the tail will start with B. If | C | = 0, then the tail has the form (A, B) *, while the last card with the value B will remain in place.
- K is odd. Apply the same coloring. If there is at least one color card A, then we reduce the problem to the previous case, adding a virtual card and an A-conflict to the beginning. If there is a color card C, then we will add a new virtual card and a C-conflict to the end, again reducing to the previous case.
Solutions for these cases are optimal, since the lower bound of the number of operations ⌈K / 2⌉ is reached. So, we are able to solve the problem optimally, when the number of “maximum” conflicts is half of all conflicts (rounded up). We will call this case the base case.
Now we classify the initial situations by the maximum number of cards of the same denomination in a row. We will call these cards maximum and denote their number as Q.
- Q = 0. There are no conflicts, nothing needs to be done.
- If Q> ⌈N / 2⌉, then the problem has no solution. In this case, we have less than Q − 1 non-maximal cards, which is not enough to separate cards of maximum value.
- Q = ⌈N / 2⌉. In this case, there are not enough maximum cards, but every second card should be maximum. Having painted the cards in three colors we get:
- a A-cards reaching to the maximum,
- b = Q B-cards are the maximum
- c C-cards after the maximum.
- In this case, we will assume that all A- and C-cards form conflicts. Consider the following cases:
- a = 0. Therefore, c = N - Q = ⌊N / 2⌋, and then b differs from c by no more than one, that is, we have reduced it to the basic case.
- c = 0 . Similar to the previous case.
- a> 0, b> 0 Among A-cards a - 1 conflict, among B: b - 1, among C: c - 1. (a - 1) + (c - 1) = N - Q - 2, differs from Q - 1 is not more than one, which means that this is a basic case.
- M <⌊ (N + 1) / 2. If you can add a number of virtual conflicts (conflicts between cards with different values) so that the task is reduced to the base case, then we add them and solve them as the base case.
Now we will delete the last couple of conflicts each time, which can be removed (the last two conflicts of different colors) (C 1 , C 2 ). If in the process we get into the base case, then we will decide how we solve it. If no more conflicts remain, then the problem is solved.
We prove that new conflicts will not arise. Consider the color of the last conflict Z, we will transfer pairs of conflicts (X, Z) until Z ends, while Z remains at the end, and we get the tail Z (X 1 , Z) (X 2 , Z) .... If Z-conflicts end, then there will be a transition to (X, Y) conflicts, that is, a pair (X k , Z) (X k + 1 , Y), with X k + 1 Z.
In the transition to the basic case of conflict does not occur, because after the transfer of the pair (X, Z), neither X nor Z can become maximum (M). Since M ≠ Z, then either Z is over and there is no conflict (X, Z) (Z, ...), or Z is after M, that is, we get a continuation (X, Z) (M, Z).
Since we remove a couple of conflicts at each step, or use the base case, the constructed solution is optimal and works in “K / 2” operations.
You may notice that there is no need to store information about which numbers and in what order are written in the tail, since there are no conflicts there. The sequence of values can be maintained using a Cartesian tree using an implicit key, with the total running time being O (N log N). Also, if at some point we determine that there are no conflicts at the end of the body, then we can reduce the length of the body and, accordingly, increase the tail. It is possible to consider all cases when a segment moves, and make sure that the body will always look like: the prefix of the original array with no more than two subcut segments cut out. Based on this fact, it is possible to implement the solution in O (n), but to solve this problem in the given constraints this is not required.
The task “Mixing cards” was solved only by Eugene KAPUN
6) 2013, Qualifying Round, "E" Lasers
Parsing:
The main idea of the solution is a binary search by answer. Fix the maximum angle of deviation α and check the existence of a solution with such an answer. To do this, we reduce the problem to finding a path in the graph.
Denote the points given in the condition as P 1 , P 2 , ..., P n . Construct a graph of n (n - 1) vertices, where each vertex is an ordered pair of different points. Draw edges from a pair (i, j) into a pair (j, k) if the angle between the vectors P i P j and P j P k does not exceed α. In the constructed graph no more than n 3 edges. Now, if in such a graph there is a path from a vertex of the form (1, i) to a vertex of the form (j, 1), then with such α, the experiment can be carried out. You can check for the existence of a path using any path finding algorithm in the graph.
Thus, one iteration of the binary search works in O (n 3 ), which means that the whole algorithm can be implemented in O (n 3 log (1 / ε)) or, if we note that the search space is actually discrete (we are only interested no more than n 3 angles), then this algorithm can be implemented in O (n 3 log (n 3 )).
7) 2013, Final Round, “D” Robot
Parsing:
In this problem, it was necessary to find the expectation of the length of the shortest path from one corner of the field to another. At the same time, some cells of the field were painted white, and when the robot hit this cell, it was rearranged into a random white cell of the field.
Let us examine in more detail how the optimal strategy for choosing a path is arranged. For each cell of the field, you can calculate the expectation of the number of moves required to get into the right lower cell. In this case, the answer will correspond to the distance, which is recorded in the upper left cell. How to calculate these values? Consider a particular cell and all its neighbors. If the adjacent cell is colored black, then the answer for the cell will be at least (1 + value that is written in the adjacent cell). If the cell has a white neighbor, then the answer for it is at least (1 + arithmetic mean of responses for all white cells).
It is clear that if a robot gets in the same cell twice, then there is an optimal strategy in which the next move is the same in both cases. If this is not the case, then on some of the moves the robot did wrong and went into the cage with a great expectation of the number of moves to the end, which means that the strategy can be improved. There are two fundamentally different actions that a robot can do while in a certain cell. He can go immediately to the lower right corner of the black cells (if such a path exists), and he can go to some white cell. Obviously, among all the white cells in which you can go, you should choose the closest one.
For each cell, we calculate the distance to the lower right one by the black cells and the distance to the nearest white one. Note that for any white cell the distance to the nearest white one is not more than two. Now we divide all the white cells into two sets - those from which the robot must immediately go to the right lower cell, and those from which the robot must go to the next white one. When such a partition is made, the answer is easy to calculate. Writing the recurrence relation for the average response for all white cells, we find it. This will be some fraction with a denominator of no more than the number of white cells. Now the answer is min (the distance in black cells to the bottom right, the distance to the nearest white + the average answer for all whites).
It remains to learn how to find the correct division of white cells into sets. We sort all the white cells by the criterion (the distance to the right lower one by black - the distance to the nearest white one). It is argued that the optimal splitting is the following: from all cells of a certain prefix of a sorted array, it is necessary to go immediately to the right lower cell, and from the rest to the nearest white cell. This fact is easily proved by the opposite method (let the optimal partition have a different appearance; consider the average answer for white cells, we see that some cells can be moved from one set to another without worsening the answer, but reducing the partition to the desired form).
As a result, the decision boils down to the following. Calculate the distances discussed earlier for all cells. We sort the white cells. Let's sort the partition into sets, each time recalculating the average answer for white cells as O (1). The answer to the problem is the minimum from the distance in black cells and the distance to the nearest white cell + average answer for white cells. If you sort the white cells by counting, then the total complexity of the solution will be O (total number of cells).
Which of the tasks did you find most interesting?
The announcement of the first qualifying round on April 19.
Source: https://habr.com/ru/post/219567/
All Articles