Lock-free data structures. Another treatise

As you probably guessed, this article is devoted to lock-free queues.
Queues are different. They can differ in the number of writers (producer) and readers (consumer) - single / multi producer - single / multi consumer, 4 options - they can be limited (bounded, based on a predistributed buffer) and unlimited, based on a list (unbounded) , with or without priority support, lock-free, wait-free or lock-based, with strict adherence to FIFO (fair) and not very (unfair), etc. The types of queues are described in detail in this and this article by Dmitry Vyukov. The more specialized the requirements for the queue, the more efficient its algorithm, as a rule. In this article, I will look at the most common variant of queues — a multi-producer / multi-consumer unbounded concurrent queue without priority support.
The queue is perhaps the favorite data structure for researchers. On the one hand, it is simple
Classic lineup
A classic queue is a list (it doesn't matter if it is simply connected or biconnected) with two ends - Head and tail Tail. From the head we read, we write to the tail.
Naive standard queue
Copy-paste from the first article of the cycle
Do not look, there is no competition here - it’s just an illustration of how simple the subject for conversation is. In the article we will see what happens with simple algorithms, if they begin to adapt to a competitive environment.
UPD: thank you xnike , who first found a mistake here!
struct Node { Node * m_pNext ; }; class queue { Node * m_pHead ; Node * m_pTail ; public: queue(): m_pHead( NULL ), m_pTail( NULL ) {} void enqueue( Node * p ) { p->m_pNext = nullptr; if ( m_pTail ) m_pTail->m_pNext = p; else m_pHead = p ; m_pTail = p ; } Node * dequeue() { if ( !m_pHead ) return nullptr ; Node * p = m_pHead ; m_pHead = p->m_pNext ; if ( !m_pHead ) m_pTail = nullptr ; return p ; } }; Do not look, there is no competition here - it’s just an illustration of how simple the subject for conversation is. In the article we will see what happens with simple algorithms, if they begin to adapt to a competitive environment.
UPD: thank you xnike , who first found a mistake here!
The classic (1996) lock-free queue algorithm is considered to be the Michael & Scott algorithm.
As always, the
cds::intrusive::MSQueue . Comments are inserted by code, trying to make them not too boring. bool enqueue( value_type& val ) { /* Implementation detail: node_type value_type - , node_traits::to_node_ptr - static_cast<node_type *>( &val ) */ node_type * pNew = node_traits::to_node_ptr( val ) ; typename gc::Guard guard; // , , Hazard Pointer // Back-off (template- ) back_off bkoff; node_type * t; // lock-free, , ... while ( true ) { /* m_pTail, (delete) */ t = guard.protect( m_pTail, node_to_value() ); node_type * pNext = t->m_pNext.load( memory_model::memory_order_acquire); /* : , m_pTail , , . */ if ( pNext != nullptr ) { // ! //( ) m_pTail.compare_exchange_weak( t, pNext, std::memory_order_release, std::memory_order_relaxed); /* , CAS CAS — , m_pTail - , . */ continue ; } node_type * tmp = nullptr; if ( t->m_pNext.compare_exchange_strong( tmp, pNew, std::memory_order_release, std::memory_order_relaxed )) { // . break ; } /* — CAS . , - . — , — back_off */ bkoff(); } /* , — ... , - — , . , */ ++m_ItemCounter ; /* , m_pTail. , , — , , . '!' , dequeue */ m_pTail.compare_exchange_strong( t, pNew, std::memory_order_acq_rel, std::memory_order_relaxed ); /* true. , , bounded queue, false, . enqueue */ return true; } value_type * dequeue() { node_type * pNext; back_off bkoff; // dequeue 2 Hazard Pointer' typename gc::template GuardArray<2> guards; node_type * h; // , ... while ( true ) { // m_pHead h = guards.protect( 0, m_pHead, node_to_value() ); // pNext = guards.protect( 1, h->m_pNext, node_to_value() ); // : , , // ?.. if ( m_pHead.load(std::memory_order_relaxed) != h ) { // , - - ... // continue; } /* . , */ if ( pNext == nullptr ) return nullptr; // /* , Hazard Pointer' — , ( ) */ node_type * t = m_pTail.load(std::memory_order_acquire); if ( h == t ) { /* ! : , , . ... */ m_pTail.compare_exchange_strong( t, pNext, std::memory_order_release, std::memory_order_relaxed); // - // CAS continue; } // — // if ( m_pHead.compare_exchange_strong( h, pNext, std::memory_order_release, std::memory_order_relaxed )) { // — break; } /* ... , - . , */ bkoff() ; } // - , // . enqueue --m_ItemCounter; // ' h' dispose_node( h ); /* !!! ! , [] , pNext — ! */ return pNext; } As you can see, the queue is represented by a simply linked list from head to tail.
What is the important point in this algorithm? The important point is to contrive to control two pointers - on the tail and on the head - using the usual (not double!) CAS. This is achieved due to, firstly, the fact that the queue is never empty - look carefully at the code, is there somewhere head / tail
nullptr for nullptr ? .. You will not find. To ensure physical (but not logical) non-emptiness in the queue's constructor, one false (dummy) element is added to it, which is the head and tail. And the consequence of this is this: during the extraction ( dequeue ), an element is returned, which becomes the new dummy-element (new head), and the former dummy-element (former head) is deleted:')

This moment should be taken into account when constructing an intrusive queue — the returned pointer is still part of the queue and can only be deleted with the next
dequeue .Secondly, the algorithm explicitly assumes that the tail may not point to the last element. For every reading of the tail, we check whether it has the next element
m_pNext . If this pointer is not nullptr - the tail is not in place, you need to move it. There is another underwater stone here: it may happen that the tail points to the element in front of the head (the intersection of the head and tail). To avoid this, we implicitly check m_pTail->m_pNext : we read the head following the head element m_pHead->m_pNext , made sure that pNext != nullptr , and then we see that the head is equal to the tail. Consequently, there is something behind the tail, since there is a pNext , and the tail must be pushed forward. A typical example of mutual help (helping) flows, which is very common in lock-free programming.Memory ordering
I’m ashamed to hide such a confession behind the spoiler: the above code is not a model for the arrangement of memory ordering of atomic operations. The fact is that I did not see the detailed analysis of algorithms from the point of view of C ++ 11 memory ordering more complicated than the Treiber stack. Therefore, in this code, the memory ordering is placed rather by intuition, with a slight addition of the brain. Intuition is supported by a long-term run of tests, and not only on x86. I fully admit (and even suspect) that there are weaker barriers to this code, I remain open to discussion.
In 2000, a small optimization of this algorithm was proposed . It was noted that the
MSQueue algorithm in the MSQueue method at each iteration of the loop reads the tail, which is redundant: the tail needs to be read (to check that it is really a tail and points to the last element) only when the head has been successfully updated. Thus, we can expect a decrease in pressure on m_pTail under certain types of load. This optimization is represented in libcds by the class cds::intrusive::MoirQueue .Baskets queue
An interesting variation of
MSQueue was introduced in 2007. A rather well-known in lock-free circles researcher Nir Shavit and his comrades approached the optimization of the classic lock-free queue of Michael and Scott on the other hand.He presented the queue as a set of logical baskets (basket), each of which is available for adding a new element for some short period of time. The interval has passed - a new basket is being created.

Each basket is an unordered collection of items. It would seem that this definition violates the main property of the queue - FIFO, that is, the queue becomes not quite a queue (unfair). FIFO holds for baskets, but not for items in baskets. If the basket availability interval for adding is sufficiently small, we can neglect the disorder of the elements in it.
How to determine the duration of this interval? And it is not necessary to define it, the authors say Baskets Queue. Consider the
MSQueue . In the enqueue operation under high enqueue , when the CAS tail changes did not work, that is, where the back-off is called in MSQueue , we cannot determine in which order the elements will be added to the queue, as they are added simultaneously . This is the logical basket. In essence, it turns out that the abstraction of logical baskets is a kind of back-off strategy.I am not a fan of reading code kilometers in review articles, so I’ll not give the code. Using the example of
MSQueue we have already seen that the lock-free code is very verbose. Those wishing to see the implementation refer to the class cds::intrusive::BasketQueue library, file cds/intrusive/basket_queue.h . For the explanation of the algorithm, I will borrow another picture from the work of Nir Shavit & Co:
1. Threads A, B, C want to add items to the queue. They see that the tail is in its
MSQueue place (and we remember that in MSQueue tail may not indicate the last element in the queue at all) and try to change it at the same time .2. Stream A came out the winner - added a new element. Flows B and C losers - their CAS with a tail is unsuccessful, so they both start adding their items to the basket using the previously read old tail value.
3. Thread B was the first to add. At the same time, thread D also calls
enqueue and successfully adds its element, changing the tail.4. Thread C also successfully completes the addition. We look where he added - in the middle of the queue! When added, he uses the old pointer to the tail, which he read on entering the operation before performing his unsuccessful CAS.
It should be noted that with this addition it may well happen that the element will be inserted in front of the queue head. For example, the element in front of C in Figure 4 is above: while thread C is
enqueue on enqueue , another thread may already delete the element in front of C. To prevent such a situation, it is proposed to apply a logical deletion , that is, you must first mark the deleted elements with the special flag deleted . Since it is required that the flag and the pointer to the element itself can be read atomically, we will store this flag in the pNext bit of the pNext pointer of the element. This is permissible, since in modern systems memory is allocated evened out at least 4 bytes, so that the lower 2 bits of the pointer will always be zeros. Thus, we have invented marked pointers , which is widely used in lock-free data structures. This reception we will meet more than once in the future. By applying a logical deletion, that is, setting the low-order bit of pNext to 1 using CAS, we will exclude the possibility to insert an element in front of the head — the insertion is also performed by CAS, and the deleted element contains 1 in the low-order bit of the pointer, so the CAS will fail (of course when inserting, we take not all of the marked pointer, but only its high bits, which contain the actual address, the lower bit is set to zero).And the final improvement introduced by
BasketQueue concerns the physical removal of elements. It was noticed that changing the head with each successful call to dequeue can be costly - CAS is also called there, which, as you know, is rather heavy. Therefore, we will change the head only when several logically deleted elements have accumulated (in the default implementation of libcds three). Or when the queue becomes empty. It can be said that the head in BasketQueue changes by leaps (hops).All these optimizations are designed to improve the performance of the classic lock-free queue in a situation of high competition.
Optimistic approach

In 2004, Nir Shavit and Edya Ladan Mozes proposed another approach to optimizing
MSQueue , which they called optimistic .Warning
If anyone is interested in the original article - be careful! There are two articles of the same name — 2004 and 2008. The 2004 article gives some kind of furious (and seemingly inoperable) pseudo-queue code.
In the 2008 article, the pseudocode is different — pleasant for the eyes and working.
In the 2008 article, the pseudocode is different — pleasant for the eyes and working.
They noticed that in the Michael and Scott algorithm, the
dequeue operation requires only one CAS, whereas the enqueue two (see the figure to the right).This second CAS in enqueue can significantly affect performance even at low load, - CAS in modern processors is quite a hard operation. Is there any way to get rid of him? ..
Consider where in the
MSQueue::enqueue two MSQueue::enqueue came from. The first CAS associates a new element with a tail — changes pTail->pNext . The second - promotes the tail itself. Can the pNext field pNext changed with a regular atomic notation, and not with a CAS? Yes, if the direction of our simply linked list would be different - not from head to tail, but on the contrary, we could use an atomic store ( pNew->pNext = pTail ) to set pNew->pNext and then change pTail . But if we change direction, then how do dequeue do dequeue ? There will be no pHead->pNext , the direction of the list has changed.The authors of the optimistic lineup suggested using a doubly linked list.

There is one problem here: the effective algorithm for a doubly connected lock-free list on CAS is not yet known. Algorithms for DCAS (CAS over two different memory cells) are known, but there is no DCAS implementation in hardware. The MCAS emulation algorithm (CAS over M unrelated memory cells) is known on CAS, but it is inefficient (requires 2M + 1 CAS) and is more likely of theoretical interest.
The authors proposed this solution: the link in the list from tail to head (next, the link that is not needed for the queue, but the introduction of this link allows you to get rid of the first CAS in the
enqueue ) will always be consistent. But the feedback - from head to tail, the most important, prev - may be not quite consistent, that is, its violation is permissible. If we find such a violation, we can always restore the correct list by following the next links. How to detect such a violation? Very simple: pHead->prev->next != pHead . If this inequality is detected in the dequeue , the auxiliary fix_list procedure is fix_list : void fix_list( node_type * pTail, node_type * pHead ) { // pTail pHead Hazard Pointer' node_type * pCurNode; node_type * pCurNodeNext; typename gc::template GuardArray<2> guards; pCurNode = pTail; while ( pCurNode != pHead ) { // pCurNodeNext = guards.protect(0, pCurNode->m_pNext, node_to_value() ); if ( pHead != m_pHead.load(std::memory_order_relaxed) ) break; pCurNodeNext->m_pPrev.store( pCurNode, std::memory_order_release ); guards.assign( 1, node_traits::to_value_ptr( pCurNode = pCurNodeNext )); } } [Taken from the
cds::intrusive::OptimisticQueue class of the cds::intrusive::OptimisticQueue Library]fix_list runs through the entire queue from tail to head via the obviously correct pNext links and adjusts pPrev .Breaking the head-to-tail list (prev pointers) as soon as possible because of delays, and not because of a heavy load. Delays are a thread preemption by an operating system or an interrupt. Consider the code
OptimisticQueue::enqueue : bool enqueue( value_type& val ) { node_type * pNew = node_traits::to_node_ptr( val ); typename gc::template GuardArray<2> guards; back_off bkoff; guards.assign( 1, &val ); node_type * pTail = guards.protect( 0, m_pTail, node_to_value()); while( true ) { // — pNew->m_pNext.store( pTail, std::memory_order_release ); // if ( m_pTail.compare_exchange_strong( pTail, pNew, std::memory_order_release, std::memory_order_relaxed )) { /* — . (). pTail (dequeue) ( , pTail Hazard Pointer' , , ) */ pTail->m_pPrev.store( pNew, std::memory_order_release ); break ; // Enqueue done! } /* CAS — pTail ( CAS C++11: !) pTail Hazard Pointer' */ guards.assign( 0, node_traits::to_value_ptr( pTail )); // High contention - bkoff(); } return true; } It turns out that we are optimists: we build the
pPrev list (the most important for us), counting on success. And if then we find the forward and reverse list mismatches - well, we will have to spend time on reconciliation (launch fix_list ).So what's the bottom line? Both
enqueue and dequeue we now have exactly one CAS. Price - run fix_list when a list violation is detected. Big is the price or small - the experiment will say.The working code can be found in the
cds/intrusive.optimistic_queue.h , the cds::intrusive::OptimisticQueue class of the cds::intrusive::OptimisticQueue library.Wait-free queue
To end the conversation on the classic queue, it is worth mentioning the wait-free queue algorithm.
Wait-free is the most stringent requirement among others. It says that the execution time of the algorithm should be finite and predictable. In practice, wait-free algorithms are often noticeably (surprise!) Inferior in performance to their less strict counterparts — lock-free and obstruction-free — outperforming them in the number and complexity of the code.
The structure of many wait-free algorithms is rather standard: instead of performing an operation (in our case
enqueue / dequeue ), they first declare it, save the operation descriptor together with the arguments in some shared shared storage, and then begin to help competing threads: browse descriptors in the repository and try to accomplish what is written in them (descriptors). As a result, with a large load, several threads perform the same work, and only one of them will be the winner.The complexity of implementing such algorithms in C ++ is mainly how to implement this storage and how to get rid of memory allocation under descriptors.
The
libcds library libcds not have a wait-free queue implementation. For the authors themselves cite disappointing data on its performance in their research.Test results
In this article, I decided to change my dislike for comparative tests and present the results of testing the above algorithms.
Tests - synthetic, test machine - dual-processor Debian Linux, Intel Dual Xeon X5670 2.93 GHz, 6 cores per processor + hyperthreading, a total of 24 logical processors. At the time of the tests, the car was almost free - idle at 90%.
Compiler - GCC 4.8.2, optimization
-O3 -march=native -mtune=native .The queues to be tested are from the namespace
cds::container, that is, not intrusive. This means that memory is allocated for each element. We will compare with standard implementations std::queue<T, std::deque<T>>and std::queue<T, std::list<T>>with synchronization mutex. Type T- a structure of two integers. All lock-free queues are based on Hazard Pointer.Endurance test
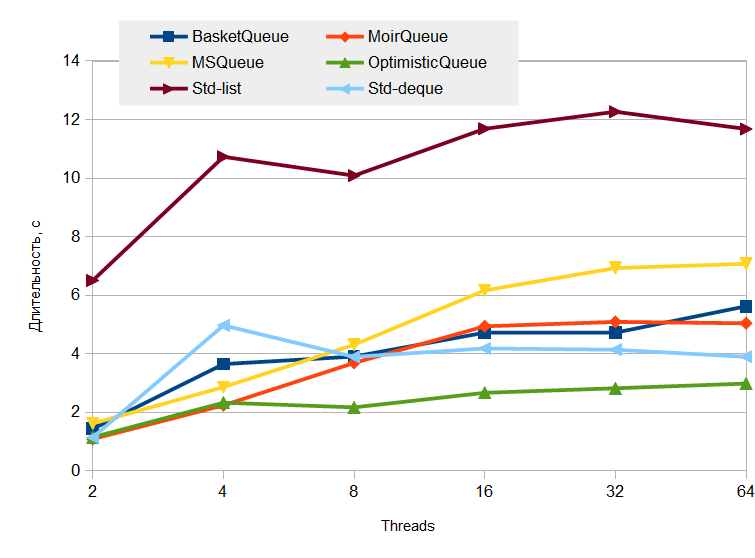
. 10
enqueue / dequeue . 10 enqueue , 75% — enqueue , 25% — dequeue ( 10 enqueue 2.5 — dequeue ). — dequeue 7.5 , .: , , , .
— :

What can I say? , —
std::queue<T, std::deque<T>> . Why? , : std::deque N , . , , , , , []. , libcds , , .lock-free , , ,
MSQueue , , .Prodcer/consumer test
. N N . 10 , , 10 . — .
— :
lock-free .
OpimisticQueue , — , , , ., — , ( ). , , — , , , , — .
—
…
lock-free
— producer/consumer: (
:
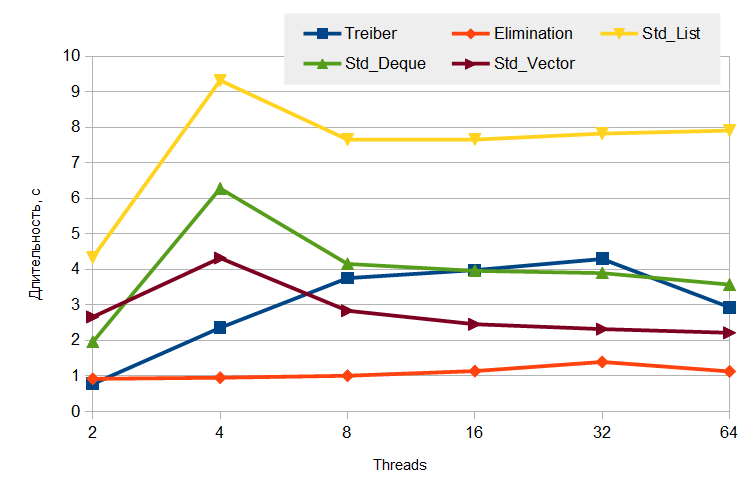
, .
, elimination back-off? , ,
lock-free
libcds elimination back-off Treiber'. , , / C++ (, , , — ). , elimination back-off, — . libcds .— producer/consumer: (
push ), — ( pop ). — , — . — 10 ( 10 push 10 pop ). .:

, .
, elimination back-off? , ,
push / pop . ( libcds , ), , 10 push/pop 10 – 15 ( 64 ), 0.1%, ( elimination back-off) 35 ! , elimination back-off , ( elimination back-off 5 ), .findings
, lock-free , . — . , . , .
, , lock-free, CAS - . , - , ( ), - .
« ».
To be continued…
Source: https://habr.com/ru/post/219201/
All Articles