OpenFOAM for dummies
Some time ago I was looking for a description of operations, processes occurring in the library of numerical modeling OpenFOAM. I found many abstract descriptions of the work of the finite volume method, classical difference schemes, and various physical equations. I also wanted to know in more detail - where did such values come from in such an output file at such and such an iteration, what expressions are behind these or other parameters in the fvSchemes, fvSolution settings files?
For those to whom it is also interesting - this article. Those who are familiar with OpenFOAM or with the methods implemented in it - write about the errors and inaccuracies found in the PM.
On Habré already had a couple of articles about OpenFOAM:
OpenFOAM in practice
OpenFOAM in terms of programmer physics
Therefore, I will not dwell on the fact that it is “an open (GPL) platform for numerical simulation, intended for simulation related to solving partial differential equations by the finite volume method, and widely used for solving problems of continuum mechanics.”
')
Today I am using a simple example to describe the operations that occur during the calculation in OpenFOAM.
So, given the geometry - a cube with a side of 1 meter:

We are faced with the task of simulating the flow-propagation of a certain scalar field (temperature, amount of matter), which is given by the following transport equation (1) within the volume of the body.
(one)
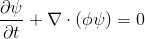 ,
,
Where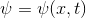 a scalar value, for example, expresses the temperature [K] or the concentration of a certain substance, and
a scalar value, for example, expresses the temperature [K] or the concentration of a certain substance, and  expresses substance transfer, mass flow [kg / s].
expresses substance transfer, mass flow [kg / s].
This equation, for example, is used to model the propagation of heat.
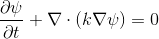 ,
,
where k is thermal conductivity, and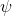 - temperature [K].
- temperature [K].
The boundary conditions of the problem are as follows: there is a face-entrance, a face-exit, the other faces are smooth walls.

Our grid will be very simple - we divide the cube into 5 equal cells along the Z axis.

The finite volume method provides that (1) in integral form (2) will be performed for each finite volume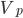 .
.
(2)
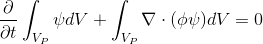 ,
,
Where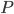 - the geometric center of a finite volume.
- the geometric center of a finite volume.
Simplify, transform the first term of expression (2) as follows:
(2.1) (HJ-3.12) *

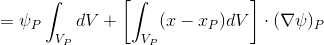
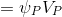
As you can see, we have assumed that the scalar quantity changes linearly within the final volume and the magnitude of at some point
at some point  inside the final volume can be calculated as:
inside the final volume can be calculated as:
(2.2)
 ,
,
Where
To simplify the second term of expression (2), we use the generalized Gauss-Ostrogradsky theorem : the integral of the divergence of a vector field by volume
by volume 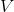 , is equal to the flow of the vector through the surface
, is equal to the flow of the vector through the surface 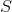 limiting this volume. In human language, "the sum of all streams to / from a finite volume is equal to the sum of streams through the edges of this finite volume":
limiting this volume. In human language, "the sum of all streams to / from a finite volume is equal to the sum of streams through the edges of this finite volume":
(2.3)
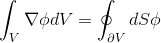 ,
,
Where closed surface limiting volume
closed surface limiting volume 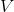 ,
,
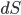 - vector directed along the normal from the volume
- vector directed along the normal from the volume  .
.
Taking into account that the final volume is limited by a set of flat edges, it is possible to transform expression (2.3) to the sum of integrals over the surface:
(2.4) (HJ-3.13)
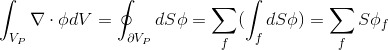 ,
,
Where expresses the value of the variable in the center of the face,
expresses the value of the variable in the center of the face,
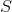 - vector of area, going out from the center of the face, directed away from the cell (locally), away from the cell with a smaller index to the cell with a larger index (globally).
- vector of area, going out from the center of the face, directed away from the cell (locally), away from the cell with a smaller index to the cell with a larger index (globally).
Not to store the same vector parameters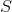 twice, because Obviously, for two neighboring cells, the vector-normal to the edge between the cells, directed away from the center of the cell, will differ only in the direction-sign. Therefore, the owner-neighbor relationship between the face and the cell was created. If the area vector
twice, because Obviously, for two neighboring cells, the vector-normal to the edge between the cells, directed away from the center of the cell, will differ only in the direction-sign. Therefore, the owner-neighbor relationship between the face and the cell was created. If the area vector 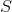 (global, positive direction from a cell with a smaller index to a cell with a large index) indicates FROM the center
(global, positive direction from a cell with a smaller index to a cell with a large index) indicates FROM the center 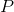 cells is the relationship between cell and vector
cells is the relationship between cell and vector 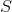 or, more precisely, between the cell and the edge, denoted by the owner). In case this vector
or, more precisely, between the cell and the edge, denoted by the owner). In case this vector 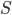 points inside the cell in question, then the neighbor relationship. The direction affects the sign of the magnitude (+ for the owner and - for the neighbor) and this is important when summarizing, see below.
points inside the cell in question, then the neighbor relationship. The direction affects the sign of the magnitude (+ for the owner and - for the neighbor) and this is important when summarizing, see below.

(HJ-3.16)
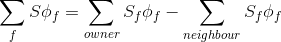
Value in the center of the face is calculated through the values
in the center of the face is calculated through the values  in the centers of adjacent cells - the method of such an expression is called the difference scheme. In OpenFOAM, the type of difference scheme is specified in the / system / fvSchemes file :
in the centers of adjacent cells - the method of such an expression is called the difference scheme. In OpenFOAM, the type of difference scheme is specified in the / system / fvSchemes file :
Gauss - means that the central difference scheme is selected;
linear - means that the interpolation from the centers of the cells to the centers of the faces will occur linearly.

Suppose that our scalar quantity varies linearly within the final volume from the center to the faces. Then the value approximated in the center of the face will be calculated according to the formula:
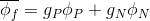
Where are the weights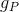 and
and 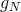 calculated as
calculated as
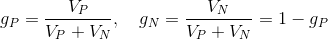
Where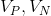 - the volume of cells.
- the volume of cells.
For cases of beveled cells, there are more complex formulas for calculating the weights of the approximation.
Thus, the values of phi_f at the centers of the faces of the cells are calculated based on the values at the centers of the cells. The grad (phi) gradient values are calculated based on the phi_f values.
And this whole algorithm can be represented as the following pseudocode.
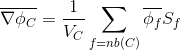
Considering (2.1) and (2.4), expression (2) takes the form:
(3)
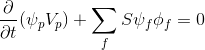
According to the finite volume method, time discretization is performed and expression (3) is written as:
(four)
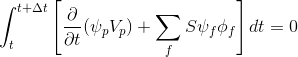
Integrating (4):
(4.1)
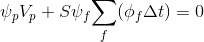
Divide the left and right side into :
:
(five)
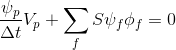
Now we can get a system of linear equations for each finite volume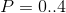 .
.
Below is the numbering of the grid nodes that we will use.

The numbering of the node-centers of the cells (50, 51 - the centers of the boundary faces):

Numbering of facet point centers:

The volume of items:
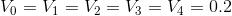
The interpolation coefficients required to calculate the values on the faces of the cells. The index "e" means "right edge of the cell." Right relative to the view, as in the figure “Numbering of node centers of cells”:
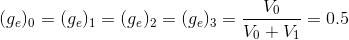
For P = 0.
Expression (5) describing the behavior of the quantity
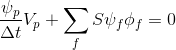
will be transformed into a system of linear algebraic equations, each of which of the form:
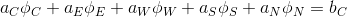
or according to indices of points on the edges
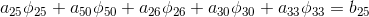
And all the flows to / from the cell can be expressed as a sum
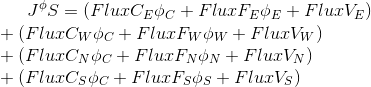
where for example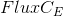 - the coefficient of linearization of the flow at the point-center of the cell E,
- the coefficient of linearization of the flow at the point-center of the cell E,
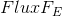 - the coefficient of linearization of the flow at the point-center of the face,
- the coefficient of linearization of the flow at the point-center of the face,
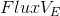 - nonlinear part (for example, a constant).
- nonlinear part (for example, a constant).
According to the numbering of faces, the expression will look like:
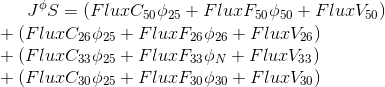
Given the boundary conditions for the element P_0, a linear algebraic equation can be represented as
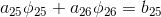
... we substitute the previously obtained coefficients ...
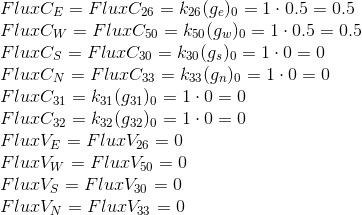
The flow from inlet'a is directed to the cell, therefore it has a negative sign.
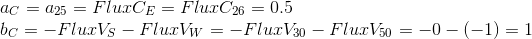
Since in our control expression there is, besides a diffusion term, a temporary term as well, but the final equation looks like
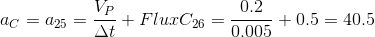
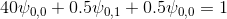
For P = 1.
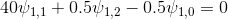
For P = 4.
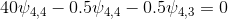
The system of linear algebraic equations (SLAE) can be represented in a matrix form as
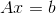 ,
,
Where
Further, the obtained SLAE is solved by the solver specified in fvSchemes .
And the result is a vector of values.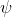
on the basis of which the values for the vector are obtained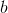
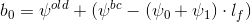
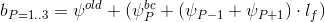

Then vector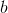 substituted in SLAU
substituted in SLAU 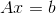 and there is a new iteration of the vector calculation
and there is a new iteration of the vector calculation  .
.
And so on until the residual reaches the required limits.
* Some equations in this article are taken from Yasak Hrvoe's dissertation (HJ is the equation number) and if anyone wants to read more about them ( http://powerlab.fsb.hr/ped/kturbo/OpenFOAM/docs/HrvojeJasakPhD.pdf )
Download task files here:
github.com/j-avdeev/case
Solver files:
github.com/j-avdeev/matrHyper1Foam
As a bonus - video, how the concentration spreads.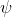 .
.
For those to whom it is also interesting - this article. Those who are familiar with OpenFOAM or with the methods implemented in it - write about the errors and inaccuracies found in the PM.
On Habré already had a couple of articles about OpenFOAM:
OpenFOAM in practice
OpenFOAM in terms of programmer physics
Therefore, I will not dwell on the fact that it is “an open (GPL) platform for numerical simulation, intended for simulation related to solving partial differential equations by the finite volume method, and widely used for solving problems of continuum mechanics.”
')
Today I am using a simple example to describe the operations that occur during the calculation in OpenFOAM.
So, given the geometry - a cube with a side of 1 meter:

We are faced with the task of simulating the flow-propagation of a certain scalar field (temperature, amount of matter), which is given by the following transport equation (1) within the volume of the body.
(one)
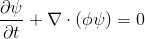 ,
,Where
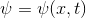 a scalar value, for example, expresses the temperature [K] or the concentration of a certain substance, and
a scalar value, for example, expresses the temperature [K] or the concentration of a certain substance, and  expresses substance transfer, mass flow [kg / s].
expresses substance transfer, mass flow [kg / s].This equation, for example, is used to model the propagation of heat.
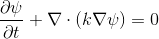 ,
,where k is thermal conductivity, and
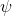 - temperature [K].
- temperature [K].Divergence operator is actually this
operator 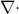 .
.
Let me remind you that there is an operator nabla (Hamilton operator), which is written as follows:
 ,
,
where i, j, k are unit vectors.
If we multiply the operator by a scalar by a vector value, we get the divergence of this vector:
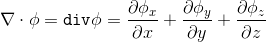
“From the point of view of physics, the divergence of a vector field is an indicator of the extent to which a given point of space is the source or sink of this field”
If we multiply the operator nabla by a scalar, we get the gradient of this scalar:
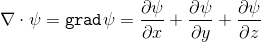
The gradient shows the increase or decrease in any direction of the magnitude of the scalar .
.
 .
.Let me remind you that there is an operator nabla (Hamilton operator), which is written as follows:
 ,
,where i, j, k are unit vectors.
If we multiply the operator by a scalar by a vector value, we get the divergence of this vector:
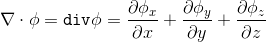
“From the point of view of physics, the divergence of a vector field is an indicator of the extent to which a given point of space is the source or sink of this field”
If we multiply the operator nabla by a scalar, we get the gradient of this scalar:
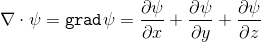
The gradient shows the increase or decrease in any direction of the magnitude of the scalar
 .
.The boundary conditions of the problem are as follows: there is a face-entrance, a face-exit, the other faces are smooth walls.

Splitting cube volume into finite volumes
Our grid will be very simple - we divide the cube into 5 equal cells along the Z axis.

Many formulas
The finite volume method provides that (1) in integral form (2) will be performed for each finite volume
 .
.(2)
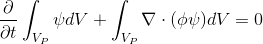 ,
,Where
 - the geometric center of a finite volume.
- the geometric center of a finite volume.Center of final volume

Simplify, transform the first term of expression (2) as follows:
(2.1) (HJ-3.12) *

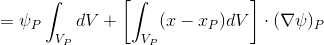
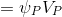
As you can see, we have assumed that the scalar quantity changes linearly within the final volume and the magnitude of
 at some point
at some point  inside the final volume can be calculated as:
inside the final volume can be calculated as:(2.2)
 ,
,Where

To simplify the second term of expression (2), we use the generalized Gauss-Ostrogradsky theorem : the integral of the divergence of a vector field
 by volume
by volume 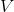 , is equal to the flow of the vector through the surface
, is equal to the flow of the vector through the surface 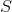 limiting this volume. In human language, "the sum of all streams to / from a finite volume is equal to the sum of streams through the edges of this finite volume":
limiting this volume. In human language, "the sum of all streams to / from a finite volume is equal to the sum of streams through the edges of this finite volume":(2.3)
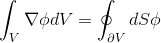 ,
,Where
 closed surface limiting volume
closed surface limiting volume 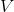 ,
,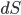 - vector directed along the normal from the volume
- vector directed along the normal from the volume  .
.S vector

Taking into account that the final volume is limited by a set of flat edges, it is possible to transform expression (2.3) to the sum of integrals over the surface:
(2.4) (HJ-3.13)
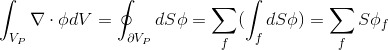 ,
,Where
 expresses the value of the variable in the center of the face,
expresses the value of the variable in the center of the face,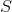 - vector of area, going out from the center of the face, directed away from the cell (locally), away from the cell with a smaller index to the cell with a larger index (globally).
- vector of area, going out from the center of the face, directed away from the cell (locally), away from the cell with a smaller index to the cell with a larger index (globally).A little more about the vector S
Not to store the same vector parameters
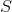 twice, because Obviously, for two neighboring cells, the vector-normal to the edge between the cells, directed away from the center of the cell, will differ only in the direction-sign. Therefore, the owner-neighbor relationship between the face and the cell was created. If the area vector
twice, because Obviously, for two neighboring cells, the vector-normal to the edge between the cells, directed away from the center of the cell, will differ only in the direction-sign. Therefore, the owner-neighbor relationship between the face and the cell was created. If the area vector 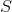 (global, positive direction from a cell with a smaller index to a cell with a large index) indicates FROM the center
(global, positive direction from a cell with a smaller index to a cell with a large index) indicates FROM the center 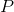 cells is the relationship between cell and vector
cells is the relationship between cell and vector 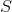 or, more precisely, between the cell and the edge, denoted by the owner). In case this vector
or, more precisely, between the cell and the edge, denoted by the owner). In case this vector 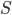 points inside the cell in question, then the neighbor relationship. The direction affects the sign of the magnitude (+ for the owner and - for the neighbor) and this is important when summarizing, see below.
points inside the cell in question, then the neighbor relationship. The direction affects the sign of the magnitude (+ for the owner and - for the neighbor) and this is important when summarizing, see below.
(HJ-3.16)
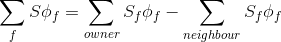
About difference schemes
Value
 in the center of the face is calculated through the values
in the center of the face is calculated through the values  in the centers of adjacent cells - the method of such an expression is called the difference scheme. In OpenFOAM, the type of difference scheme is specified in the / system / fvSchemes file :
in the centers of adjacent cells - the method of such an expression is called the difference scheme. In OpenFOAM, the type of difference scheme is specified in the / system / fvSchemes file :divSchemes { default none; div(phi,psi) Gauss linear; } Gauss - means that the central difference scheme is selected;
linear - means that the interpolation from the centers of the cells to the centers of the faces will occur linearly.

Suppose that our scalar quantity varies linearly within the final volume from the center to the faces. Then the value approximated in the center of the face will be calculated according to the formula:
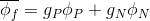
Where are the weights
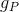 and
and 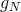 calculated as
calculated as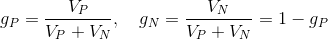
Where
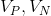 - the volume of cells.
- the volume of cells.For cases of beveled cells, there are more complex formulas for calculating the weights of the approximation.
Thus, the values of phi_f at the centers of the faces of the cells are calculated based on the values at the centers of the cells. The grad (phi) gradient values are calculated based on the phi_f values.
And this whole algorithm can be represented as the following pseudocode.
1. , 2. ( ) > flux_f = phi_f*S_f. phi_f phi > flux_f -owner -flux_f -neighbour 3. > flux_f = phi_f*S_f > flux_f -owner (neighbour- ) 4. > - Time discretization
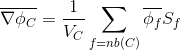
Considering (2.1) and (2.4), expression (2) takes the form:
(3)
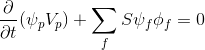
According to the finite volume method, time discretization is performed and expression (3) is written as:
(four)
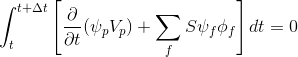
Integrating (4):
(4.1)
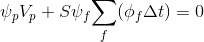
Divide the left and right side into
 :
:(five)
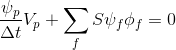
Data for the sampling matrix
Now we can get a system of linear equations for each finite volume
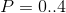 .
.Below is the numbering of the grid nodes that we will use.

The coordinates of the nodes are stored in / constant / polyMesh / points
24 ( (0 0 0) (1 0 0) (0 1 0) (1 1 0) (0 0 0.2) (1 0 0.2) (0 1 0.2) (1 1 0.2) (0 0 0.4) (1 0 0.4) (0 1 0.4) (1 1 0.4) (0 0 0.6) (1 0 0.6) (0 1 0.6) (1 1 0.6) (0 0 0.8) (1 0 0.8) (0 1 0.8) (1 1 0.8) (0 0 1) (1 0 1) (0 1 1) (1 1 1) ) The numbering of the node-centers of the cells (50, 51 - the centers of the boundary faces):

Numbering of facet point centers:

The volume of items:
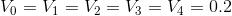
The interpolation coefficients required to calculate the values on the faces of the cells. The index "e" means "right edge of the cell." Right relative to the view, as in the figure “Numbering of node centers of cells”:
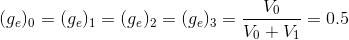
Forming a discretization matrix
For P = 0.
Expression (5) describing the behavior of the quantity
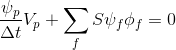
will be transformed into a system of linear algebraic equations, each of which of the form:
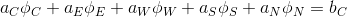
or according to indices of points on the edges
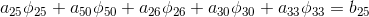
And all the flows to / from the cell can be expressed as a sum
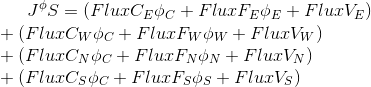
where for example
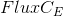 - the coefficient of linearization of the flow at the point-center of the cell E,
- the coefficient of linearization of the flow at the point-center of the cell E,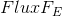 - the coefficient of linearization of the flow at the point-center of the face,
- the coefficient of linearization of the flow at the point-center of the face,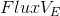 - nonlinear part (for example, a constant).
- nonlinear part (for example, a constant).According to the numbering of faces, the expression will look like:
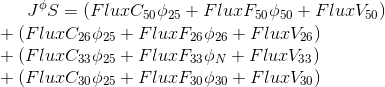
Given the boundary conditions for the element P_0, a linear algebraic equation can be represented as
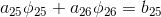
... we substitute the previously obtained coefficients ...
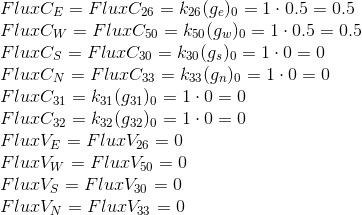
The flow from inlet'a is directed to the cell, therefore it has a negative sign.
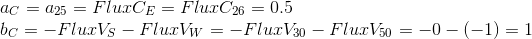
Since in our control expression there is, besides a diffusion term, a temporary term as well, but the final equation looks like
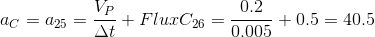
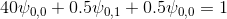
For P = 1.
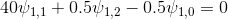
For P = 4.
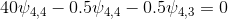
The system of linear algebraic equations (SLAE) can be represented in a matrix form as
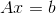 ,
,Where
=== A(i,j) === 40.5 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40.5 === b(i,j) === 1 0 0 0 0 Further, the obtained SLAE is solved by the solver specified in fvSchemes .
And the result is a vector of values.
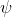
psi = dimensions [0 0 0 0 0 0 0]; internalField nonuniform List<scalar> 5(0.0246875 0.000308546 3.85622e-06 4.81954e-08 5.95005e-10); on the basis of which the values for the vector are obtained
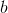
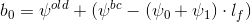
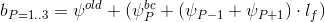

Then vector
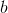 substituted in SLAU
substituted in SLAU 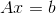 and there is a new iteration of the vector calculation
and there is a new iteration of the vector calculation 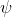 .
.And so on until the residual reaches the required limits.
Links
* Some equations in this article are taken from Yasak Hrvoe's dissertation (HJ is the equation number) and if anyone wants to read more about them ( http://powerlab.fsb.hr/ped/kturbo/OpenFOAM/docs/HrvojeJasakPhD.pdf )
Download task files here:
github.com/j-avdeev/case
Solver files:
github.com/j-avdeev/matrHyper1Foam
As a bonus - video, how the concentration spreads.
 .
.Source: https://habr.com/ru/post/218483/
All Articles