Functional image processing in D

Recently, I completed the reworking of a graphics package for my D library. Inspired by the std.algorithm and std.range modules , I tried to achieve the following goals:

• Present all in the form of small combinable components.
• Avoid implicit copying and preferably use lazy calculations.
• Use templates to improve the performance and efficiency of writing code.

Starting from the first version, all components of the image processing package have been parameterized by the color type. This is not a standard way of implementing graphic libraries - most abstract a particular type of image color through an OOP interface, or simply convert all images into a single pixel format, which they later work with in memory. However, in most cases this is a waste of memory and time, usually the developers know in advance what format the image will be presented, with the exception of applications where graphic data are entered by the user (for example, graph. Editors). Instead, my library declares all types of images as templates with a parameter type for color.
')
I am very pleased with the results of the work on the library, so I want to share a few interesting points in this post.

---

The library begins with a view definition:

///  ,    width, height ///       ///    enum isView(T) = is(typeof(T.init.w) : size_t) && // width is(typeof(T.init.h) : size_t) && // height is(typeof(T.init[0, 0]) ); // color information 

This method of declaring static interfaces is the same as used in std.range, for example, isInputRange . Instead of declaring an interface that is close in meaning to OOP, static interfaces in D are conditionally determined using a test for the implementation of certain features (note trans. Duck typing ). The check succeeds if the operations that the type must implement are compiled without errors or have a specific type. Usually, IsExpression or trait compiles is used for this.

Similarly, std.range.ElementType we define a template to get the type that is used in the view for the pixel color:

 ///     view alias ViewColor(T) = typeof(T.init[0, 0]); 

Next, we define several specializations for the view:


Again, this is similar to the definition of isForwardRange : a check that the type implements all the basic features, as well as some additional features specific to this specialization.

Since the implementation of direct access to the pixels can be defined through the scanline direct view, we declare the template mixin that implements it:


For example, define an Image template that describes an image in memory:


Arrays in D are implemented through a pointer and length (and only request memory when they are expanded or glued together), so the expression pixels [w * y ... w * (y + 1)] does not create a copy of the array.

The unit test checks at compile time that the Image actually satisfies the conditions of the isDirectView interface:

 unittest { static assert(isDirectView!(Image!ubyte)); } 

---

So, what can we do with this model?

First, we can define images that do not actually refer to an array of pixels, but instead calculate them on demand:


This template of the same name uses std.functional.binaryFun to convert a string (which will be mixed in ) into a predicate, or delegate (lambda). Since the function has a return type of auto and returns a struct declared inside this function, Procedural is an example of Voldemort types .

The simplest example of a procedural image filled with one color:

 ///  view,   ///     auto solid(COLOR)(COLOR c, int w, int h) { return procedural!((x, y) => c)(w, h); } 

Notice how the color type of the returned view is derived from the parameter type c, so solid (RGB (1, 2, 3), 10, 10) will return the view from the RGB pixels, even if it does not have a fully qualified name.

---

Another thing that can be represented in this model is creating views that transform other views in various ways. Define another template mixin for frequently used code:


Let's look at the static if (isWritableView! V) line , which says that the view [x, y] = c operator should be defined only if the underlying view supports it. Total wraped view will be changeable only if the underlying view can also be changed.

Using this function, we can define a cropping view , which represents a rectangular piece of another view:


if (isView! V) template constraint checks that the first argument matches the conditions of the isView interface.

As before, crop uses isDirectView to provide direct access to the pixels, if the underlying image supports it. Direct access to the pixels is useful when working with a large number of pixels at a time, which leads to an increase in performance compared to sequential access. For example, when copying one image to another, it is much faster to use slice copies (a type-safe replacement of memcpy in D), than to assign the values ​​of each pixel independently:


The same idea as in crop can be used to implement a view that tails another view or scales according to the nearest-neighbor algorithm (scaling algorithms are more complicated and better implemented in the imperative style). The code is very similar to crop , so I don’t include it here.

Even if crop takes a source as a normal argument, the intended use of this function and others like it is as if it is a method of the original view: someView.nearestNeighbor (100, 100) .tile (1000, 1000) .crop (50, 50, 950, 950) . This feature is due to a feature of the language called “Uniform Function Call Syntax” (or simply UFCS), which allows you to write a.fun (b ...) instead of fun (a, b ...) . The main advantage of this feature is the possibility of organizing chaining ( a.fun1 (). Fun2 (). Fun3 () instead of fun3 (fun2 (fun1 (a))) ), which is used to the full extent in Phobos and in this package.

---

For simple transformations in which the size of the view does not change, we can define an auxiliary function that simplifies the application of a user-defined formula to each pixel coordinate:


warp uses a clever method of checking formulas. The testWarpY function is declared as a template, however with zero template arguments. This forces the compiler to not conduct a semantic analysis of the body of this function until its use. And since it does not have x in scope, it can be successfully installed only if yExpr does not use x . The expression __traits (compiles, testWrapY ()) checks for this. All this allows us to determine the direct view scanline only if we are sure that we can do it safely. Example:


The q {...} syntax is simply a convenient way to define string constants. This entry is usually used for D code, which is then mixed somewhere. The expression has access to all characters in the place of mixing - in our case, this is the warp function and the testWarpY method of the Wrapped structure.

Since vflip satisfies the first two conditions necessary to declare the scanline method, someView.vflip () will be a direct view, if someView is . And this was achieved without explicit verification for the vflip ad.

Since the abstraction used does not rely on dynamic polymorphism, the compiler is free to embed calls to all layers of transformations. Inverting the image does not generate the operation twice, and, in fact, i [5, 5] and i.hflip (). Hflip () [5, 5] generate the same machine code. Compilers D with a more advanced backend can perform even more aggressive optimizations: for example, if you define the flipXY function, which inverts the X and Y axes, and rotateCW (to rotate an image 90 ° counterclockwise) as src.flipXY (). Hflip () , then four successful rotateCW calls are cut during optimization.

---

Let's move on to the operations on the pixels themselves. The main function in std.algorithm is map , which returns a range that lazily applies an expression over another range. Our colorMap uses this idea for colors:


Using colorMap , defining a function that inverts the colors of an image is as simple as:

 alias invert = colorMap!q{~c}; 

colorMap does not require matching the source and result color types. This allows you to use it for color conversion: read ("image.bmp"). ParseBMP! RGB (). ColorMap! (C => BGRX (cb, cg, cr)) returns RGB as BGRX view.

---

Image processing very often lends itself well to parallelization . std.parallelism helps to make the task of parallel image processing trivial:

Even if parallel shares its name with those functions that are present in std.parallelism , there is no conflict, as they have different signatures and work on different types.

At the same time, the operation can be divided between several streams by replacing image.process () with image.parallel! (Segment => segment.process ()). Vjoin () .

---

Practical examples:

• Creating a short animation:
  
  Code

   import std.algorithm; import std.parallelism; import std.range; import std.stdio; import std.string; import ae.utils.geometry; import ae.utils.graphics.color; import ae.utils.graphics.draw; import ae.utils.graphics.gamma; import ae.utils.graphics.image; void main() { enum W = 4096; const FG = L16(0); const BG = L16(ushort.max); auto image = Image!L16(W, W); image.fill(BG); enum OUTER = W/2 * 16/16; enum INNER = W/2 * 13/16; enum THICK = W/2 * 3/16; image.fillCircle(W/2, W/2, OUTER, FG); image.fillCircle(W/2, W/2, INNER, BG); image.fillRect(0, W/2-INNER, W/2, W/2+INNER, BG); image.fillRect(W/2-THICK/2, W/2-INNER, W/2+THICK/2, W/2+INNER, FG); enum frames = 32; foreach (n; frames.iota.parallel) image .rotate(TAU * n / frames, BG) .copy .downscale!(W/16) .lum2pix(gammaRamp!(ushort, ubyte, ColorSpace.sRGB)) .toPNG .toFile("loading-%02d.png".format(n++)); } 

  
  
  
  
  This program draws the original image in higher resolution, using a 16-bit brightness, which then converts it into an 8-bit sRGB image after reduction. Zooming out avoids aliasing , and color conversion is necessary for accurate resizing .
  
  This is what happened after converting PNG frames to GIF: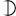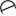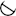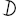
  
  
• Drawing a gray-white image of the Mandelbrot set :
  
  Code

   auto mandelbrot(int w, int h) { import std.algorithm, std.range; import ae.utils.graphics.view; return procedural!((x, y) { auto c = (2.0*x/w - 1.5) + (2.0*y/h - 1.0)*1i; return cast(ubyte)(1+ recurrence!((a, n) => c + a[n-1]^^2)(0+0i) .take(ubyte.max) .countUntil!(z => z.re^^2 + z.im^^2 > 4)); })(w, h); } void main() { import std.stdio; import ae.utils.graphics.image; mandelbrot(500, 500).toPNG().toFile("mandel.png"); } 

  
  
  
  
  This program uses recurrence , take and countUntil primitives over the D ranges, as well as built-in support for complex numbers, allowing you to concisely implement an algorithm that usually requires many lines to implement (However, the built-in complex numbers are now in the process of being obsolete in favor of std.complex ).
  
  Result of work:
  
  Picture

  
  
  
  

---

The template approach promises big performance gains. As a simple benchmark, this program reduces the scale of all images in the directory by 25%:


I compared the result of the work with the equivalent ImageMagick team:

 convert \ input/*.bmp \ -depth 16 \ -gamma 0.454545 \ -filter box \ -resize 25% \ -gamma 2.2 \ -depth 8 \ output-im/%02d.bmp 

Version on D runs 4-5 times faster. Of course, this is an unfair comparison: even if both use 16-bit color depth, gamma correction, multithreading and are optimized for the same architecture, the D program contains code specially optimized for this task. If you do not take into account the various JIT technology, the package can not be compared with libraries of image processing, general purpose.

---

A graphics package is available on GitHub . Thanks to David Ellsworth for his contribution to this article.