Symmetry numbers
Symmetry numbers
1. Introduction
In our world, everything is interconnected, it seems to each other, it has the same or similar parameters. Often these properties are called symmetry. In the "Concise Oxford Dictionary", symmetry is defined as "Beauty due to the proportionality of body parts or any whole, balance, similarity, harmony, consistency." [1] Very often, symmetry manifests itself in mathematics and physics. In physics, the properties of symmetry are clearly manifested in quantum mechanics and its mathematical apparatus, for example, the Schrödinger equation [2]. In mathematics there is a special mathematical apparatus, operating with the concepts of similarity and symmetry. This mathematical apparatus is called group theory [3]. One of the practical applications of symmetry in mathematics is RSA public key encryption [4].
2. Matrix of residuals of a prime number
Consider the definition of deduction and comparison by module. Here is the definition given in the modern explanatory dictionary. The number “a“ is called the residue of the number “b“ modulo “m“ if the difference “a - b“ is divided by “m“ (a, b, m> 0 are integers). That is, “a“ is comparable to “b“ modulo “m“.
a ≡ b (mod m)
')
This means that if “a“ is not completely divided by “m”, then “b“ is the remainder of dividing “a“ by “m“. Two integers “a“ and “b“ are comparable modulo a natural number “m“ if they give identical residues when divided by “m“.
Take a simple integer and denote it by “b”. The set of integers in the interval (1,2,3, ... b-1) is denoted by “B“. If this set is written in the form of a column, in ascending order from bottom to top, then we get the matrix column. All numbers in this column are arranged one after another, their number is equal to “b - 1“. Denote this column by the number “1“. Each number from the set “B“ is squared and divided by “b“ with the remainder. The resulting remnants of the remainder will write in the column. Denote this column by the number “2“ and place it to the right of column number “1“. It is necessary to arrange the remains so that they correspond to the numbers squared, and are with them in one straight line. After that, we will raise each number from the set “B“ to the third degree and divide it by “b“ with the remainder. From the obtained residues, we form a column with the number “3“, by analogy with column number “2“. Further, by analogy, we raise to the next degree and find the remains of division by “b“. We perform actions as long as the exponent in which we build numbers from the set “B“ is less than “b“. As a result, we obtain a square matrix of size (b-1) x (b-1).
An example of such a square matrix for a prime integer “b = 23” is shown in Fig.1.
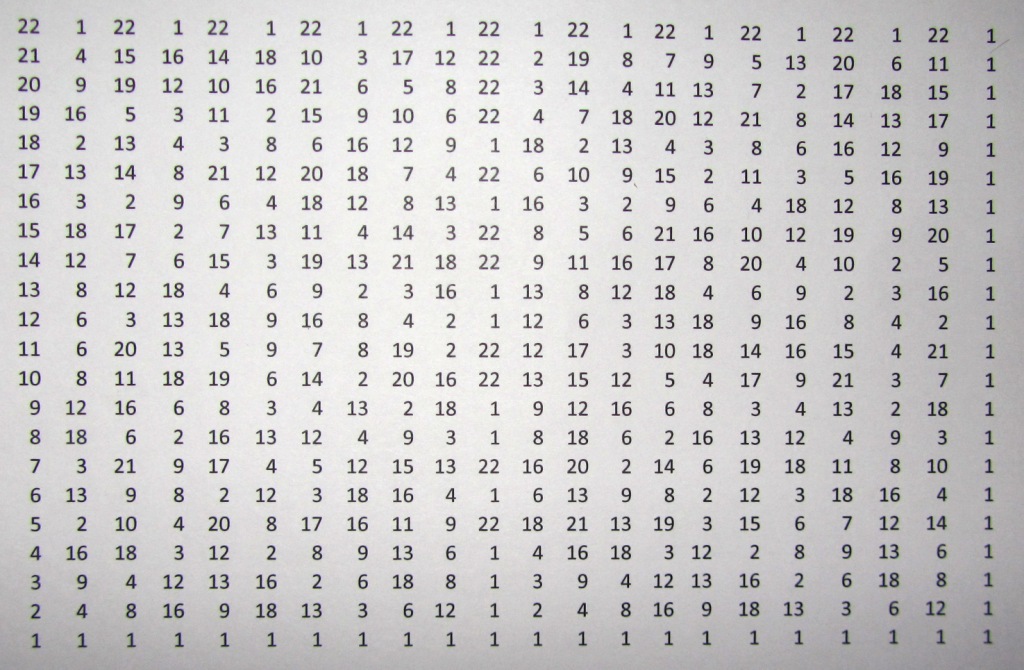
Fig. 1 Matrix of residuals of a simple integer b = 23.
The resulting matrix has amazing properties:
- It is clearly seen that the last column of the matrix consists of one units. This is fully consistent with the Farm simplicity test. A n-1 ≡ 1 (mod N) [5].
- It should be noted that the column with the number (b-1) / 2 (“b“ minus 1 divided by 2) consists of only two values of the set “B“. These are the values 1 and (b-1).
- The values of the numbers, the sets “B“, in the columns are symmetrical about the middle of the interval, i.e. value pairs (b-1) / 2 and (b + 1) / 2.
- The types of symmetry for different columns are different.
- For columns with even numbers, the values are equidistant from the middle of the interval, i.e. the pairs of values (b-1) / 2 and (b + 1) / 2 are the same. For the matrix shown in Fig. 1, the remainder of 11 squared divided by 23 and the remainder of 12 squared divided by 23 are equal and equal to 6.
- For columns with odd numbers, the values equidistant from the middle of the interval, i.e. The value pairs (b-1) / 2 and (b + 1) / 2 are always equal to “b“. For the matrix shown in Fig. 1, the remainder of 11 in the third degree, divided by 23, is 20, the remainder of 12 in the third degree, divided by 23, is 3. In total, these two residues are 23, i.e. are equal to “b“.
All properties described above and considered for the matrix shown in fig. 1, are inherent in matrices constructed according to the same rules for other simple integers.
3. Matrix residual composite number
The matrix considered in Section 2 characterizes the symmetry of primes. For composite numbers, the matrix constructed by the same rules is significantly different. It inherits the properties of the matrix of a prime number, but acquires new properties. Consider a composite number that is a product of two primes “x“ and “y“. Similarly, the value of a number is denoted by “b“, and the set of all numbers in the interval (1, b-1) is denoted by “B“. Consider the composite number “b = 35“, which is the result of multiplying the primes “x = 5“ and “y = 7“. We construct a matrix of residues of various degrees for the numerical interval (35-1). The residual matrix is shown in Fig. 2

Fig. 2 Residual matrix of composite number b = 35.
Some properties are inherited from the matrix of residues of a prime number. For example, the values of the numbers present in the columns are symmetric about the middle of the values of the numerical interval, i.e. values (b-1) / 2 and (b + 1) / 2.
The matrix shown in Fig. 2, bears in itself new properties:
- The values of the rows of the matrix, in which the first column contains multiples of divisors of a composite number, take numerical values of multiples of the divisors of a composite number and are never equal to 1. For example, in the matrix of Fig. 2, row 5, in the second column, has the value 25, in the third 20, in the fourth 30 and so on. All these values are multiples of 5.
- If we exclude rows whose values are multiples of the divisors of the number “b“, then there will necessarily be two columns in which the remaining values are 1. For example, in fig. 2 are columns with numbers 12, 24.
- Of these two selected columns, the largest column number is the product (x-1) by (y-1). Those. if from each of the factors, subtract 1 and multiply them, then we get the number of the largest selected column. For the matrix in fig. 2 factors of the number “b“ are 5 and 7. If we subtract 1 from each of them and multiply, we get (5-1) x (7-1) = 24. This is exactly the number of the largest selected column. It should be noted that in this case, the column number is equal to the Euler function, whose value is (x-1) x (y-1) = (n). [6].
- The second column must contain four values equal to 1. For the matrix of residues of a prime number and the values of the set “B” equal to (1, b-1), the values in the second column take the value 1. For the matrix of residues of a composite number, there are two more numbers the sets “B“, in the case of which they are squared and divided by “b“, the remainder is 1. In Fig. 2 are numbers 6 and 29.
- There are always pairs of numbers, sets “B“, following each other, the values of which are multiples of the divisors “x” and “y” of the number “b”. For the matrix in fig. 2 are pairs (14, 15) and (20, 21).
All properties described above and considered for the matrix shown in fig. 2, are inherent in matrices constructed according to the same rules for other composite integers.
4. Factoring numbers
If we consider the RSA public key encryption method [4], then its use is based on the existence of mutually opposite mappings in the matrix of residuals of a composite number. If we take the composite number “b“, there are always two columns “c“ and “d“ in its residue matrix, for which the following conditions are true:
(b1 ** c) ≡ c1 (mod b); (c1 ** d) ≡ d1 (mod b); b1 = d1
where b1, c1, d1 are numeric values in columns 1, c, d.
That is, for the composite number “b“ there always exist two numbers “c“, “d“ from the range (1, b-1) for which the sequence of actions is valid:
- We define the remainder of any number “b1“ from the range (1, b-1) raised to the power of “c“ and divided by “b“. We denote this remainder by “c1“.
- The resulting residue “c1“ will be raised to the power of “d“ and divided into “b“ with the remainder. We denote this remainder by “d1“.
- The resulting residue “d1“ is always equal to “b1“.
For the RSA encryption algorithm, (c, b) is the public key, (d, b) is the secret key.

Fig. 3 Residual matrix of the composite number b = 33.
Consider the matrix of residuals of the number b = 33, fig. 3. For this number c = 3, d = 7. Take any number from the first column, for example, 8 and raise it to the 3rd power, the remainder is 17. We raise 17 to the power 7, the remainder is 8, i.e. this remainder is equal to the original number from the first column.
RSA is one of the common public key encryption algorithms. Together with the improvement of encryption methods, methods for decrypting secret messages are being improved.
Often, the decryption task for RSA is attempted in the forehead, i.e. find the divisors of the base composite number. These methods are called factorization of numbers. In addition to a simple enumeration of values and verification of numbers, use the quadratic sieve method.
The basis of this method is that part of the residuals from squaring and dividing by the number “b“ are full squares of numbers. In fig. 2 full squares are the quadratic residues of the numbers (11, 12, 17), from the first column. To find the divisors of the number “b“, it is necessary to extract the square root from the quadratic remainder. The result, i.e. square root, subtract from the number “b“ or add to the number “b“. Multiple divisors of the number “b” will be obtained. Using the Euclidean algorithm, one can find the divisors of the number “b“.
In fig. 2, for the number 11, the quadratic remainder is 16. We extract the square root of 16, it is 4. We add 4 to 11, we get 15, a multiple of the divisor 5. We take 4 from 11, we get 7, the number is equal to 7.
One of the most modern methods of factoring numbers is the sieve method of a number field [7]. This method allows reducing the number of values to be checked and reducing the time for performing calculations. The use of the sieve method of the numerical field and the properties of the matrix of residuals of the composite number makes it possible to achieve even more powerful results.
For experimental verification of the methods of factorization of numbers, you can use the so-called Mersenne numbers [8]. These numbers are the number 2 to the power of “n“, minus 1, where the “n“ is a natural number. Only a limited number of Mersenne numbers are simple; the rest are decomposed into a finite number of divisors.
As an illustrative example, one of the divisors, the number 2 to the power of 4099, minus 1, is equal to -
431654595928296534254101974033397155588925169723783332084380283993261
209600632883153055473166663136594966053411838575253500155337120152873
781979635198920643526624304319945635699208877607737201529464080041890
547345467573782661041054825447947267620282789541695832747170633177331
920343746996221855049648583763367504662477325712779883313257418325242
923223374882540094860518718525171060169694349915604794431233943848839
032331927197514745282594881581533286782002526616104836932259305133211
436643050243706215479754994805351437606942854754835739144357537526269
041212016993538655106720507482318994547865735219931202814880677303379
021540170667630675512896640229254326407201860556265718380698467494757
374722667518146123812589844575734597771351069823560862537030159862538
798769879690913001816439118925869829536250846639469310212937581855933
518710668619729641309263324784218037304674615635505157625365285797298
443305108038716358762651248086440048468372406494047491988831492829285
161751678332086837187972136968851829414833128243888620308340321378185
123642015152620056914762030047166652837911735649104226834442937368573
819974224203735488718107356908123314371578553175076071717775764345142
549580867720367836084289513946899287311856029114297
4. Literature
[1] D. Elliott, P. Dober “Symmetry in Physics, Vol. 1“, MIR Publishing House, 1983
[2] “Schrödinger equation”, en.wikipedia.org/wiki/Schrodinger equation.
[3] P.S. Alexandrov “Introduction to the theory of groups”, Moscow SCIENCE, GRFML, 1980.
[4] “RSA“, ru.wikipedia.org/wiki/RSA.
[5] “Test Farm“, ru.wikipedia.org/wiki/Test_Farm.
[6] “Euler's function“, http: //ru.wikipedia.org/wiki/Eyler_Function.
[7] “General sieve of numerical field“, en.wikipedia.org/wiki/General_method_reshet_number_field.
[8] “Numbers of Mersenne“, http: //ru.wikipedia.org/wiki/Number of Mersenne.
1. Introduction
In our world, everything is interconnected, it seems to each other, it has the same or similar parameters. Often these properties are called symmetry. In the "Concise Oxford Dictionary", symmetry is defined as "Beauty due to the proportionality of body parts or any whole, balance, similarity, harmony, consistency." [1] Very often, symmetry manifests itself in mathematics and physics. In physics, the properties of symmetry are clearly manifested in quantum mechanics and its mathematical apparatus, for example, the Schrödinger equation [2]. In mathematics there is a special mathematical apparatus, operating with the concepts of similarity and symmetry. This mathematical apparatus is called group theory [3]. One of the practical applications of symmetry in mathematics is RSA public key encryption [4].
2. Matrix of residuals of a prime number
Consider the definition of deduction and comparison by module. Here is the definition given in the modern explanatory dictionary. The number “a“ is called the residue of the number “b“ modulo “m“ if the difference “a - b“ is divided by “m“ (a, b, m> 0 are integers). That is, “a“ is comparable to “b“ modulo “m“.
a ≡ b (mod m)
')
This means that if “a“ is not completely divided by “m”, then “b“ is the remainder of dividing “a“ by “m“. Two integers “a“ and “b“ are comparable modulo a natural number “m“ if they give identical residues when divided by “m“.
Take a simple integer and denote it by “b”. The set of integers in the interval (1,2,3, ... b-1) is denoted by “B“. If this set is written in the form of a column, in ascending order from bottom to top, then we get the matrix column. All numbers in this column are arranged one after another, their number is equal to “b - 1“. Denote this column by the number “1“. Each number from the set “B“ is squared and divided by “b“ with the remainder. The resulting remnants of the remainder will write in the column. Denote this column by the number “2“ and place it to the right of column number “1“. It is necessary to arrange the remains so that they correspond to the numbers squared, and are with them in one straight line. After that, we will raise each number from the set “B“ to the third degree and divide it by “b“ with the remainder. From the obtained residues, we form a column with the number “3“, by analogy with column number “2“. Further, by analogy, we raise to the next degree and find the remains of division by “b“. We perform actions as long as the exponent in which we build numbers from the set “B“ is less than “b“. As a result, we obtain a square matrix of size (b-1) x (b-1).
An example of such a square matrix for a prime integer “b = 23” is shown in Fig.1.

Fig. 1 Matrix of residuals of a simple integer b = 23.
The resulting matrix has amazing properties:
- It is clearly seen that the last column of the matrix consists of one units. This is fully consistent with the Farm simplicity test. A n-1 ≡ 1 (mod N) [5].
- It should be noted that the column with the number (b-1) / 2 (“b“ minus 1 divided by 2) consists of only two values of the set “B“. These are the values 1 and (b-1).
- The values of the numbers, the sets “B“, in the columns are symmetrical about the middle of the interval, i.e. value pairs (b-1) / 2 and (b + 1) / 2.
- The types of symmetry for different columns are different.
- For columns with even numbers, the values are equidistant from the middle of the interval, i.e. the pairs of values (b-1) / 2 and (b + 1) / 2 are the same. For the matrix shown in Fig. 1, the remainder of 11 squared divided by 23 and the remainder of 12 squared divided by 23 are equal and equal to 6.
- For columns with odd numbers, the values equidistant from the middle of the interval, i.e. The value pairs (b-1) / 2 and (b + 1) / 2 are always equal to “b“. For the matrix shown in Fig. 1, the remainder of 11 in the third degree, divided by 23, is 20, the remainder of 12 in the third degree, divided by 23, is 3. In total, these two residues are 23, i.e. are equal to “b“.
All properties described above and considered for the matrix shown in fig. 1, are inherent in matrices constructed according to the same rules for other simple integers.
3. Matrix residual composite number
The matrix considered in Section 2 characterizes the symmetry of primes. For composite numbers, the matrix constructed by the same rules is significantly different. It inherits the properties of the matrix of a prime number, but acquires new properties. Consider a composite number that is a product of two primes “x“ and “y“. Similarly, the value of a number is denoted by “b“, and the set of all numbers in the interval (1, b-1) is denoted by “B“. Consider the composite number “b = 35“, which is the result of multiplying the primes “x = 5“ and “y = 7“. We construct a matrix of residues of various degrees for the numerical interval (35-1). The residual matrix is shown in Fig. 2

Fig. 2 Residual matrix of composite number b = 35.
Some properties are inherited from the matrix of residues of a prime number. For example, the values of the numbers present in the columns are symmetric about the middle of the values of the numerical interval, i.e. values (b-1) / 2 and (b + 1) / 2.
The matrix shown in Fig. 2, bears in itself new properties:
- The values of the rows of the matrix, in which the first column contains multiples of divisors of a composite number, take numerical values of multiples of the divisors of a composite number and are never equal to 1. For example, in the matrix of Fig. 2, row 5, in the second column, has the value 25, in the third 20, in the fourth 30 and so on. All these values are multiples of 5.
- If we exclude rows whose values are multiples of the divisors of the number “b“, then there will necessarily be two columns in which the remaining values are 1. For example, in fig. 2 are columns with numbers 12, 24.
- Of these two selected columns, the largest column number is the product (x-1) by (y-1). Those. if from each of the factors, subtract 1 and multiply them, then we get the number of the largest selected column. For the matrix in fig. 2 factors of the number “b“ are 5 and 7. If we subtract 1 from each of them and multiply, we get (5-1) x (7-1) = 24. This is exactly the number of the largest selected column. It should be noted that in this case, the column number is equal to the Euler function, whose value is (x-1) x (y-1) = (n). [6].
- The second column must contain four values equal to 1. For the matrix of residues of a prime number and the values of the set “B” equal to (1, b-1), the values in the second column take the value 1. For the matrix of residues of a composite number, there are two more numbers the sets “B“, in the case of which they are squared and divided by “b“, the remainder is 1. In Fig. 2 are numbers 6 and 29.
- There are always pairs of numbers, sets “B“, following each other, the values of which are multiples of the divisors “x” and “y” of the number “b”. For the matrix in fig. 2 are pairs (14, 15) and (20, 21).
All properties described above and considered for the matrix shown in fig. 2, are inherent in matrices constructed according to the same rules for other composite integers.
4. Factoring numbers
If we consider the RSA public key encryption method [4], then its use is based on the existence of mutually opposite mappings in the matrix of residuals of a composite number. If we take the composite number “b“, there are always two columns “c“ and “d“ in its residue matrix, for which the following conditions are true:
(b1 ** c) ≡ c1 (mod b); (c1 ** d) ≡ d1 (mod b); b1 = d1
where b1, c1, d1 are numeric values in columns 1, c, d.
That is, for the composite number “b“ there always exist two numbers “c“, “d“ from the range (1, b-1) for which the sequence of actions is valid:
- We define the remainder of any number “b1“ from the range (1, b-1) raised to the power of “c“ and divided by “b“. We denote this remainder by “c1“.
- The resulting residue “c1“ will be raised to the power of “d“ and divided into “b“ with the remainder. We denote this remainder by “d1“.
- The resulting residue “d1“ is always equal to “b1“.
For the RSA encryption algorithm, (c, b) is the public key, (d, b) is the secret key.

Fig. 3 Residual matrix of the composite number b = 33.
Consider the matrix of residuals of the number b = 33, fig. 3. For this number c = 3, d = 7. Take any number from the first column, for example, 8 and raise it to the 3rd power, the remainder is 17. We raise 17 to the power 7, the remainder is 8, i.e. this remainder is equal to the original number from the first column.
RSA is one of the common public key encryption algorithms. Together with the improvement of encryption methods, methods for decrypting secret messages are being improved.
Often, the decryption task for RSA is attempted in the forehead, i.e. find the divisors of the base composite number. These methods are called factorization of numbers. In addition to a simple enumeration of values and verification of numbers, use the quadratic sieve method.
The basis of this method is that part of the residuals from squaring and dividing by the number “b“ are full squares of numbers. In fig. 2 full squares are the quadratic residues of the numbers (11, 12, 17), from the first column. To find the divisors of the number “b“, it is necessary to extract the square root from the quadratic remainder. The result, i.e. square root, subtract from the number “b“ or add to the number “b“. Multiple divisors of the number “b” will be obtained. Using the Euclidean algorithm, one can find the divisors of the number “b“.
In fig. 2, for the number 11, the quadratic remainder is 16. We extract the square root of 16, it is 4. We add 4 to 11, we get 15, a multiple of the divisor 5. We take 4 from 11, we get 7, the number is equal to 7.
One of the most modern methods of factoring numbers is the sieve method of a number field [7]. This method allows reducing the number of values to be checked and reducing the time for performing calculations. The use of the sieve method of the numerical field and the properties of the matrix of residuals of the composite number makes it possible to achieve even more powerful results.
For experimental verification of the methods of factorization of numbers, you can use the so-called Mersenne numbers [8]. These numbers are the number 2 to the power of “n“, minus 1, where the “n“ is a natural number. Only a limited number of Mersenne numbers are simple; the rest are decomposed into a finite number of divisors.
As an illustrative example, one of the divisors, the number 2 to the power of 4099, minus 1, is equal to -
431654595928296534254101974033397155588925169723783332084380283993261
209600632883153055473166663136594966053411838575253500155337120152873
781979635198920643526624304319945635699208877607737201529464080041890
547345467573782661041054825447947267620282789541695832747170633177331
920343746996221855049648583763367504662477325712779883313257418325242
923223374882540094860518718525171060169694349915604794431233943848839
032331927197514745282594881581533286782002526616104836932259305133211
436643050243706215479754994805351437606942854754835739144357537526269
041212016993538655106720507482318994547865735219931202814880677303379
021540170667630675512896640229254326407201860556265718380698467494757
374722667518146123812589844575734597771351069823560862537030159862538
798769879690913001816439118925869829536250846639469310212937581855933
518710668619729641309263324784218037304674615635505157625365285797298
443305108038716358762651248086440048468372406494047491988831492829285
161751678332086837187972136968851829414833128243888620308340321378185
123642015152620056914762030047166652837911735649104226834442937368573
819974224203735488718107356908123314371578553175076071717775764345142
549580867720367836084289513946899287311856029114297
4. Literature
[1] D. Elliott, P. Dober “Symmetry in Physics, Vol. 1“, MIR Publishing House, 1983
[2] “Schrödinger equation”, en.wikipedia.org/wiki/Schrodinger equation.
[3] P.S. Alexandrov “Introduction to the theory of groups”, Moscow SCIENCE, GRFML, 1980.
[4] “RSA“, ru.wikipedia.org/wiki/RSA.
[5] “Test Farm“, ru.wikipedia.org/wiki/Test_Farm.
[6] “Euler's function“, http: //ru.wikipedia.org/wiki/Eyler_Function.
[7] “General sieve of numerical field“, en.wikipedia.org/wiki/General_method_reshet_number_field.
[8] “Numbers of Mersenne“, http: //ru.wikipedia.org/wiki/Number of Mersenne.
Source: https://habr.com/ru/post/218053/
All Articles