State space search

We continue the series of posts about artificial intelligence, written based on the performance in the Technopark Mail.ru Konstantin Anisimovich - director of technology development department ABBYY. The second article will be devoted to search algorithms.


Depending on what kind of knowledge representation we choose - declarative or productional - we determine the way knowledge is applied. With the production system, everything is quite simple: we directly interpret the products.

If we chose a declarative presentation of knowledge, then everything happens a little more complicated. To do this, we need to implement a search in the state space . The fact is that the structured representations of knowledge are organized hierarchically. And if we try to apply a hierarchical description to the input data, then at each of its levels we will get possible options for interpreting the data - hypotheses.
')
In order to effectively choose one or more of the best hypotheses, while avoiding a combinatorial explosion, state space search algorithms are used.

The state space arises when the solution is split into separate steps. Here the initial state is highlighted, when we have not chosen a hypothesis, as well as the final state, when we have found a hypothesis, which is a valid solution to our problem. In the process of searching for this hypothesis there are operations of transition to the next state. It is not difficult to notice that the spatial state has an exponential complexity depending on the numerical steps. If we aim at going around the entire state space, we need exponential time.

To avoid this problem, different search algorithms are used. They are divided into two types - brute force and heuristic search. As is already clear, in the overwhelming majority of cases, complete exhaustion is not suitable (unless we solve a very small task), but it has some educational value. Therefore, we consider it first, and you, if you are well acquainted with it, you can immediately go to the heuristic type .

Search using brute force

There are the following types of exhaustive search : search in width, search in depth and search with iterative deepening.
During the search in width, we take all possible steps in the spatial state of the initial state and obtain a new set of states. Then from each state of this set we again do all possible steps, we obtain the following set of states, and so on - until we find a solution. Graphically, the search in width can be represented as the motion of a front in the state space.

Search in depth means that we take one step from the initial state, then take another step from the new state, etc., until we reach the final state or a state from which no other step can be taken. In this case, we recursively go back and take steps again from the state to which we returned, until we find a solution.
It is easy to see that such a wide search has an exponential complexity both in time and in memory. And the depth search has exponential time complexity. Of course, we can get lucky, and there will be a solution right away, but in practice this is unlikely.

An iterative deepening search is an optimization of the search in depth and in width, which is guaranteed to allow you to find the solution closest to the initial state, avoiding exponential complexity. How is this algorithm implemented? We are looking for depth with depth limiting by constant N. We have found a solution - good. We did not find it - repeat the search in depth with the constant N + 1 and so on until it is found. This algorithm, although simple to implement, is only suitable for the simplest of tasks.

Heuristic search

Most often, practical problems are solved using heuristic search. The heuristic search is based on the state evaluation function. Unlike the full brute force algorithms, heuristic search allows ranking spatial states based on their “perspective”. Heuristic search searches in the state space more purposefully than full brute-force algorithms. It is important that in many problems state assessment is the best estimate of the way to achieve this state from the initial one. If such an estimate is possible in our problem, then the heuristic search algorithms are greatly simplified.

The main class of heuristic search algorithms is a search from the best state. It includes three basic algorithms: these are greedy search, ray search and A *. Their general idea is based on maintaining the set of reached states in the search process and choosing one or several best states at each step.

The simplest of them is the greedy search . If it is applied in the task of finding the best path in a graph, this will give the well-known Dijkstra algorithm . Greedy search, choosing the state from which the search will continue, searches for the state with the best estimate of the path from the initial to the given one. Therefore, it is called "greedy" - because "enough" is the best condition at the moment, not thinking about the consequences. Naturally, like many greedy algorithms, such a strategy does not lead to an optimal solution. End states are often reached in too long, non-optimal ways. In addition, the greedy search must constantly support the sets of all the reached states, which may be too many, which causes excessive memory consumption.

The ray search algorithm and the A * algorithm are attempts to improve the behavior of the greedy search and correct these two inherent problems. Beam search works as follows: at each step we maintain some set of N best states. Next, from each of these states we do all possible steps and get a lot of states of the next generation. In this set we remove duplicates, that is, the same states. We estimate the remaining ones and sort them in order of deterioration. Next, select the N best, and so on until we find the final state of interest.

Radiation search has its advantages and disadvantages. Its main disadvantage is that, unlike the greedy, ray search does not guarantee finding the final state with the best quality, because in the process of moving the front, the best state may fall out of it. In practice, this can be fought by adjusting the width of the front. The front already, the faster the algorithm works, but the more often it is mistaken. The wider the front, the better the algorithm works, but the longer it takes. This is one of its important advantages - the ability to easily balance between speed and quality. Radiation search is very popular in the academic environment, especially among Chinese scientists. It is simple to implement and works quite well.

The idea of ​​the A * algorithm is that at each step we choose not the best, but the most promising state at the moment. The state through which the path to the best final state is most likely to pass.

The heuristic lower estimate of the remainder of the path to the final state is added to the assessment of the current state in algorithm A *. If the heuristic lower estimate is good enough, then A * works efficiently and quickly finds the best state. In this case, A * will be polynomial in the number of steps, and not exponential. A * is a really good algorithm, in my work I use it much more often than ray search.

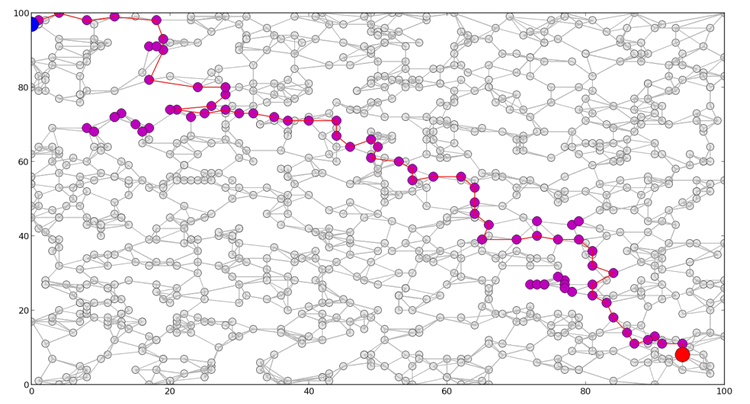
The disadvantage of the A * algorithm is the need to invent heuristics. For the sake of justice, it must be said that in many problems this heuristic is fairly easy and natural. In such tasks, it is recommended to use A *. If heuristics do not work out, then ray search comes to the rescue.

In the third post of this series, we will discuss methods for obtaining knowledge used in the creation of artificial intelligence, as well as machine learning - in particular, those methods used in FineReader.