Mathematics for testers
Nikita Nalyutin's report at the SQA Days conference - 13, April 26-27, 2013, St. Petersburg, Russia
Announcement . New test design techniques were not always born at once, not everything in engineering practice can result from only one insight and brilliant ideas seen in a dream. A sufficiently large part of modern testing practices emerged as a result of the painstaking theoretical and experimental work on the adaptation of mathematical models. And, although in order to be a good tester, it is not at all necessary to be a mathematician, it is useful to understand which theoretical basis underlies this or that testing method. In the report, I will talk about what the basis for testing provides mathematical logic, the theory of formal languages, mathematical statistics and other branches of mathematics; what areas related to testing exist in theoretical computer science; what new methods can be expected in the near future

')
Good afternoon, dear colleagues! My name is Nikita Nalyutin . I hope I can brighten up your afternoon nap with a small talk about math testing. First, I will tell you a little about who I am and how I came to testing.
I came to testing eleven years ago from development. He started as an automator tester, was engaged in testing aviation software. If you fly Airbus airplanes, probably two or three systems on board today passed through my hands. After that, he worked in various subject areas: he was engaged in testing trading systems at Deutsche Bank, and he did a little work in a wonderful Undev company. Now I work in the company Experian, where I am engaged in test management in Russia, the CIS countries and Europe. In addition to testing directly over the past eleven years, many different interesting things have happened. I teach in three domestic universities. Do not ask how I do it - I do not know. In 2007, managed to release a book on verification and testing, with the support of Microsoft. They say that turned out well.

What will be discussed today? Why do we need mathematics in testing. Why can not we test without mathematics. In which cases such an option is possible, and in which not. For a few examples, let's see how mathematics can be applied in practice. How and where to look when we start testing something new.

Let's talk about how and where you can learn mathematics in the application for testing. And let's talk a little about how you can get into science, while continuing to do testing, is it worth doing it in our practical realities, are anyone interested in doing science now.

Why do we even raise the question of the need for mathematics in testing. Yesterday, at one of the reports, I saw a slide that struck me, the meaning of which was as follows. As a disadvantage of one of the systems, it is indicated that in order to use it, the tester must have developed analytical thinking. It always seemed to me that analytical thinking is one of the strengths of a tester and there is nothing to do in this profession without it. Mathematical logic and analytical thinking, in particular, allow us to make testing as sharp as possible, to develop it to such an extent that we can solve any of the most complex tasks.

In fact, since the time of MV Lomonosov in life has not changed as much as it might seem. Mind needs to be brought in order by everyone, and testers in particular. Testers need special tools. Al-Capone used a revolver and a kind word; for testers, I would suggest using math and a kind word. With the help of mathematics and a kind word with the developers, you can do many different interesting things.
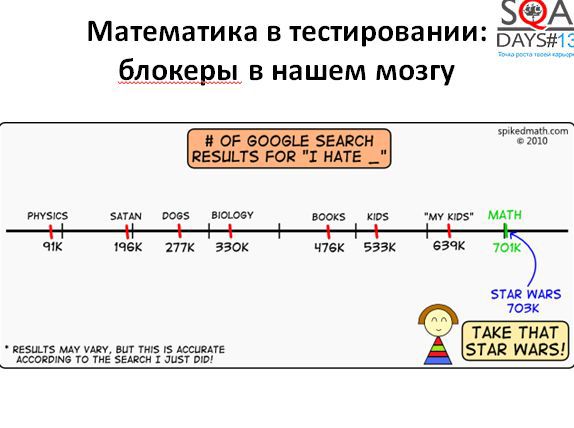
In fact, an interesting question: why do not we use mathematics in our daily activities. The answer is simple - we just do not love her. Simple statistics: take the query in Google, "I hate ...". And we get:
• 703 thousand replies: I hate "Star Wars"
• 701 thousand answers: I hate math
Mathematics is second only to Star Wars! Not bad, right? If this hatred is somewhat decomposed, then three blockers can be distinguished, which do not allow us to use mathematics.

The first blocker - mathematics in testing is a formal proof of the correctness of programs, which does not work well in practice. This area of science is quite well developed and widely known in narrow circles. So extensively that it immediately comes to the mind of many testers, it is worth talking to them about mathematics in testing. The next thought - "this is too high matter, they do not work in practice." So ...
The second blocker - in order for mathematical methods to work, it is necessary to compile detailed specifications. Also far from it. Nobody forces you to write a detailed specification and to prove that the program works correctly. You do not need a detailed mathematical model of the entire system with which you work. You can use mathematics as a small handy tool.
And the most famous blocker, is the thought that
It is not true. I saw with my own eyes an elective on mathematical logic for students of the 5th grade, the guys sat and solved rather complex logical problems. Are you, testers, worse than fifth graders? It seems to me that no.
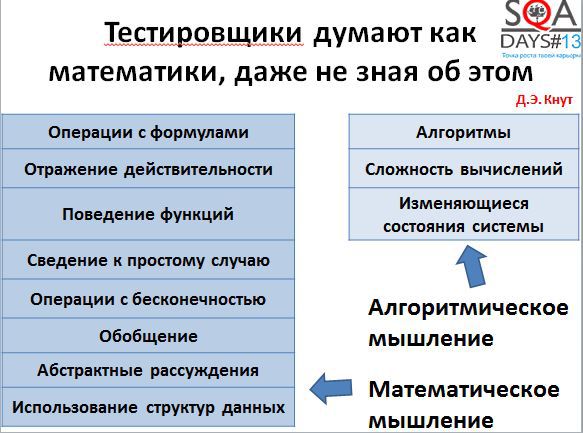
If you try to understand how mathematicians think, the result will be quite interesting. The well-known Donald Knuth wrote an article entitled “Algorithmic Thinking and Mathematical Thinking” (http://www.jstor.org/discover/10.2307/2322871?uid=3738936&uid=2&uid=4&sid=21103388081621). In it, he singled out several types of thinking of mathematicians - algorithmic thinking and mathematical thinking.
All these types of thinking are applicable to testers:
• reflection of reality
In fact, with your tests you reflect reality, showing how well the system works.
• reduction to a simple case
We all try to write tests so that they are as simple as possible and, at the same time, there is no need to over-complicate them.
• generalization
We are trying to describe the tests so that they can be reused. We try to first write a pattern for the test, and then many specific tests on the pattern.
• abstract reasoning
We all build some abstract model of the system in our head, and then we test it.
• changing system state
At a minimum, we have two system states: everything works or everything is broken. Typically, these states are somewhat larger, and during testing we change the state of the system.
If this table did not convince you, you can look at the results of the research by I.Ya. Kaplunovich (Kaplunovich I.Ya. The content of mental operations in the structure of spatial thinking // Questions of psychology. 1987. No. 6), which is engaged in research in the field of psychology of teaching. In his research, he identifies five categories of thinking.

AND I. Kaplunovich believes that from our birth to the moment of mathematical literacy, i.e. There are five stages to the point when our analytical skills are well developed. We start from the topological level, where our disordered thoughts begin to fit into some structure. We move further, at the fourth level we begin to measure, at the fifth level - to optimize.
Doesn't this remind you of anything? That's right - five levels of CMMI: the first level - just gathered, managed. The second and third - we achieve repeatability and controllability, the fourth - we measure, the fifth - we optimize. In fact, it seems.

If we digress from high matters a little, then we can say that all the ideas put forward by mathematicians and good engineers are all, by and large, created by laziness.
We are too lazy to spend a lot of time and solve problems for a long time, so we sit down and come up with something interesting, quickly solve the problem and begin to engage in other tasks. Engineers rarely love the “Long, expensive, boring” approach, mathematics, too. In the test design, laziness works fine - we can be lazy for a long time and with taste, and most importantly - effectively.
Let's try to figure out a few examples of who, how and where can apply mathematics in test design.

Let's start with the most obvious area, with mathematical logic. Since we can use mathematics to optimize the code coverage of our system, while not forgetting that we love being lazy. Here is a small example: the usual “if” with two branches and the long formula in the condition.

My tenth grade geometry teacher called long-long formulas "crocodiles." Here is a crocodile met in our code. In order to cover both branches of the code, you need to understand the structure of the formula, you need to figure out what values the variables x1, x2, x3, x4 take. It is possible, but somehow I really do not want. The question arises: what can we do? It is possible to be lazy unproductive and, having forgotten the mathematics, to test this code with a complete overhaul. Get 16 tests. "Long, expensive, boring." Well, just do not want.
We are trying to reduce the number of tests - we apply MC / DC (11-12 tests), we decide that we have enough coverage on the branches - we get two tests ...
And then - suddenly remember Boolean algebra. After transforming the original expression, we get that only the variable x3 affects the truth value. As a result, we get not only an easy way to generate tests (in one, x3 = true, in the other, x3 = false), but we also get a reason to talk with the developer. After all, it is rather strange when there is a rather complex logical expression in the code, but in fact it depends only on one variable, perhaps there is a mistake somewhere.

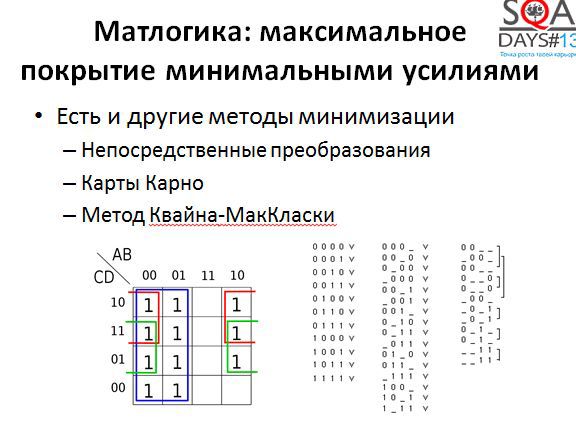
In general, logical expressions can be simplified by other methods. There are at least three methods familiar to all junior technical specialties. Direct transformations using the laws of Boolean algebra always work, Carnot maps are good when there are few variables in the expression, and the Quine-McCluskey method is good even for a large number of variables and is well algorithmic. If you search, you can even find methods for minimizing expressions that take into account the characteristics of the subject area, that is, they are based not only on mathematics.
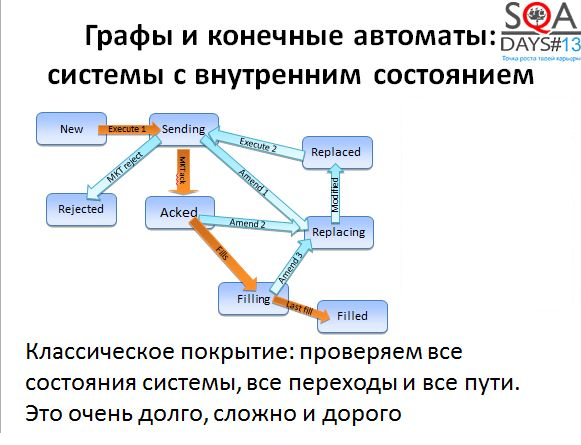
Let's try to make out the next question - the state of the system and the testing of changing states. Usually, there are much more states than just “working” and “not working”, I was a little tricky at the beginning of a speech.

For example, below you can see some of the states that an exchange order passes - an application to buy or sell shares. In order for the transaction to take place, the application must pass through several states. First, the order is created, then it is confirmed by the exchange, then many small deals are made for the purchase and in the end, the required number of shares is bought or sold. All conditions of the exchange order are reflected in the trading systems, all transitions and states must be checked. In fact, everything is somewhat more complicated, but now it does not matter.
Usually, all states, or all transitions, or both are checked. Full coverage is achievable, but traditionally - "Long, expensive, boring." Let's try to make your life easier and be a bit lazy. How?
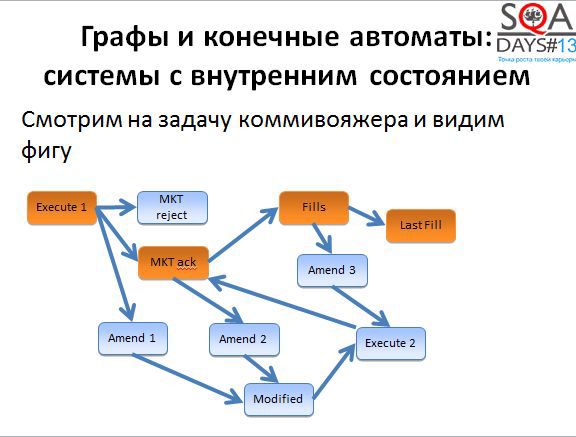
You must have heard about the traveling salesman problem - the optimization problem on graphs. There is a de Broyen algorithm associated with this task.

We do not need to use the algorithm literally, it is enough to understand that it allows us to obtain the optimal or sufficiently optimal set of short paths that we can go through in the graph in order to cover it completely. In order for the algorithm to start working, we need a little work. First, we take the initial states and build a graph in which the vertices correspond to transitions of the original graph. And then we begin to cover the vertices of the new graph (ie, the transitions of the old).
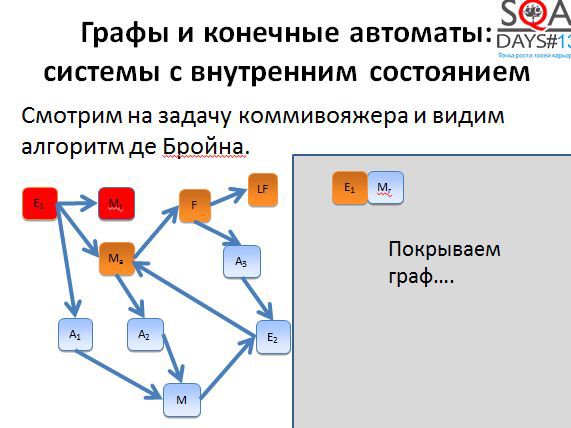
The first two paths are quite short. We begin to build the third way and get very, very long.
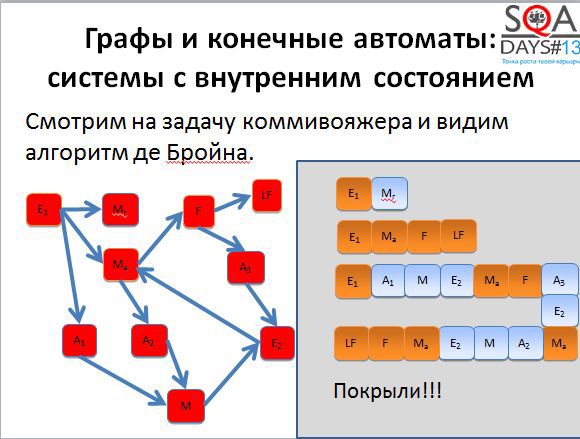

Now imagine such a situation. You have three testers. The first performs the first test, the second - the second test, the third - the third test. The first two complete the work very quickly, but the last one sits for a very long time. And if it is autotests? The third test works for a very long time, the results are obtained with a long delay.
If we apply the de Broyen algorithm, it is possible to cut the third sequence into several shorter ones and parallelize the execution well. We get five tests instead of three, but if they are executed in parallel, testing completes much faster.
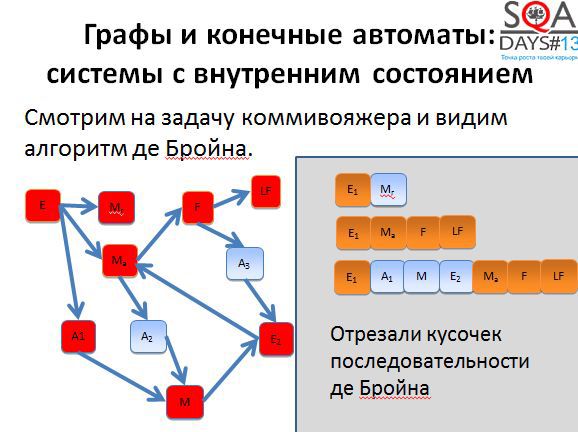
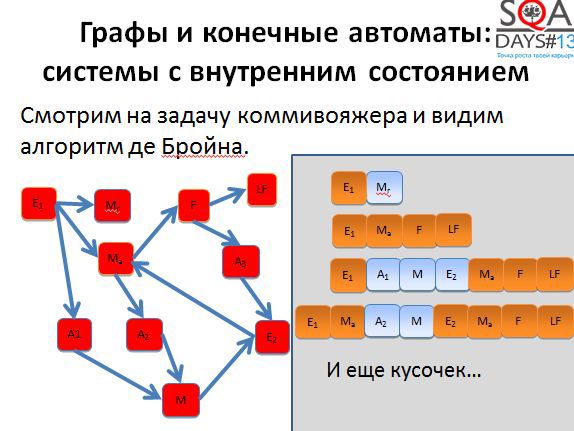
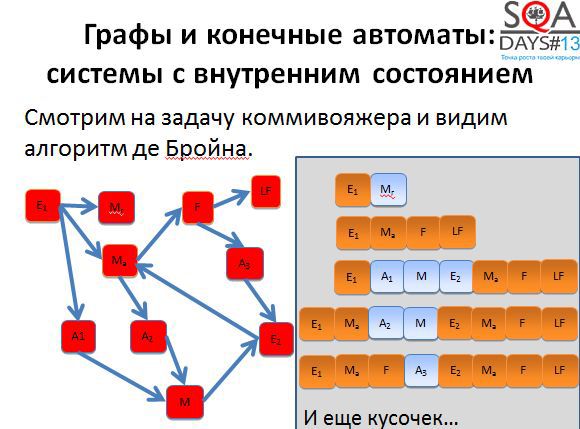

In addition, as more tests appear, more flexibility appears. We can perform all the tests, but we can throw out the little interesting ones, we can place higher priorities on those tests that pass through the most interesting states for us. There are quite a few ways to use the results of the algorithm. And pay attention that the algorithm does not use things specific for the subject area, it works with purely abstract states and transitions. And if you try to come up with your own algorithm, but with the subject area and muses?

The third example. There is a basic concept in testing - the equivalence class. It would seem that you can come up with a new one?

In which equivalence class must be at least one test. Plus you need to check the boundaries of classes. All this works well if you know equivalence classes and know boundary values. Or it may happen that the classes are clearly not set and the boundaries are blurred. It may, for example, be such that equivalence classes are formed due to the operation of the system on certain specific equipment and are not defined in any way in the software requirements.

It is a real example. There is a system that stores in the database rows from 0 to 5 MB in length. The requirements state that the time to save this line should be approximately the same. The classic approach to testing gives us three tests: an empty line, a 5 MB line and an average 2.5 MB line. Checked, the conservation time is the same and fits into the permissible error. All is well.

Put into operation, began to collect real data and found that short strings are stored much faster than long ones. We start experimenting, knowing nothing about the reasons for this behavior, as a result we get the following picture.

It turns out that in addition to these critical points, there are two more: 256 B and 32 KB. Why? We talked with the developer, and received in response a story about what a cool optimization the developer did: strings up to 256 bytes are stored as strings, up to 32K as binary objects in the database, and over 32k - as files on the file system. "All the same, you have few such lines, but the base is easier." Such equivalence classes are much harder to find and analysis of results from the industrial environment or from the acceptance testing environment can come to our aid. If we correctly approach the analysis of these data, then we will be able to find anomalous zones.

If we apply the theory of measurements, we can make the search for anomalous zones more ordered. To obtain a basic representation, you can use at least the definitions from GOST R 50779. The terms defined in this GOST can be used as starting points for further searches in specialized literature and extract exactly the knowledge you need from measurement theory.
Let's try to get useful information about anomalies in our case. There is an interval with known boundary values (minimum, maximum, middle). There is some inaccurate information about what we may consider an anomalous zone. We build the distribution function of the probability that this value will cause problems — for example, that a string of a specified length will be kept for a long time. For example, take the normal distribution. A narrow and sharp dome means high confidence that this zone is abnormal, a wide dome means low confidence, for example, due to the fact that we have little data on these values. Next, we begin to apply selective testing and generate rows of different lengths, “targeting”. Where the dome is narrower, we “shoot” tests more closely, where the wider one is wider, trying to find a more precise pattern.
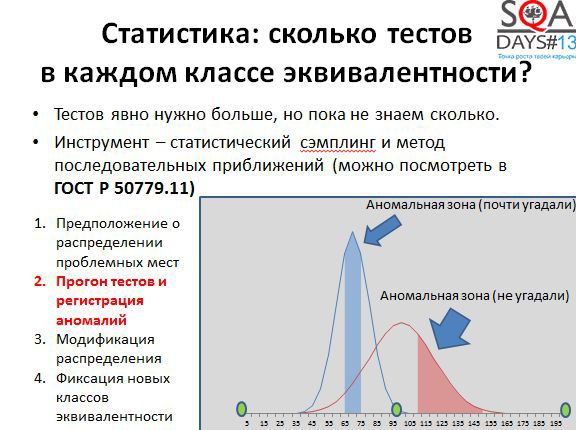
In the screenshot above, you can see: in blue - we guessed the anomalous zone, the lines are saved slowly there, in red - we didn’t guess a little bit - there are no anomalous values of the string saving time to the left of the red zone. Next, we modify the right distribution and “target” again.

The second adjustment showed that we found the anomalous zone more accurately. And we can add six more to our original three boundary values - for each of the two anomalous regions.

Thus, we obtained new equivalence classes that were not visible in advance, but which were derived from the experiment, and which can be used to test the behavior of new versions of the system. .

One more example. , pair-waise . , , , , ( ), , – , .

. …
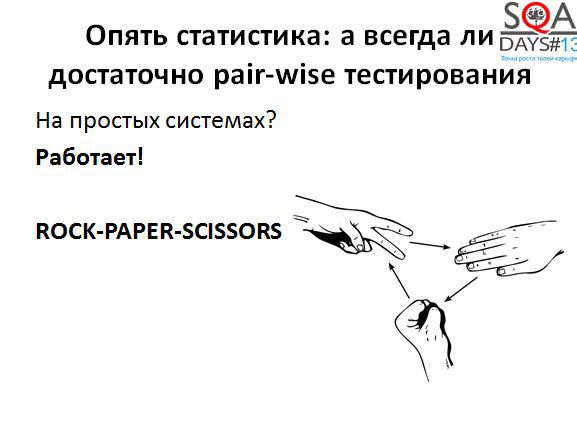
….

, « ».
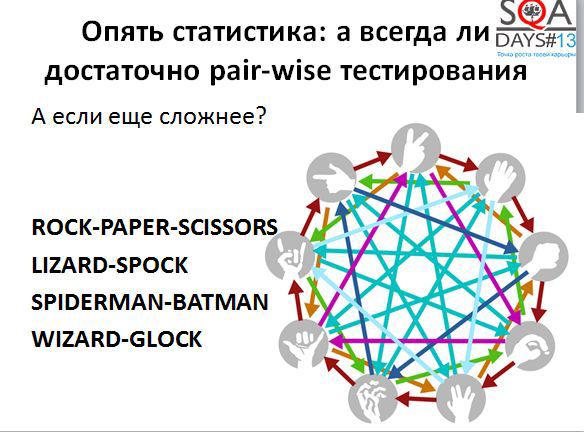
pair-wise ? (NIST).

NIST ACTS, . , pair-wise 65-97% . , , .. k-way , , .

, pair-wise , .
, NIST ACTS.

pair-wise – , n- (, , , …) .

NIST (http://math.nist.gov/coveringarrays/coveringarray.html). , , « ». , -, . NIST ACTS . , .

pair-wise k-way, .
, , . .

, . , -. .

- . IT-, .
-- , , .
, .

, , . – , - . , , . – – .

Software Engineering – . , . – ACM, Association for Computing Machinery. Computer Science Software Engineering, , IT, – IT-.
, ACM .. Curricula – , , IT-, . , , IT-. , . , , – , – . ( ) .

, , – IEEE – Institute of Electrical and Electronics Engineers. (Body of Knowledge), Software Engineering Body of Knowledge, . .

. . , Quality Assurance Institute – , ISTQB. ( ) . , ICST . www.arxiv.org – , . scholar.google.com - . , .

( ) , , .

«?”. , , .
, , , . . . – , . – . , , 2012 , .


– , «?», .
– ( -, , ).
– ( – ).
– , .

, , .
, , .

, , .

, .
Question.
: . , , . , . , . , ?
.
, . , , . . , , – . – , – , , . , «» «» - . , , – .
Question.
, ?
.
, , .
Question.
- , , ?
.
, . , , , , . .
Question.
. , , , ?
.
, . , , . , . , , , . ( ) , .
Question.
, , ? ?
.
. , . , , , , - . , , , .
Announcement . New test design techniques were not always born at once, not everything in engineering practice can result from only one insight and brilliant ideas seen in a dream. A sufficiently large part of modern testing practices emerged as a result of the painstaking theoretical and experimental work on the adaptation of mathematical models. And, although in order to be a good tester, it is not at all necessary to be a mathematician, it is useful to understand which theoretical basis underlies this or that testing method. In the report, I will talk about what the basis for testing provides mathematical logic, the theory of formal languages, mathematical statistics and other branches of mathematics; what areas related to testing exist in theoretical computer science; what new methods can be expected in the near future

')
Good afternoon, dear colleagues! My name is Nikita Nalyutin . I hope I can brighten up your afternoon nap with a small talk about math testing. First, I will tell you a little about who I am and how I came to testing.
I came to testing eleven years ago from development. He started as an automator tester, was engaged in testing aviation software. If you fly Airbus airplanes, probably two or three systems on board today passed through my hands. After that, he worked in various subject areas: he was engaged in testing trading systems at Deutsche Bank, and he did a little work in a wonderful Undev company. Now I work in the company Experian, where I am engaged in test management in Russia, the CIS countries and Europe. In addition to testing directly over the past eleven years, many different interesting things have happened. I teach in three domestic universities. Do not ask how I do it - I do not know. In 2007, managed to release a book on verification and testing, with the support of Microsoft. They say that turned out well.

What will be discussed today? Why do we need mathematics in testing. Why can not we test without mathematics. In which cases such an option is possible, and in which not. For a few examples, let's see how mathematics can be applied in practice. How and where to look when we start testing something new.

Let's talk about how and where you can learn mathematics in the application for testing. And let's talk a little about how you can get into science, while continuing to do testing, is it worth doing it in our practical realities, are anyone interested in doing science now.

Why do we even raise the question of the need for mathematics in testing. Yesterday, at one of the reports, I saw a slide that struck me, the meaning of which was as follows. As a disadvantage of one of the systems, it is indicated that in order to use it, the tester must have developed analytical thinking. It always seemed to me that analytical thinking is one of the strengths of a tester and there is nothing to do in this profession without it. Mathematical logic and analytical thinking, in particular, allow us to make testing as sharp as possible, to develop it to such an extent that we can solve any of the most complex tasks.

In fact, since the time of MV Lomonosov in life has not changed as much as it might seem. Mind needs to be brought in order by everyone, and testers in particular. Testers need special tools. Al-Capone used a revolver and a kind word; for testers, I would suggest using math and a kind word. With the help of mathematics and a kind word with the developers, you can do many different interesting things.

In fact, an interesting question: why do not we use mathematics in our daily activities. The answer is simple - we just do not love her. Simple statistics: take the query in Google, "I hate ...". And we get:
• 703 thousand replies: I hate "Star Wars"
• 701 thousand answers: I hate math
Mathematics is second only to Star Wars! Not bad, right? If this hatred is somewhat decomposed, then three blockers can be distinguished, which do not allow us to use mathematics.

The first blocker - mathematics in testing is a formal proof of the correctness of programs, which does not work well in practice. This area of science is quite well developed and widely known in narrow circles. So extensively that it immediately comes to the mind of many testers, it is worth talking to them about mathematics in testing. The next thought - "this is too high matter, they do not work in practice." So ...
Mathematics is not only a formal verification. We can test using mathematical methods, not proving anything, but simply use mathematics as a tool.
The second blocker - in order for mathematical methods to work, it is necessary to compile detailed specifications. Also far from it. Nobody forces you to write a detailed specification and to prove that the program works correctly. You do not need a detailed mathematical model of the entire system with which you work. You can use mathematics as a small handy tool.
Enough ideas in the head and a small ordering of these ideas, i.e. analytical skills.
And the most famous blocker, is the thought that
math is something very complicated
It is not true. I saw with my own eyes an elective on mathematical logic for students of the 5th grade, the guys sat and solved rather complex logical problems. Are you, testers, worse than fifth graders? It seems to me that no.

If you try to understand how mathematicians think, the result will be quite interesting. The well-known Donald Knuth wrote an article entitled “Algorithmic Thinking and Mathematical Thinking” (http://www.jstor.org/discover/10.2307/2322871?uid=3738936&uid=2&uid=4&sid=21103388081621). In it, he singled out several types of thinking of mathematicians - algorithmic thinking and mathematical thinking.
All these types of thinking are applicable to testers:
• reflection of reality
In fact, with your tests you reflect reality, showing how well the system works.
• reduction to a simple case
We all try to write tests so that they are as simple as possible and, at the same time, there is no need to over-complicate them.
• generalization
We are trying to describe the tests so that they can be reused. We try to first write a pattern for the test, and then many specific tests on the pattern.
• abstract reasoning
We all build some abstract model of the system in our head, and then we test it.
• changing system state
At a minimum, we have two system states: everything works or everything is broken. Typically, these states are somewhat larger, and during testing we change the state of the system.
If this table did not convince you, you can look at the results of the research by I.Ya. Kaplunovich (Kaplunovich I.Ya. The content of mental operations in the structure of spatial thinking // Questions of psychology. 1987. No. 6), which is engaged in research in the field of psychology of teaching. In his research, he identifies five categories of thinking.

AND I. Kaplunovich believes that from our birth to the moment of mathematical literacy, i.e. There are five stages to the point when our analytical skills are well developed. We start from the topological level, where our disordered thoughts begin to fit into some structure. We move further, at the fourth level we begin to measure, at the fifth level - to optimize.
Doesn't this remind you of anything? That's right - five levels of CMMI: the first level - just gathered, managed. The second and third - we achieve repeatability and controllability, the fourth - we measure, the fifth - we optimize. In fact, it seems.

If we digress from high matters a little, then we can say that all the ideas put forward by mathematicians and good engineers are all, by and large, created by laziness.
We are too lazy to spend a lot of time and solve problems for a long time, so we sit down and come up with something interesting, quickly solve the problem and begin to engage in other tasks. Engineers rarely love the “Long, expensive, boring” approach, mathematics, too. In the test design, laziness works fine - we can be lazy for a long time and with taste, and most importantly - effectively.
Let's try to figure out a few examples of who, how and where can apply mathematics in test design.

Let's start with the most obvious area, with mathematical logic. Since we can use mathematics to optimize the code coverage of our system, while not forgetting that we love being lazy. Here is a small example: the usual “if” with two branches and the long formula in the condition.

My tenth grade geometry teacher called long-long formulas "crocodiles." Here is a crocodile met in our code. In order to cover both branches of the code, you need to understand the structure of the formula, you need to figure out what values the variables x1, x2, x3, x4 take. It is possible, but somehow I really do not want. The question arises: what can we do? It is possible to be lazy unproductive and, having forgotten the mathematics, to test this code with a complete overhaul. Get 16 tests. "Long, expensive, boring." Well, just do not want.
We are trying to reduce the number of tests - we apply MC / DC (11-12 tests), we decide that we have enough coverage on the branches - we get two tests ...
And then - suddenly remember Boolean algebra. After transforming the original expression, we get that only the variable x3 affects the truth value. As a result, we get not only an easy way to generate tests (in one, x3 = true, in the other, x3 = false), but we also get a reason to talk with the developer. After all, it is rather strange when there is a rather complex logical expression in the code, but in fact it depends only on one variable, perhaps there is a mistake somewhere.

In general, logical expressions can be simplified by other methods. There are at least three methods familiar to all junior technical specialties. Direct transformations using the laws of Boolean algebra always work, Carnot maps are good when there are few variables in the expression, and the Quine-McCluskey method is good even for a large number of variables and is well algorithmic. If you search, you can even find methods for minimizing expressions that take into account the characteristics of the subject area, that is, they are based not only on mathematics.

Let's try to make out the next question - the state of the system and the testing of changing states. Usually, there are much more states than just “working” and “not working”, I was a little tricky at the beginning of a speech.

For example, below you can see some of the states that an exchange order passes - an application to buy or sell shares. In order for the transaction to take place, the application must pass through several states. First, the order is created, then it is confirmed by the exchange, then many small deals are made for the purchase and in the end, the required number of shares is bought or sold. All conditions of the exchange order are reflected in the trading systems, all transitions and states must be checked. In fact, everything is somewhat more complicated, but now it does not matter.
Usually, all states, or all transitions, or both are checked. Full coverage is achievable, but traditionally - "Long, expensive, boring." Let's try to make your life easier and be a bit lazy. How?


You must have heard about the traveling salesman problem - the optimization problem on graphs. There is a de Broyen algorithm associated with this task.

We do not need to use the algorithm literally, it is enough to understand that it allows us to obtain the optimal or sufficiently optimal set of short paths that we can go through in the graph in order to cover it completely. In order for the algorithm to start working, we need a little work. First, we take the initial states and build a graph in which the vertices correspond to transitions of the original graph. And then we begin to cover the vertices of the new graph (ie, the transitions of the old).

The first two paths are quite short. We begin to build the third way and get very, very long.


Now imagine such a situation. You have three testers. The first performs the first test, the second - the second test, the third - the third test. The first two complete the work very quickly, but the last one sits for a very long time. And if it is autotests? The third test works for a very long time, the results are obtained with a long delay.
If we apply the de Broyen algorithm, it is possible to cut the third sequence into several shorter ones and parallelize the execution well. We get five tests instead of three, but if they are executed in parallel, testing completes much faster.




In addition, as more tests appear, more flexibility appears. We can perform all the tests, but we can throw out the little interesting ones, we can place higher priorities on those tests that pass through the most interesting states for us. There are quite a few ways to use the results of the algorithm. And pay attention that the algorithm does not use things specific for the subject area, it works with purely abstract states and transitions. And if you try to come up with your own algorithm, but with the subject area and muses?

The third example. There is a basic concept in testing - the equivalence class. It would seem that you can come up with a new one?

In which equivalence class must be at least one test. Plus you need to check the boundaries of classes. All this works well if you know equivalence classes and know boundary values. Or it may happen that the classes are clearly not set and the boundaries are blurred. It may, for example, be such that equivalence classes are formed due to the operation of the system on certain specific equipment and are not defined in any way in the software requirements.

It is a real example. There is a system that stores in the database rows from 0 to 5 MB in length. The requirements state that the time to save this line should be approximately the same. The classic approach to testing gives us three tests: an empty line, a 5 MB line and an average 2.5 MB line. Checked, the conservation time is the same and fits into the permissible error. All is well.

Put into operation, began to collect real data and found that short strings are stored much faster than long ones. We start experimenting, knowing nothing about the reasons for this behavior, as a result we get the following picture.

It turns out that in addition to these critical points, there are two more: 256 B and 32 KB. Why? We talked with the developer, and received in response a story about what a cool optimization the developer did: strings up to 256 bytes are stored as strings, up to 32K as binary objects in the database, and over 32k - as files on the file system. "All the same, you have few such lines, but the base is easier." Such equivalence classes are much harder to find and analysis of results from the industrial environment or from the acceptance testing environment can come to our aid. If we correctly approach the analysis of these data, then we will be able to find anomalous zones.

If we apply the theory of measurements, we can make the search for anomalous zones more ordered. To obtain a basic representation, you can use at least the definitions from GOST R 50779. The terms defined in this GOST can be used as starting points for further searches in specialized literature and extract exactly the knowledge you need from measurement theory.
Let's try to get useful information about anomalies in our case. There is an interval with known boundary values (minimum, maximum, middle). There is some inaccurate information about what we may consider an anomalous zone. We build the distribution function of the probability that this value will cause problems — for example, that a string of a specified length will be kept for a long time. For example, take the normal distribution. A narrow and sharp dome means high confidence that this zone is abnormal, a wide dome means low confidence, for example, due to the fact that we have little data on these values. Next, we begin to apply selective testing and generate rows of different lengths, “targeting”. Where the dome is narrower, we “shoot” tests more closely, where the wider one is wider, trying to find a more precise pattern.

In the screenshot above, you can see: in blue - we guessed the anomalous zone, the lines are saved slowly there, in red - we didn’t guess a little bit - there are no anomalous values of the string saving time to the left of the red zone. Next, we modify the right distribution and “target” again.

The second adjustment showed that we found the anomalous zone more accurately. And we can add six more to our original three boundary values - for each of the two anomalous regions.

Thus, we obtained new equivalence classes that were not visible in advance, but which were derived from the experiment, and which can be used to test the behavior of new versions of the system. .

One more example. , pair-waise . , , , , ( ), , – , .

. …

….

, « ».

pair-wise ? (NIST).

NIST ACTS, . , pair-wise 65-97% . , , .. k-way , , .

, pair-wise , .
, NIST ACTS.

pair-wise – , n- (, , , …) .

NIST (http://math.nist.gov/coveringarrays/coveringarray.html). , , « ». , -, . NIST ACTS . , .

pair-wise k-way, .
, , . .

, . , -. .

- . IT-, .

-- , , .
, .

, , . – , - . , , . – – .

Software Engineering – . , . – ACM, Association for Computing Machinery. Computer Science Software Engineering, , IT, – IT-.
, ACM .. Curricula – , , IT-, . , , IT-. , . , , – , – . ( ) .

, , – IEEE – Institute of Electrical and Electronics Engineers. (Body of Knowledge), Software Engineering Body of Knowledge, . .

. . , Quality Assurance Institute – , ISTQB. ( ) . , ICST . www.arxiv.org – , . scholar.google.com - . , .

( ) , , .

«?”. , , .
, , , . . . – , . – . , , 2012 , .


– , «?», .
– ( -, , ).
– ( – ).
– , .

, , .
, , .

, , .

, .
Question.
: . , , . , . , . , ?
.
, . , , . . , , – . – , – , , . , «» «» - . , , – .
Question.
, ?
.
, , .
Question.
- , , ?
.
, . , , , , . .
Question.
. , , , ?
.
, . , , . , . , , , . ( ) , .
Question.
, , ? ?
.
. , . , , , , - . , , , .
Source: https://habr.com/ru/post/217743/
All Articles