How I tried to crack Bitcoin
Recently there was an article in which it was told about an attempt to outwit Bitcoin using a neural network. I went the other way, and I didn’t work out of this practically useful result, but despite this, I don’t consider my experience a complete failure. Firstly, I don’t think because it’s foolish to hope to just take and crack Bitcoin, and secondly, because the expected result was obtained, which means we can say that I did achieve some success. And so, I decided to share the developments with the readers of Habr.
It is believed that some functions in the opposite direction do not work. Wikipedia in the article operates with such a thing as “computational impossibility”. In one of the kamentov , the function was given as an example.
X = A MOD B
Someone may say that this function is in the opposite direction unsolvable. I believe that this function is very solvable, just in the opposite direction it gives an infinite number of pairs (A, B), if we know “B”, then the solution will be an infinite number of possible numbers “A”. Not exactly what we would like, but we didn’t think we were in a fairy tale? This is somewhat similar to pulling out one equation from the system of equations - each equation in the system gives a set, but in the system the intersection of these sets gives a small number of solutions. Therefore, just as we do not separately solve each equation in the system of equations, it makes no sense to consider such functions in isolation from other functions that the cryptoalgorithm consists of. Therefore, the elementary operations of the cryptoalgorithm cannot be viewed separately, and if you look at them as a system of equations, you can theoretically solve it. And it turns out that, by analogy, you can count sha256 in the opposite direction; you just need to transfer the same idea of working with lists to bitwise operations. But we will begin, of course, not with sha-256, but with trivial examples.
')
Suppose we have bit variables a, b, c. Suppose we also know that as a result of taking a & b, we got 0, and the “c” bit did not participate in the formula. Let's try to "lose" this formula in the opposite direction. We know that the AND operation gives us a total of zero if at least one of the operands arriving at its input is zero. Thus, the possible values of abc, as they are seen by the operand “a”, can be represented by a list of one regesp 0 **. Where the asterisk means 0 or 1. Possible values of the abc variables, as they appear to the operand “b” can be represented by a list from the regexp * 0 *. We need the list because in large expressions of one regexp is not enough for us. By regexp, I mean not a traditional regular expression, but a stripped-down version of it, in which an asterisk means any value of the corresponding bit.
When we take a logical "And" over the lists coming to the inputs, we need to combine each incoming regexp to the right input with each incoming to the left. In this task, it is simple for us - it enters only one regexp, so we combine them. For "And", if you need to get 0 at the output - the left list is simply supplemented with the right one. Schematically, I showed it in the picture in the form of a graph:

Explanation. The result f is fed from below, to the exit, and rises in the direction opposite to the arrows - up, splitting at the nodes, until it comes to the final variable. The final variable forms the list of possible values of the variables (the one seen from the position of this variable) necessary to achieve the result. For the variable "a" it is 0 **, for the variable "b" it is * 0 *. In fact, these are all asterisks, but only one of them, in the variable position, is replaced by the incoming f. Further, this list goes down the arrows, combining in nodes with other similar lists. I added the variable "c" specifically to show that the variables not participating in the expression do not interfere with us, but go down in the original form. At the exit, we received a list of two regexps. Each regexp defines a set of possible values that, if desired, we can easily generate from this regexp. This is the answer.
Of course, if there are many elements in the list, we must somehow combine non-contradictory regexps and exclude duplicates, this moment is important, but optimizing, and therefore it is now irrelevant for understanding the idea. About him will be lower.
Now the same, but only for f = 1. We get a = 1 **, b = * 1 *. The rule of combining, if for “I” we need to get 1 at the output - it is more difficult We must combine with the right and left side consistent regexps, while building a list of new regexps. I got the following final rules:
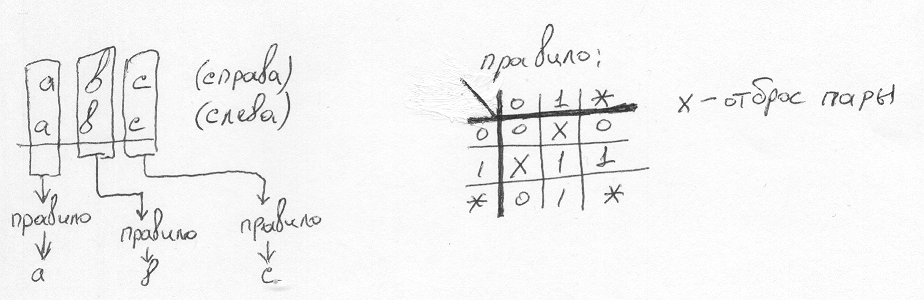
Regexps are viewed bit by bit. Depending on the values of the bits on the right and on the left, choose the most specific value, or discard this pair of regexp, if we meet bits that contradict each other.
Having processed the entries according to this rule, we get:

I think the idea is clear. For "OR" and "NOT" you can build similar rules:

It also shows that for the "NOT" log, we operate not with lists of regexps, but from f itself, inverting it. Lists of regexp through "NOT" pass without changes and without inversions.
Thus, for sha256, we can construct a graph, break our message digest into bits, submit these bits to the outputs, and we will return a list of possible values of the variables of the pre-image.
There were no goals to optimize the algorithm as much as possible. It is clear that working with bits through characters is wasteful, and you can greatly increase the speed of the algorithm if you shift it to C and assembler with bitwise operations. However, there is one more way of optimization - minimization of the sizes of lists with which we operate. When combining lists, duplicates and non-contradictory regexes often arise that need to be thrown back. In addition, sometimes, two regexps can be combined into one new one, which in turn can be further optimized. For example, 000100 and 001100 can be combined into 00 * 100, the rule of such a union is relatively easy to output - only changing one bit is permissible, it is only important that the newly created reexpx does not represent any unnecessary values of variables. Therefore, * 0 cannot be combined with 0 *, while receiving **, because ** represents 11, which neither the first nor the second regexp allowed.
In addition, in the lists we will cache lists - we count them once for each f that came from below.
I made the following assumptions
- the original message is shorter than 56 bytes (for Bitcoin it could be assumed that this is the case, in fact, it is not difficult to refuse this simplification);
- we know all the original message, except the first 8 bits.
Of course, this is not a fountain, I understand that 8 unknown bits are small enough to pick them up by brute force, but the goal of the experiment was to test the method. I got this way to find the letter T, knowing sha-256 from the phrase “The quick brown fox jumps over the lazy dog”, and knowing all the letters of this phrase, except the letter T. The program should work for large unknowns, it will just work longer and will require more memory. For this reason, it is impossible to consider all letters as unknown - there is not enough computing resources, which means there is no practical application. Calculation of the letter T takes 82 seconds per 3GHz Phenom. Of course, a direct enumeration of all unknown bits (256 values) would take a split second, so in this sense there is also no practical use for the program.
It seems to me that there is a possible way of optimization, which is to invent a compact record of sets, but still the method will not work faster than brute force.
Link to a project that finds the letter T: https://github.com/chabapok/sha256unroll
Idea
It is believed that some functions in the opposite direction do not work. Wikipedia in the article operates with such a thing as “computational impossibility”. In one of the kamentov , the function was given as an example.
X = A MOD B
Someone may say that this function is in the opposite direction unsolvable. I believe that this function is very solvable, just in the opposite direction it gives an infinite number of pairs (A, B), if we know “B”, then the solution will be an infinite number of possible numbers “A”. Not exactly what we would like, but we didn’t think we were in a fairy tale? This is somewhat similar to pulling out one equation from the system of equations - each equation in the system gives a set, but in the system the intersection of these sets gives a small number of solutions. Therefore, just as we do not separately solve each equation in the system of equations, it makes no sense to consider such functions in isolation from other functions that the cryptoalgorithm consists of. Therefore, the elementary operations of the cryptoalgorithm cannot be viewed separately, and if you look at them as a system of equations, you can theoretically solve it. And it turns out that, by analogy, you can count sha256 in the opposite direction; you just need to transfer the same idea of working with lists to bitwise operations. But we will begin, of course, not with sha-256, but with trivial examples.
')
Suppose we have bit variables a, b, c. Suppose we also know that as a result of taking a & b, we got 0, and the “c” bit did not participate in the formula. Let's try to "lose" this formula in the opposite direction. We know that the AND operation gives us a total of zero if at least one of the operands arriving at its input is zero. Thus, the possible values of abc, as they are seen by the operand “a”, can be represented by a list of one regesp 0 **. Where the asterisk means 0 or 1. Possible values of the abc variables, as they appear to the operand “b” can be represented by a list from the regexp * 0 *. We need the list because in large expressions of one regexp is not enough for us. By regexp, I mean not a traditional regular expression, but a stripped-down version of it, in which an asterisk means any value of the corresponding bit.
When we take a logical "And" over the lists coming to the inputs, we need to combine each incoming regexp to the right input with each incoming to the left. In this task, it is simple for us - it enters only one regexp, so we combine them. For "And", if you need to get 0 at the output - the left list is simply supplemented with the right one. Schematically, I showed it in the picture in the form of a graph:

Explanation. The result f is fed from below, to the exit, and rises in the direction opposite to the arrows - up, splitting at the nodes, until it comes to the final variable. The final variable forms the list of possible values of the variables (the one seen from the position of this variable) necessary to achieve the result. For the variable "a" it is 0 **, for the variable "b" it is * 0 *. In fact, these are all asterisks, but only one of them, in the variable position, is replaced by the incoming f. Further, this list goes down the arrows, combining in nodes with other similar lists. I added the variable "c" specifically to show that the variables not participating in the expression do not interfere with us, but go down in the original form. At the exit, we received a list of two regexps. Each regexp defines a set of possible values that, if desired, we can easily generate from this regexp. This is the answer.
Of course, if there are many elements in the list, we must somehow combine non-contradictory regexps and exclude duplicates, this moment is important, but optimizing, and therefore it is now irrelevant for understanding the idea. About him will be lower.
Now the same, but only for f = 1. We get a = 1 **, b = * 1 *. The rule of combining, if for “I” we need to get 1 at the output - it is more difficult We must combine with the right and left side consistent regexps, while building a list of new regexps. I got the following final rules:
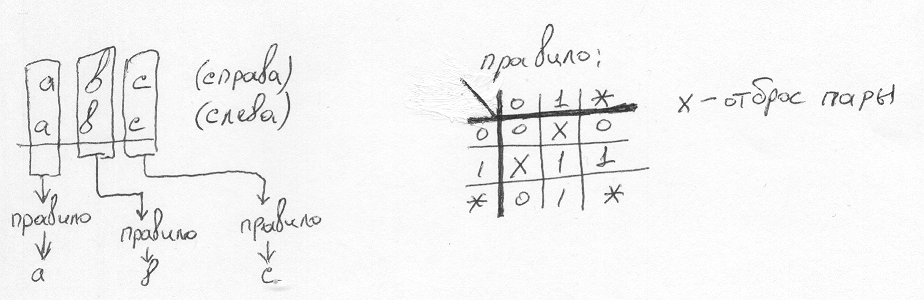
Regexps are viewed bit by bit. Depending on the values of the bits on the right and on the left, choose the most specific value, or discard this pair of regexp, if we meet bits that contradict each other.
Having processed the entries according to this rule, we get:

I think the idea is clear. For "OR" and "NOT" you can build similar rules:

It also shows that for the "NOT" log, we operate not with lists of regexps, but from f itself, inverting it. Lists of regexp through "NOT" pass without changes and without inversions.
Thus, for sha256, we can construct a graph, break our message digest into bits, submit these bits to the outputs, and we will return a list of possible values of the variables of the pre-image.
Optimization
There were no goals to optimize the algorithm as much as possible. It is clear that working with bits through characters is wasteful, and you can greatly increase the speed of the algorithm if you shift it to C and assembler with bitwise operations. However, there is one more way of optimization - minimization of the sizes of lists with which we operate. When combining lists, duplicates and non-contradictory regexes often arise that need to be thrown back. In addition, sometimes, two regexps can be combined into one new one, which in turn can be further optimized. For example, 000100 and 001100 can be combined into 00 * 100, the rule of such a union is relatively easy to output - only changing one bit is permissible, it is only important that the newly created reexpx does not represent any unnecessary values of variables. Therefore, * 0 cannot be combined with 0 *, while receiving **, because ** represents 11, which neither the first nor the second regexp allowed.
In addition, in the lists we will cache lists - we count them once for each f that came from below.
Experiment
I made the following assumptions
- the original message is shorter than 56 bytes (for Bitcoin it could be assumed that this is the case, in fact, it is not difficult to refuse this simplification);
- we know all the original message, except the first 8 bits.
Of course, this is not a fountain, I understand that 8 unknown bits are small enough to pick them up by brute force, but the goal of the experiment was to test the method. I got this way to find the letter T, knowing sha-256 from the phrase “The quick brown fox jumps over the lazy dog”, and knowing all the letters of this phrase, except the letter T. The program should work for large unknowns, it will just work longer and will require more memory. For this reason, it is impossible to consider all letters as unknown - there is not enough computing resources, which means there is no practical application. Calculation of the letter T takes 82 seconds per 3GHz Phenom. Of course, a direct enumeration of all unknown bits (256 values) would take a split second, so in this sense there is also no practical use for the program.
It seems to me that there is a possible way of optimization, which is to invent a compact record of sets, but still the method will not work faster than brute force.
Link to a project that finds the letter T: https://github.com/chabapok/sha256unroll
Source: https://habr.com/ru/post/217663/
All Articles