How Minkowski in Flappy Bird played

Many have tried to play Flappy Bird. Few who manage to fly over 50 pipes, very few reach a hundred or two. Some tried to create a bot, including on the habr . Surprisingly, even the most successful bot, which can be found on the Internet, the results are not very impressive - something about 160 points . The question arises, is it even possible to play Flappy Bird for a long time? Or is it always with a certain, albeit small, probability that a sequence of obstacles can meet, which even an experienced player / perfect bot cannot overcome?

And here mathematics comes to the rescue. Let's find a winning strategy for Flappy Bird.

Model

We describe the mathematical model of the game. Our playing field is a plane. There is a bird - a square with sides of length w parallel to the coordinate axes. There are obstacles - pipes - vertical stripes of width w _tube with horizontal openings of height h _gap . The distance between two adjacent obstacles is fixed horizontally and is equal to Δ _tube . The location of the horizontal opening for each pipe is random (evenly in a certain range). In addition, there is a floor - a horizontal line f. Sex is also an obstacle. Picture:
')


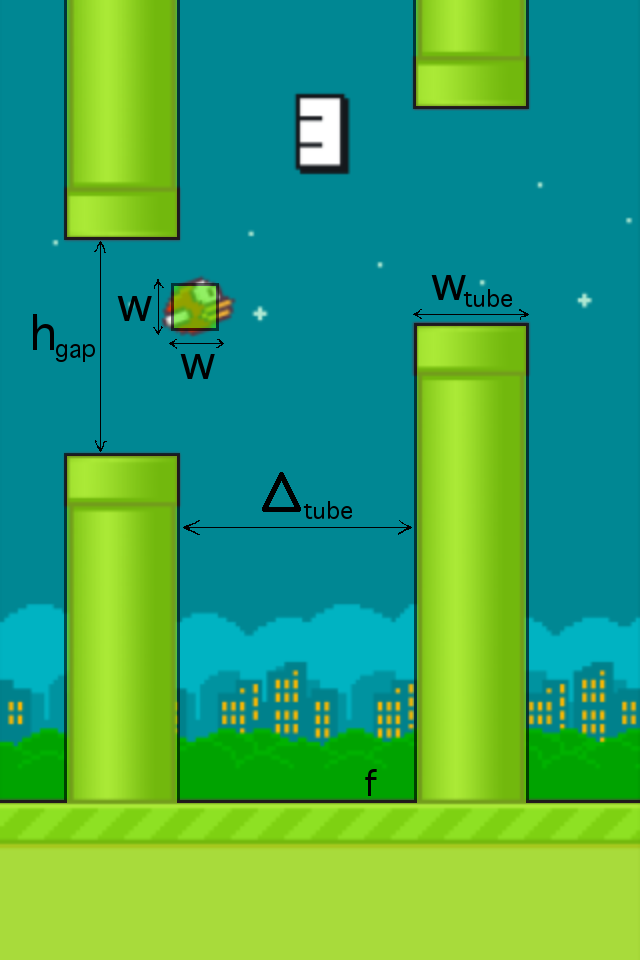
The speed of the bird horizontally constant and equal to v _x . Gravity also acts on the bird, giving it a vertical acceleration g. Initially, the bird’s vertical speed is 0. At any time, the player can make a tap, that is, make the bird’s vertical speed equal to v _jump . In addition, a kind of air resistance acts on a bird - its vertical speed is limited from below by a constant v _fall . In fact, this means that after each tapa the bird moves along a parabola, passing at some point into a straight line. The trajectory along which the bird moves after the tapa will be called the padabola (parabola of the fall). It looks like this:



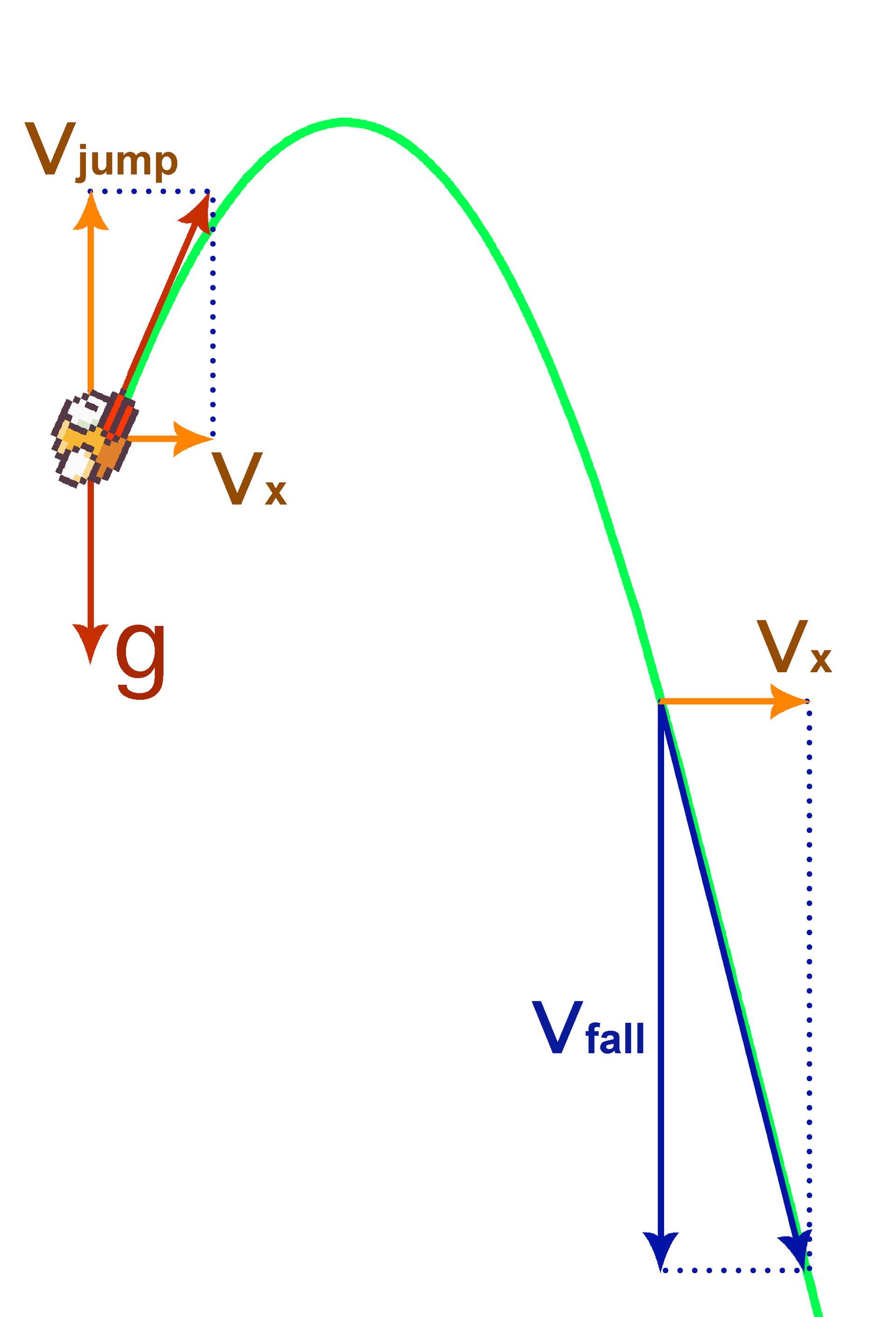
The game ends when the bird touches an obstacle. The task of the player is to maximize the distance traveled.

Before moving on to the passing strategy, let's do one trick. Analyzing the intersection of a square birdie with obstacles is not very convenient. But, it turns out, it is easy to move to an equivalent model in which the bird is a point. To do this, it is enough to “blow off” the bird to the size of a point (the center of the original square), at the same time “inflating” the obstacles. In this case, the initial square intersects with obstacles if and only if the new pinhole bird lies in the inflated obstacle. Picture:



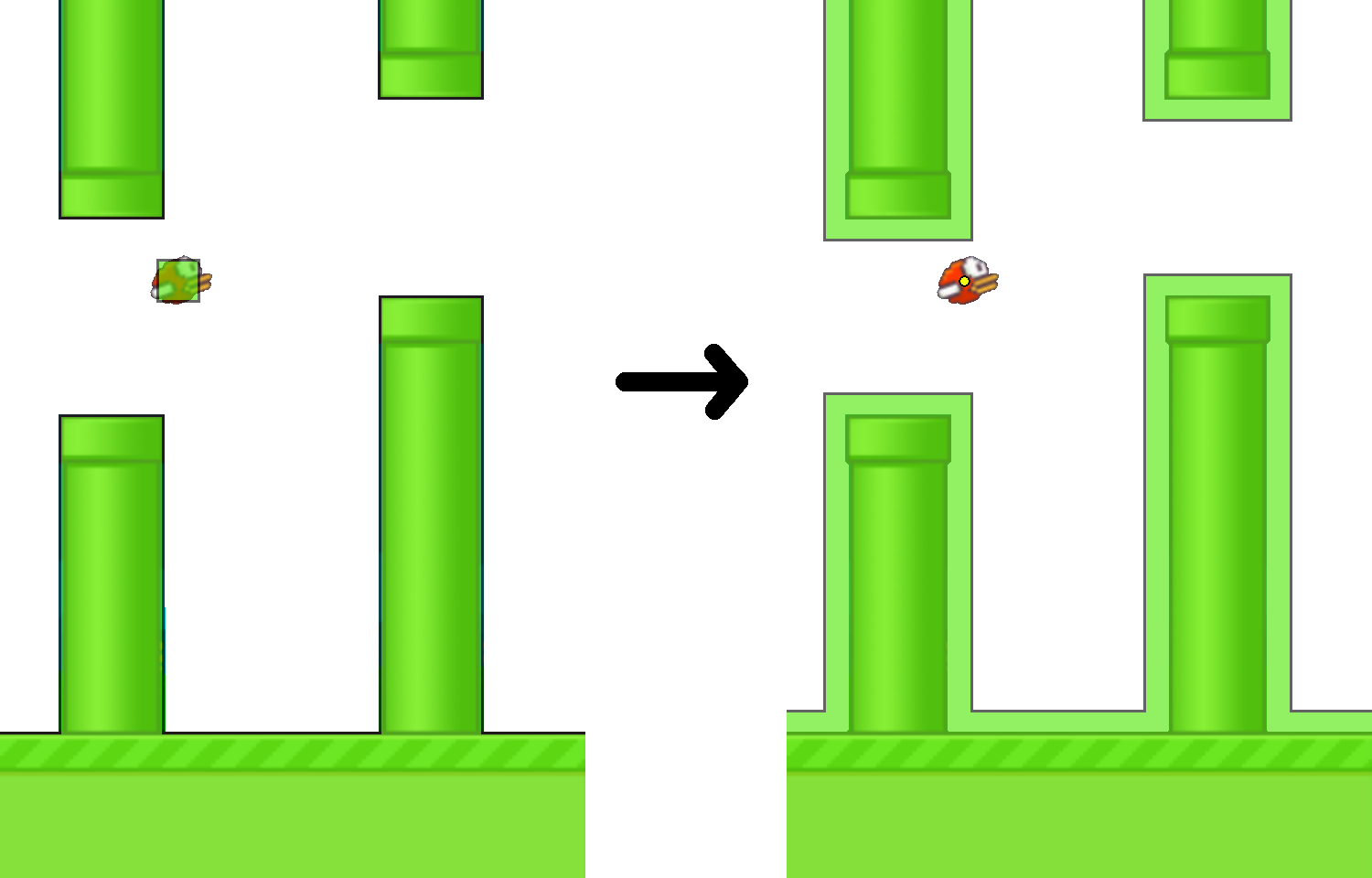
In a scientific way, the result of “blowing up” obstacles is called the Minkowski sum.

Minkowski amount

Wikipedia reports:

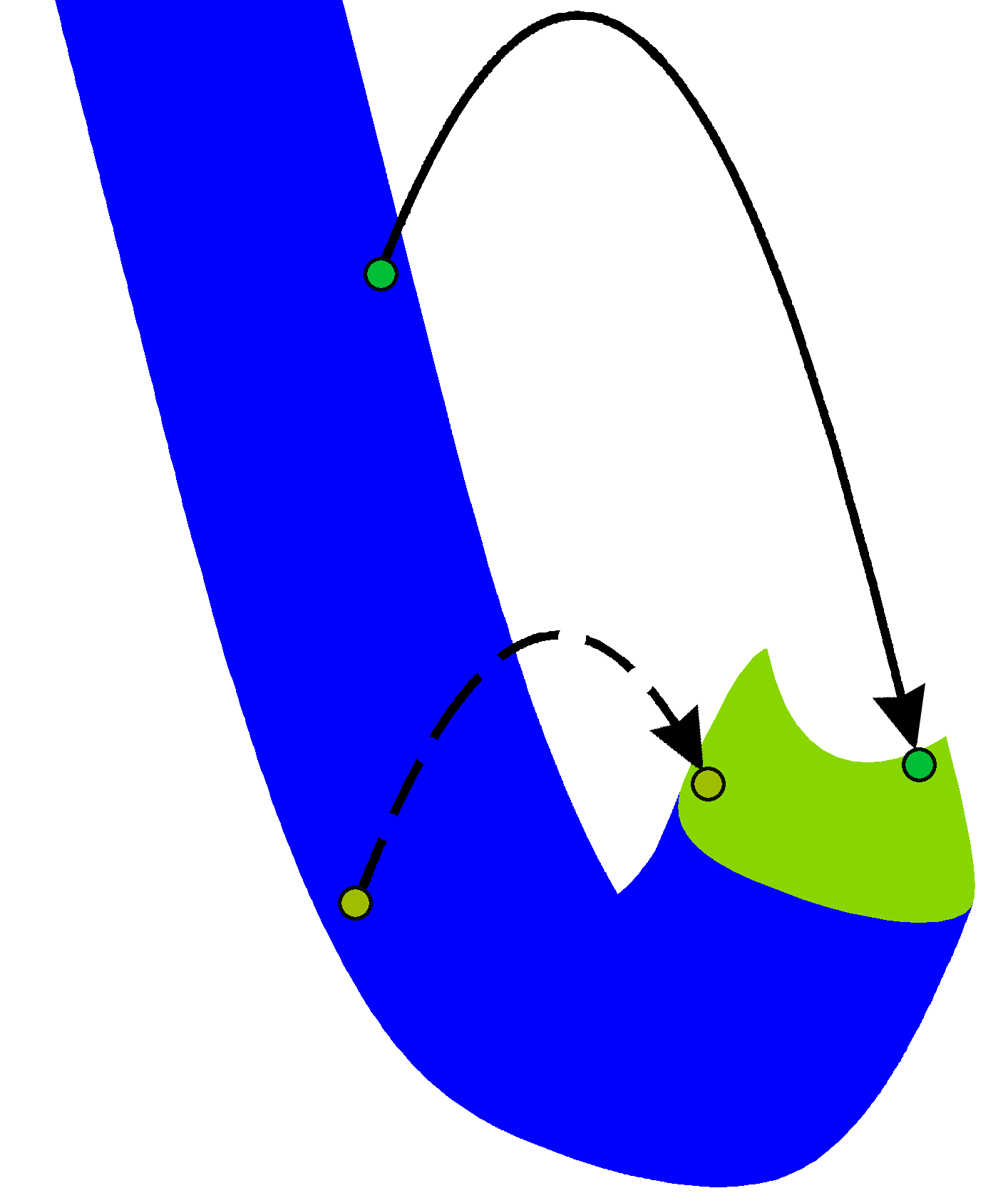
The Minkowski sum of two subsets A and B of a linear space V is the set C, consisting of sums of all possible vectors from A and B: C = {c | c = a + b, a∈A, b∈B}

From a household point of view, we can assume that the sum of Minkowski of figures A and B is a figure obtained by attaching a figure A to each point B - see the right figure.

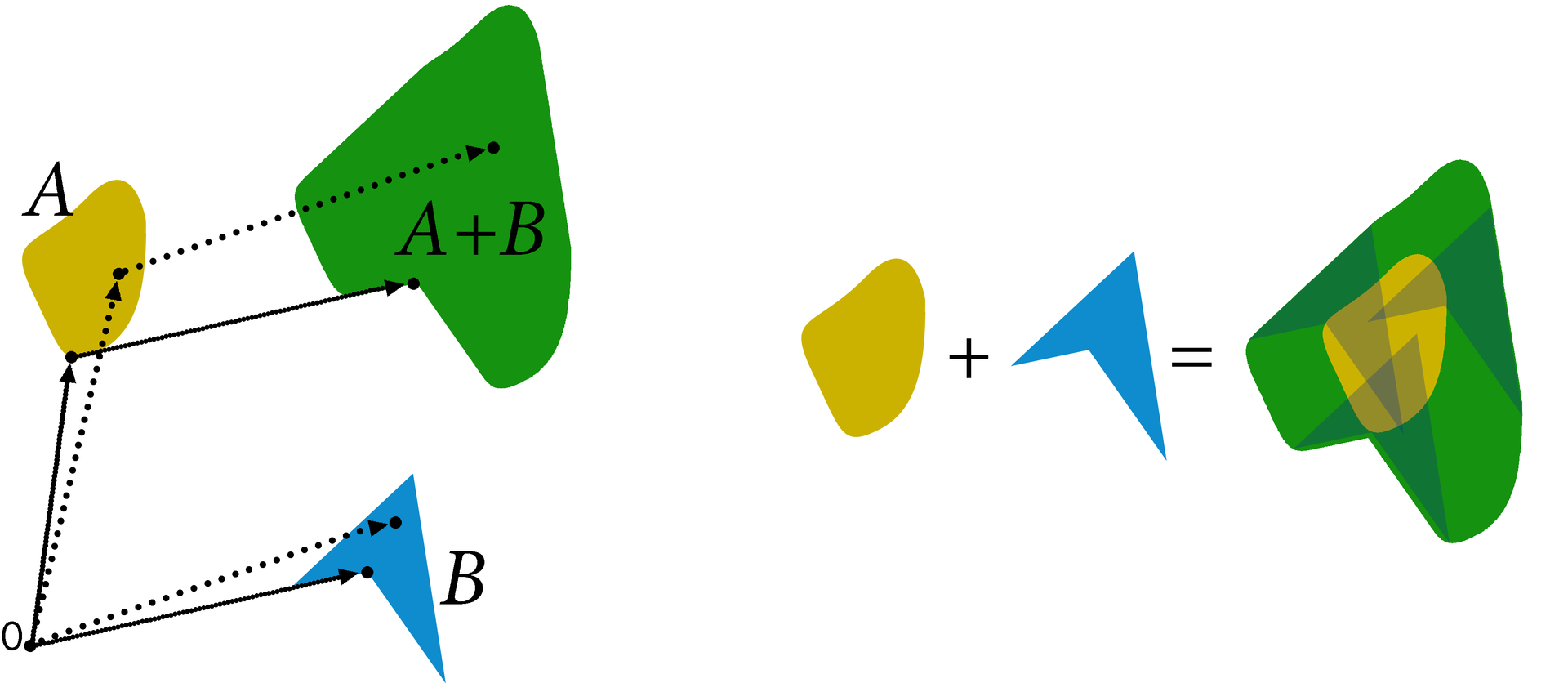
Reverse padabola

Let us solve an auxiliary problem: where should the bird be located, so that after the tapa it will fly through the given point A? More precisely, it is required to find the locus of points such that the padballs drawn from them pass through a fixed point A. See the middle figure. Let v⃗ be an arbitrary vector connecting the beginning of the padabola from one of its points. It is easy to see that after the tapa at point A-v⃗ the bird will fly through point A. That is, A-v⃗ belongs to the desired locus of points. Moreover, taking all possible vectors v⃗, we get all the desired points. But what is the set of points of the form A-v⃗, where v is the radius of the vector to one of the points of the padabola? This is the path centrally symmetric to the padball after reflection about point A. With the picture, by the way, it’s clearer:



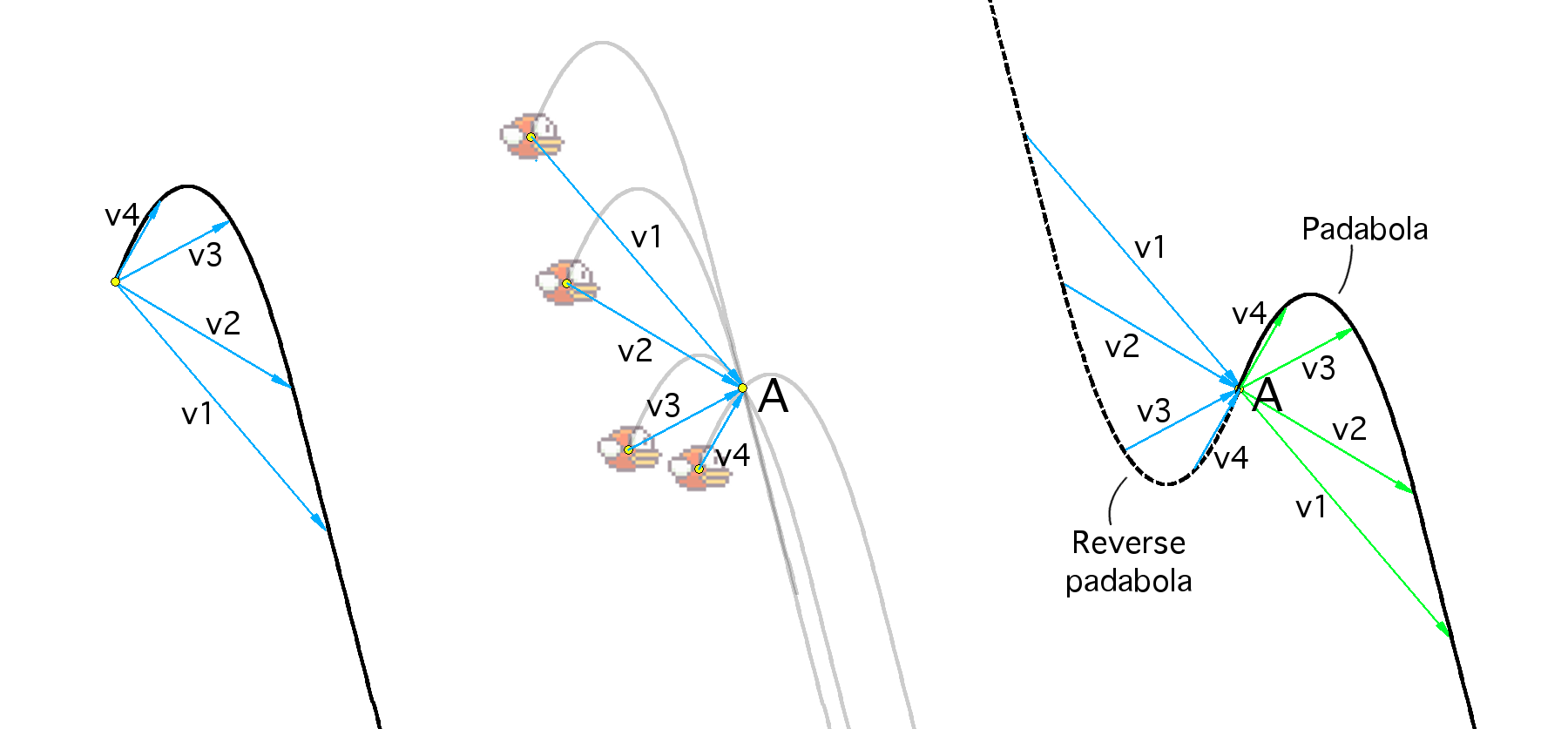
You can generalize the problem: where do you need to tap to fly through a given area S? Based on the foregoing, the answer is the sum of the Minkovsky region S and the inverse of the padball:

Top obstacles

Let us turn finally to the main task - finding a winning strategy. Only first we solve it in the simplified case. Suppose there are no lower halves of pipes and a floor in the model. That is, we have only the upper parts of the obstacles. Consider a free-standing upper half of the pipe. Let the bird start its way somewhere far to the left of this obstacle. Suppose at some point in time the bird crashed into a pipe. As we know from the previous section, this means that a tap was performed in the region obtained by adding a reverse padball to the obstacle. Color the resulting area in blue. Picture:



Note that if a player taps at a point in the blue area, then the corresponding padabola first crosses the obstacle and only then leaves the blue area. In other words, the player will be forced to either lose or tap again in the blue area. Well, since the separately taken blue area is bounded on the right, it will not be able to fly in it indefinitely, and in the end, the bird will die. Thus, tap in the blue region always leads to defeat. Moreover, tapas outside the blue area cannot lead to a loss - without a tapa in the blue area, you cannot hit the top obstacle, and there is nothing more to prevent the bird from flying.

As a result, for the case of top obstacles alone, we obtain the following statement.

Approval If the bird begins its flight outside the pool of blue areas, then endless winning strategies exist. And all winning strategies are described as follows: outside the blue areas the player can make arbitrary decisions, in the blue areas the player cannot tap.

Lower obstacles

Now consider the case when only the lower halves of the pipes are present in the model. That is, there are no upper halves and gender. Again, consider a detached lower obstacle. Draw an AC beam through its upper left corner (point A), the slope of which is atan (v _jump / v _x ) - that is, the beam directed along the speed of the bird at the moment immediately after the tap. Let the bird be below the AC beam. Then, regardless of the player's actions, she will not be able to rise with a vertical speed greater than v _jump . Given the constant horizontal velocity v _x, this leads to an inevitable collision with an obstacle, that is, a loss. Color the bottom obstacle and the area below the AC beam red. These are the red slides obtained:



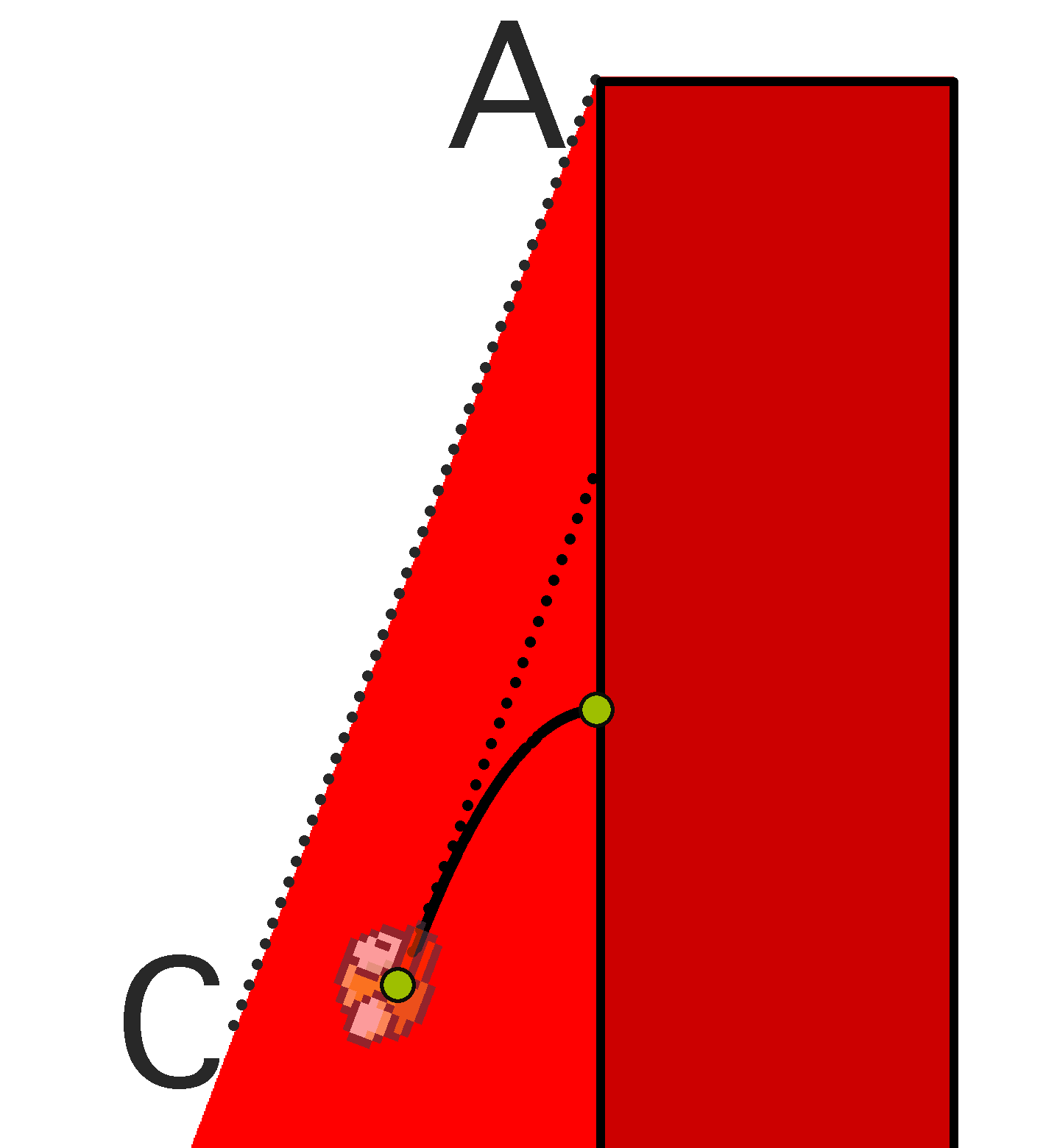
It turns out that for any winning strategy the bird should not fall into the red areas. Moreover, if the bird is out of the red area at some point in time, then it will be able to remain outside it indefinitely. Indeed, always when approaching the border of the red area, the player may begin to tap often enough not to be in it.

Add a floor. It is easy to see that the floor can be perceived as another red area in the form of the lower half-plane.

Thus, if only the lower obstacles and the floor are present, then it is true:

Approval If the bird at the initial moment of time is outside the union of red areas, then there are endless winning strategies. All winning strategies can be formulated as follows: outside the red area, the player can make any decisions, when approaching the red area, the player must tap.

All obstacles together

Consider the overall situation. Suppose there are upper halves of pipes, both lower and floor. The following is understandable:

Approval If the union of the blue areas does not intersect with the union of the red and the birdie is initially outside the blue and red areas, then there are winning strategies. Any winning strategy is described as follows: outside the blue and red areas, you can make any decisions, you cannot tap in the blue areas, and when you approach the red areas, you need to tap.

The absence of intersections of blue and red areas for the existence of such a strategy is essential. Indeed, it may happen that a bird flying through the blue area comes close to the red border - in this case, if the player taps, he loses, if he does not, he loses too.

The question arises, do the blue and red areas intersect in a real game? It turns out sometimes intersect. And it happens exactly in one case: when there is a sufficiently large drop in height between the openings of two adjacent pipes.



Let's analyze this situation. Let the bird manage to fly through these pipes. So, at some point in time, she crossed the segment AB. But this means that a tap was performed in the area between reverse padballs, drawn from points A and B. At the same time, this tap could not be produced either in the blue region or in the red one. Only the area shown in yellow remains.

That is, for the existence of a winning strategy, you must be able to guarantee that you are entering the yellow area. Then there will only be a tap and the dangerous area will be overcome. In order to understand whether we can always get into the yellow area, add it up with the reverse padabola - we get the area (green in the figure), which is enough to get in order to fly to the yellow one tap. We note that if at some point in time a tap is made at a point lying above the G line, we will not be able to get into the yellow area. And vice versa, for any point below this boundary, we can always, by tapping a sufficient number of times in a row, climb into the green area, then, by tapping once, hit the yellow one and, accordingly, overcome the obstacle. In other words, the points that are above the line D in our terminology should be painted blue. True, for the most part they are already blue, with the exception of the curvilinear triangle XYZ. To finish XYZ in blue. Now, to formulate a winning strategy, it remains to add the phrase: if the bird is in the yellow area, you need to tap at least once before the bird leaves this area.

Note that the finishing of the triangle in blue could not add intersections of red and blue areas, and therefore did not affect the analysis of the permeability of the game as a whole.

As a result, in the general case we get:

Approval Let the bird at the initial moment of time be outside the blue and red areas. Then there are endless winning strategies. All such strategies can be described as follows: outside the blue and red areas you can tap at any time; in the blue areas can not tap; when approaching red it is necessary to tap; once in the yellow area, you need to tap it at least once before exiting it.

Interestingly, the strategy of the species to begin the flight above a certain line and tap as soon as the bird descends to it (for example, it would be logical to take the upper limit of the red areas slightly shifted up) as such a line probably will not be for any line.

Practice

All this is good, but I would like some practical results. Hardwar bots on Habré have already seen, so we decided to make the software. Quite by chance, the code of our clone called Tappinator, whose physical model is close enough to the original game, turned out to be at hand - we tried and measured it. True, our bird is round (although it may be round in Flappy Bird, but the difference is not great, but it's easier to explain from the square one) and there are additional obstacles - inclined. This is how the obstacles for the round bird "swell up":



As a result, the blue and red areas we have are:



As for the yellow areas, they all also arise for standard pipes, but also arise in the case of oblique obstructions, directed from the bottom up (with their curved blue triangles and in general):



Well, actually, video with bots:



In the video you can see how 50 birds quite successfully reach 1000, how any colored areas look from the point of view of the bot and what the game would look like if 1000 birds flew at the same time. In unpainted areas, bots behave randomly: each of them has its own fixed probability of making a decision to jump at each moment in time. It can be noted that from the point of view of the bot, the colored areas are somewhat larger than from the point of view of mathematics. The fact is that a bot can only make a decision 60 times a second, and the physical model is also updated discretely.

Conclusion

So, it turns out, even in such a simple game like Flappy Bird, there is where to expand a mathematical theory. And in fact, the most interesting thing from this moment is just beginning. Then the question arises of how to deal with obstacles of arbitrary shape - here we have to introduce such concepts as purple shadow, burgundy border, right-linear-connected region, right-linear-connected closure, etc. It is also interesting what kind of reaction a person should have (that is, what is the allowable error in time with tapa he should have) so that he can play indefinitely. By the way, this is an extremely non-trivial question, the strict answer to which is still unknown to us.