Calculate the day of the week in the mind
There are many ways to pump the brain. N-back tasks or mobile apps for quick mind counting. But these tasks are divorced from the current reality, but I would like to pump the brain with a practical skill.What for? After all, you can quickly find on the gadget. Alas, not at all quickly, because It will take time to search for and activate the gadget, search for an application, enter a date, and realize the result. And you can also make friends / girlfriends happy with their suddenly extraordinary abilities. By the way, friends quickly realize the usability of the perpetual calendar with voice interface.
Is it possible? Somehow they did without computers. In one of the TV shows, “looking for talents” showed a trained three-year-old child who can calculate the product of three-digit numbers (spare your children). However, adults are no longer children and their brains are partially crystallized, in the sense of poorly trained. So you need to memorize as little as possible and maximize the existing skills.
In algorithmics, often the amount of computation can be compensated by the amount of memory. Those. the more RAM available, the less computation is required. The brain works the same way - the more we remember, the faster we look for a solution. We remembered several formulas for assembling the Rubik's Cube — assemble them in a couple of minutes (after a long workout). They remembered one and a half hundreds of formulas - collect them in a couple of tens of seconds. The world record of 2013 - 8.18 sec. Once again: the more we remember - the faster the solution.
')
Algorithm
You need to take the offset (day of the week) of the first day of the year (y) and the offset of the month (m). Then calculate the sum of y + m + d, where d is the day of the month, and find the remainder of dividing by 7. Get the number of the day of the week.
What you need to remember
Reflections
In general, it is enough to remember all the days of the week for all 28 years (periodicity is proportional to the product of periods of leap years and days of the week). The sequence in 10k. This is quite a lot.
If you add one addition operation, then it will be enough to remember only a couple of rows of numbers:
m (month) = {6 2 2 5 0 3 5 1 4 6 2 4}, from January to December
y (year) = {6 0 1 2 4 5 6 0 2 3 4 5 0 1 2 3 5 6 0 1 3 4 5 6 1 2 3 4}, from 1988 to 2015
For example: September 13, 2013 = (13 + 4 + 2)% 7 = 5 (Friday)
Offsets for the month are taken from the calendar of a certain year. The month offset is equal to the number of gray squares at the beginning of the month. For example, not a leap year 2006. The offset for this year will be 0.
Still, remembering offsets for all years and then performing a quick index search is a rather difficult cognitive task. There is an alternative way - to calculate. We need to take the last two digits of the year (+100 for the XXI century) - Y. Next, find the closest past leap Yv. Take dY = Y - Yv. Then the year offset can be calculated
y (Y) = (50 - Yv / 2 + dY)
The disadvantage of the formula is that for 2004 and further the bias will be negative, and for the beginning and the middle of the XX century two-digit, which makes it difficult to calculate in the mind. You can use different formulas for each century, which take into account only the two lower digits of the year. For example, 12 for 2012 and 1912.
If you add one addition operation, then it will be enough to remember only a couple of rows of numbers:
m (month) = {6 2 2 5 0 3 5 1 4 6 2 4}, from January to December
y (year) = {6 0 1 2 4 5 6 0 2 3 4 5 0 1 2 3 5 6 0 1 3 4 5 6 1 2 3 4}, from 1988 to 2015
For example: September 13, 2013 = (13 + 4 + 2)% 7 = 5 (Friday)
Offsets for the month are taken from the calendar of a certain year. The month offset is equal to the number of gray squares at the beginning of the month. For example, not a leap year 2006. The offset for this year will be 0.
Still, remembering offsets for all years and then performing a quick index search is a rather difficult cognitive task. There is an alternative way - to calculate. We need to take the last two digits of the year (+100 for the XXI century) - Y. Next, find the closest past leap Yv. Take dY = Y - Yv. Then the year offset can be calculated
y (Y) = (50 - Yv / 2 + dY)
The disadvantage of the formula is that for 2004 and further the bias will be negative, and for the beginning and the middle of the XX century two-digit, which makes it difficult to calculate in the mind. You can use different formulas for each century, which take into account only the two lower digits of the year. For example, 12 for 2012 and 1912.
XX: (50 - Yv / 2 + dY)% 7 or (8 - Yv / 2% 7 + dY)
XXI: (7 - Yv / 2% 7 + dY)
As a result, it may be easier to remember the offset table in the following form:
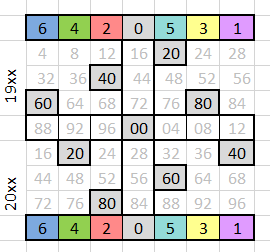
The offset for the year can be calculated by the sum of the offset of the nearest smaller leap year and its difference with the desired year. Seven digits are easier to remember than 28. In addition, the digits are arranged in descending order in increments of 2. (Yes, yes, (0 - 2) will be 5, remember the remainder of the division by 7). You can remember the numbers (6, 4, 2, 0, -2, -4, -6), which will give a similar result in the calculations. Years multiple 20 are located in an oblique square 3x3 according to the scheme "knight's move" c 2000 in the center. The values ​​of the offsets of months and years are agreed so that in 2000 there was a shift of 0. And the step between adjacent rows is 28 years.
For example, for 2014, the offset will be y (2014) = y (2012) + 2 = 1 + 2 = 3. And the day of the programmer on September 13, 2014 will be (y (2014) + m (Sep) + 13) = (3 + 4 + 13) = 20 => 20% 7 = 6, i.e. Saturday.
We structure the number of offsets for months. The values ​​are conveniently memorized by the seasons: spring, summer, autumn, winter.
Note that suddenly (?), In order from top to bottom and from left to right, the numbers are lined up in a rising row (the first color table). You can memorize only the remnants of division by 7 (the second color table) or to restore the entire table, remember only the differences (the last table). Adding 1 to 1, we get for March 2, for June 2 + 1 = 3, for September 3 + 1 = 4, etc. The same values ​​are painted in the same color. For a quick search will help us the second color table. Remember that lines are seasons, starting in spring. This is extremely unusual. But in ancient Rome, the year began with March. This is reflected in the names of the months in Latin numerals: Septem ber / Octo ber / Novem ber / Decem ber - 7/8/9/10, i.e. February was the last 12th month of the year, to which a leap day was added.
April 12, 1961: (6 + 1 + 5 + 12) = (0 + 5 + 12) => 17% 7 = 3 - Wednesday.
Important!!! Programmers have an eternal problem with a lost unit. In our problem, this has not been done without. For January and February of a leap year, you need to subtract a unit.
February 14, 2012 = (y (2012) + m (Feb) +14) - 1 = (1 + 2 +14) - 1 => 16% 7 = 2, i.e. Tuesday.
It is also necessary to remember that not all years that are divided into 4 will be leap years (exceptions - 2100, 1900, 1800, ....). Accordingly, it is necessary to consider the offset for the century. However, even if you do not take into account the last exception, you can unerringly operate on days of the week for the XX and XXI centuries, which is enough for most everyday cases.
A bit of optimization.
Calculations can be performed in streaming mode. Usually, the date of birth (or any other date) is reported starting on the day of the month, for example, December 23, 1913. Those. In the process of reporting the date, you can partially calculate the desired amount of 23 + m (dec) = 27 or even 23% 7 + m (dec) = 2 + 4 = 6 and then think about y (1913) = y (1912) + 1 = 3 In the end, report 30% 7 = (6 + 3)% 7 = 2, Tuesday.
Often it is necessary to operate on the dates of the current year. Those. the year offset you will always remember from frequent use, the value is "cached". For example, for 2014, the offset is 3.
What we got. The rules for filling in the tables are simple and you will most likely remember them and will be able to reproduce yourself a cheat sheet anywhere at any time. But for quick counting the table is easier to memorize entirely. After all, we do not restore the tables of addition and multiplication to calculate the change in front of the cash register. These tables are “stitched” in elementary school. The easiest way to memorize tables is to use the Week Brain Calc (Windows Phone).
After a short workout, you can please your loved ones with your unique abilities.
Source: https://habr.com/ru/post/217389/
All Articles