The logic of thinking. Part 17. The relational data model.

This series of articles describes a wave model of the brain that is seriously different from traditional models. I strongly recommend that those who have just joined begin reading from the first part .

In 1970, Edgar Codd published an article (Codd, 1970) in which he described the basics of the relational data storage model. The practical implementation of this model has become all modern relational databases. The formalization of the model led to the creation of relational calculus and relational algebra.
')
The main element of the relational model is a tuple. A tuple is an ordered set of elements, each of which belongs to a certain set or, in other words, has its own type. The set of homogeneous tuples in structure forms a relation.



Somewhat more clearly, all this looks in terms used in databases (figure below). A relation is a table with data. A tuple is a row of a table. What type of tuples are contained in a relation, or, equivalently, what is the format of the rows in a table, is determined by the relationship or table header. Each of the columns in the table forms a domain. Values ​​that domain elements can take are called attributes. Table rows are a collection of attributes corresponding to domains.


Relationship Example (Fences)

The rows of the table can be identified by their attributes, that is, by what values ​​the elements of the tuple take. The content of the tuple itself makes it different. But it may happen that some strings match in their attributes. In itself, coincidence is not terrible, but it no longer allows using such a set of attributes to uniquely identify tuples in a relation. To make identification unique, a key field is introduced that takes a unique value for each line. Such a key can carry a meaning, or it can be simply an artificially generated number.

The totality of all relationships defines a database. Each relation stores its logical part of information. To obtain certain information, it may be necessary to map information from different relationships. Codd described eight basic operations of relational algebra, allowing manipulation of tuples:

• Union;
• Intersection;
• Subtraction;
• Cartesian product;
• Sample;
• Projection;
• Compound;
• Division.

The remarkable property of relational algebra is its closure, that is, operations on relations are defined in such a way that the result is itself a relation. That is, having several tables and making the corresponding operations on them, we get the result is also a table.

The meaning of many operations coincides with the corresponding operations from set theory. A general idea of ​​their essence is given in the figure below.


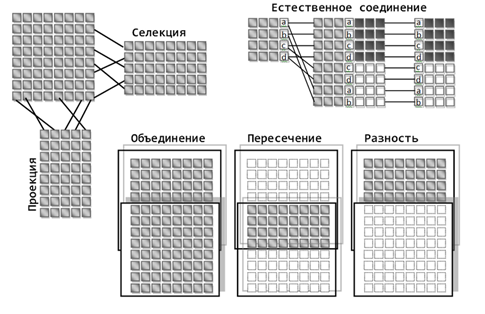
Example of tuple operations (Zaborov)

It is important that different relationships may contain domains of the same type. This means that if there are identical domains in two tuples, inside them there are identical attributes, then we can talk about a definite connection between the tuples containing these attributes. In other words, if different rows of the same table in one of the columns have the same values, then we can talk about a definite connection of these rows. Or if in different tables there are columns (domains) with the same meaning, then the rows with the same values ​​in these columns are interconnected.

The projection operation allows to obtain relations consisting of a part of the elements of the original relations, limiting the set of used domains. Sampling or selection allows you to get relationships that contain only those tuples whose fields satisfy the conditions of the sample. For example, you can select only those tuples whose specified domains have specified attribute values.

The combination of all operations on relationships allows you to extract from the database any information of interest and form it in the form of a relation (table) with predefined properties (header).

The relational data model did not arise by chance, but was a consequence of the need to operate with large volumes of diverse data. It turned out that such a data storage structure and operations defined in this structure are convenient for solving a wide range of applied tasks. It can be assumed that a similar successful solution could be groped by nature as a result of natural selection.

The system of identifiers, concepts and event memory described by us is very similar to the relational model in many respects. You can bring a number of analogies:

• The neuron operates with information from several dendritic segments, each of which is tuned to data of a certain type. Dendritic segments of the same type can be mapped to a specific domain;
• Combinations of concepts that describe information characteristic of a dendritic segment correspond to the attributes found in the domain;
• The concepts used by the cortex zone and the identifiers that define the packet structure characteristic of this zone define the domain structure (header);
• The use of common concepts in the projection of information between zones corresponds to the use of common domains in different respects;
• The set of cortical zones that form the brain corresponds to the set of relations that form the database;
• Associativity, between memories, corresponds to connectedness through the common attributes of different tuples;
• The distribution of memories across the zones of the cortex corresponds to how a single event can produce several tuples in different respects, united by a single unique key;
• A wave describing the current state of the brain can act as an analogue of a database request. Just as the result of a relationship operation is a relationship, so the response of the brain can be a combination of associatively related descriptions combined in one wave pattern.

Of course, there is no exact match between our brain model and relational systems. The brain architecture is much richer, since it solves not only the tasks of data storage and retrieval, but also a lot of other functions combined with it. However, even the existing similarity allows us to better understand the essence of the information processes occurring in the cortex.

References

Continuation

Previous parts:
Part 1. Neuron
Part 2. Factors
Part 3. Perceptron, convolutional networks
Part 4. Background Activity
Part 5. Waves of the brain
Part 6. The system of projections
Part 7. Human-computer interface
Part 8. Selection of factors in the wave networks
Part 9. Patterns of neuron detectors. Reverse projection
Part 10. Spatial self-organization
Part 11. Dynamic neural networks. Associativity
Part 12. Traces of memory
Part 13. Associative memory
Part 14. Hippocampus
Part 15. Memory consolidation
Part 16. Batch presentation of information

Alexey Redozubov (2014)