Search for solutions for games with words. Boron application

Introduction

There are many games where the player needs to search for words from a specific set of letters. Here are the two most popular ones.
1. 4 pics 1 words (4 Pics 1 Word) AppStore , Google Play
This game has quite a few implementations, but the idea is the same for everyone.
2. Slovomaniya (Wordsmania) AppStore , Google Play


The essence of the first game: 4 pictures are given, the length of the guessable word and a set of letters, you can choose the letters in any order.


')
The essence of the second is that in the 4x4 field, filled with letters, it is necessary to find as many words as possible, from each cell you can move to the next one vertically, horizontally, and diagonals.



I was interested in the idea of ​​software problem solving, which put these games. I do not set goals to make the game dishonest, it is rather a purely sporting interest in the task set to itself. The peak of the popularity of these games has already passed, so it's not so scary if someone plays a little dishonestly.

Formulation of the problem

If we consider the problem more formally, it is necessary to implement a search of possible combinations, based on the rules of the game. Two brute force algorithms will be implemented for each game. Next, you need to check the presence of these combinations in the dictionary, for this you need to implement a structure that can effectively respond to the query about the presence of a word in the dictionary. Bor will be used.

Why bor

In the standard C ++ libraries, structures that can quickly respond to single requests are already implemented, these are map and unordered_map (hash map). But the implementation of the problem with the help of these structures will be inferior in the asymptotic behavior of boron, since it will take into account the peculiarities of the task. The enumeration of values ​​will be a tree, because recursively from each letter will try to find the next one. Bor is also a tree, so the search for words will take place in the worst case for the total length of all found words, plus the number of iterations, until the algorithm reaches a non-existent transition in the dictionary, in practice such a transition is achieved rather quickly. More efficiently, the algorithm will work when there is an S string containing the string P belonging to the dictionary as a prefix, in which case the search will take place beyond the length of S, and all the other P will be added to the answer during the search S.

Next, you need to display the resulting words in sorted form.

Implementation

Consider the implementation of the solution of the problem in parts.

Inclusions

It is necessary to provide console and file input-output, iostream, fstream. We need standard STL templates: vector - to build boron, string and set - to store the results and cut off the same words found, the algorithm to sort.

ads

In order to use Russian characters, without including localization, so that such code could be easily adapted to other encodings, it was decided to use a simple string pattern for input and output. This is a sample obtained by typing the ConsoleSample into the console of the Russian alphabet and a sample obtained by reading from the FstreamSample file.
Next, there is a description of the structure for each vertex of boron, it will store transitions for each letter, or 0 if there is no transition, also using the isLeaf variable in the structure indicates that any word ends at this vertex.
We declare containers for storing boron, a buffer for results and formatted output.

Adding words to bor

The function receives a string at the input, traverses it, simultaneously advances along the forest, if there is no transition from the vertex, a new vertex is added to the boron, and a transition to the added vertex is written to the current vertex using an index. After adding the last transition, the value of the isLeaf variable at the last vertex changes to true, here the word ends.

Dictionary Download

For convenience, all words will have their characters shifted by the time they process the request, that is, the character 'a' will match the value 0, and the character 'I' will have a value of 32. The Encode function will do this using a trivial search for a character in the sample and replace it . Such an implementation is simple, but it takes extra time to load the dictionary, but this is not so important, the dictionary is loaded one time, and then you can submit requests to the program many times.



The dictionary loading function retrieves the file name and reads all the words from it, encoding the lines and then adds them to the bor. The function can load several dictionaries at once if run for all files.

Sort output

To get the longest words in the game Slovomaniya first of all, you need to sort the lines by length in the reverse order, since when outputting to the console, the text is scrolled upwards, so the longest words should be output at the end. In the game, the bigger the word, the more points are obviously given for it. To do this, write the simplest comparator function to transfer it to the sort from the algorithm.

The implementation of the solution for the game "guess the word"

Since there are a lot of implementations and names for this game, we’ll just call it “guess the word”.
For starters, the bypass function is boron. Here we use the usual recursive DFS algorithm, just from each letter, we move to any unused previously from the given string, at the same time, we check for such a transition in boron, if the transition exists, then continue further, if not, stop further progress on this thread. It is important to note that in the game it is necessary to guess a word of a certain length, therefore we descend only to a depth equal to the length of the line, there is no sense to go further. We do not forget to check the isLeaf variable at each iteration, if it is equal to true and the length of the found word is equal to the specified value, then we add the word to set Res.



And then the function that implements the initial launch of the tour from all the letters of the word.

Implementation of the solution for the game Slovomaniya

In general, the detour itself will not be anything different, but the differences will be that here it is possible to move only to neighboring cells, and not to any, also the search should find words of any length. Since a 4x4 field is represented by a one-dimensional array, it is not obvious how to move to neighboring cells, consider how to implement it.
If the cell is not on the field borders, then by adding numbers from -5 to 5, excluding from them -2, 0 and 2.



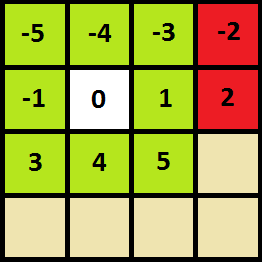
If the cell is on the border, then it is also necessary to prohibit transitions to other cells that go abroad.

Main function

In the main function, bor is initialized and the main loop is executed in which requests are processed. '1' or '2' as the first argument, depending on which algorithm to use, then the parameters for the algorithm. After processing, sorting and displaying results. For the first algorithm, you must enter a sequence of characters and then the length of the word, for the second, only the sequence, it is written along the lines of the field, that is, for such a field, you must enter the string "set the string" (without quotes).

What's next

Here is the full code , it is tested under Windows, for other platforms, you may have to replace input and output samples.
But the dictionary is small and large dictionary (do not forget to remove the number 2 at the end of the name if you will use a large dictionary). The large dictionary contains not only the initial forms, it is suitable for the game Wordament from Microsoft, but there is not always on the field is one letter in a cell. In most cases, a small dictionary is enough for the two games described to be at the top of the standings.



I hope no one will play a lot this way, yet most of the players continue to play fair.