VK Friendly Link Analysis with Wolfram Mathematica

Not so long ago, the Wolfram Research Era of Wolfram Technologies was held in Moscow, where they told a lot of interesting things about one of the most powerful and definitely the most convenient computer research system Wolfram Mathematica . In particular, the results of the study of data from the social network facebook by the Constructive Cybernetics research group were presented. A little earlier, I came across a new feature of Wolfram | Alpha for a comprehensive analysis of the facebook page . And after all this, I have a crazy idea stuck in my head: "I want to see the graph of friendly relations of the social network in which I live (namely, VKontakte) . " And I still found the time to implement it. Welcome under cat.





The interaction with the VK API begins with the creation of a Standalone application at https://vk.com/dev (in the same place, you can edit an already created application). After a few clicks and much thought over the name, the system issues the application ID that will be used to get Access Token .

To get Access Token , you need to follow the link below, replacing the grid with the application ID . How the line is formed, you can read here .



https://oauth.vk.com/authorize?client_id=######&scope=friends&redirect_uri=https://oauth.vk.com/blank.html&display=page&v=5.16&response_type=token



After that, a lot of useful information will appear in the address bar, in particular, access_token and user_id . These two values ​​need to be saved. I called the variables myID (Integer || String) and token (String).

The next step is to write a basic function that interacts with the API. The standard response format from VK API is JSON , which can be easily parsed into lists and rules by internal means of Mathematica .

')





The list of methods that are now available is limited only by the value of the scope parameter, which was passed during the formation of Access Token . To check the performance of the system, you can find out your name







The VK API output contains a lot of excess, therefore, in order to extract only useful data, you must first cut off the excess







And, then, apply replacement rules (and this is a list of replacement rules) to those parameters that are interesting. The remaining rules are automatically ignored.







Thus, you can write a module that receives the user name and (optionally) his photo







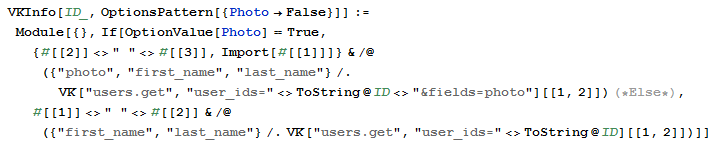
Note that the parameter for the API is called user_ids , not user_id . This will allow you to get information about the whole list of users for a single request (IDs must be separated by commas and must be less than 1000).



Now you need to find users who are interested in finding out something. Get a list of friends. In general, the whole function is as follows.







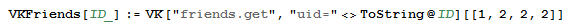
But due to my desire for idealism and the desire to at least a little closer in thought to the built-in functions of Mathematica , my VKFriends grew up here







However, the “ Clean ” version will be used to build the graph. The following is interesting here: if the fields parameter is removed, then the response from the API will be a list of IDs and nothing more. And if fields at least something is equal, the user name is automatically included in the response. Therefore, for the version without avatars, the value fields = sex is applied simply because sex is a beautiful word. In practice, the replacement rule for the floor in the final version is not implemented. Although you can always add fields that you are interested in exploring with your friends and building beautiful histograms of them, but then the code will grow many times and its structure will need to be changed (if, of course, striving for mass character).



The last function that is needed from the data collection API is mutual friends. With their help, it will be possible to explore communications only within your social circle, without receiving and processing megabytes of extra information about who your friends from those whom you do not know know. To bring the syntax and capabilities in line with VKFriends , we had to sweat a little. The fact is that friends.getMutual can only return a clean list of IDs, which is not obvious (if suddenly someone needs clarity)







Everything! On this integration with VK API for this task is over (and so much more than you have done). It's time to take the bull by the horns lists by the tails. Go!







We receive the list of friends, we describe communications. All of them are related only to you. The speed of performance - blink of an eye.







But do not worry, the time to go for tea and even you will have to drink it. Friends.getMutual itself is not particularly fast, so it must also be carried out for each of your friends. On my 333 friends, it took 119 seconds. This is the longest operation for the entire study. While this function works, you can put the kettle on and choose tea. DeleteCases appeared in the process of debugging, when the depth of the resulting array was suddenly equal to 7. And all because there are users in friends for whom, for some reason, mutual friends are not available. And the error message is presented in the form of rules. Therefore, removing all the rules, the depth of the array will become normal, and the data type will become Integer (represented as a String).

As a result of the code execution, the friendsOfFriends variable will have a two-dimensional list, the size of Length [myFriends]. And each element of myFriends (friend) will correspond to a list of your mutual friends with this friend. Now you need to connect each friend from myFriends with all his friends from friendsOfFriends . Fuh. It seems to explain it with words, but if you use an embedded Map for this, it will turn out to be completely unreadable. Therefore, we cheat a little in a procedural style (kindly requested not to repeat on our own. This is a very bad style for Mathematica. The assembler was based on goto and in procedural programming it became a bad style, and the Wolfram Language allows you to solve everything analytically, and here the explicit style is explicit cycles [ purely formally this makes it the language of a new generation])







Next, you can try to build this graph, but nothing will come of it. Non-oriented graphs with the degree of vertices greater than one are added only in the not yet released Mathematica 10. The degree of all the vertices of a non-digraph is two, for each user who is in friends with another user is also in friends with the first. Simply put, we found a common friend B with user A, and when we looked at page B, user A also finds himself in mutual friends. And after examining the entire network, all users began to connect with two edges. To see this, replace UndirectedEdge with DirectedEdge for all entries. But the digraph is redundant exactly 2 times, so it is necessary to get rid of repeated edges and build an undirected graph.







I had to write my own checking function, because I don’t have one. And, for one thing, combine the graphs together. Strangely enough, it works for quite a long time ... As a result, the number of links should decrease slightly less than twice, because the links from gMyFriends are not duplicated.

All right, you can build! Only nothing will be clear. So we continue to code until it becomes clear.



In order to become clear, it is necessary to change the type of graph vertices. This can be done with the VertexShape option of the Graph function. VertexShape accepts a list of rules for replacing names with any objects. The names of the vertices in this case are a list of gMyFriends , extended with just one element - the user myID . Thus, it is necessary to obtain information for all the elements of the list [[myFriends, myID]] and make this rule out of it. Remember the boiled teapot? It's about time. You have a couple of minutes to drink tea.







What is cool is that all the infa is requested immediately in one request. Only it is necessary to remove parentheses and spaces from ToString@Append[myFriends, myID] .

Now we have an array of what needs to be replaced and an array of what needs to be replaced. But no, not yet. You need everything to be beautiful.







First, rectangular frames with the name and avatar are constructed, then they are placed in a three-level list next to the corresponding IDs, and then in each list item from the lists, the function header is replaced from List to Rule. As a result, we get a list of rules from the list of lists. (Well, isn't Wolfram Language beautiful?)



Now everything is exactly!







You can enjoy the result. Personally, I managed to export this beauty only to PDF, however, the Cyrillic alphabet disappears, so if your page is Russian, add to the VK function " &lang=en " after " &v=5.16 ". My result looks something like this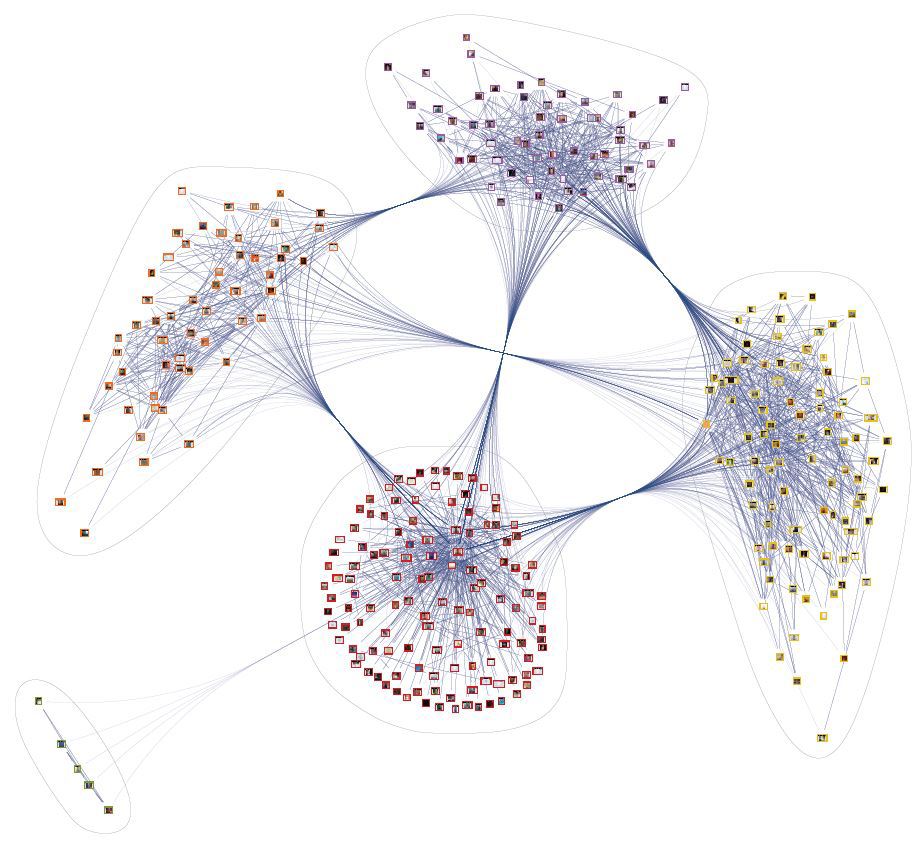









Impressive. Globally. Especially when contact is the primary means of communication.



Download notepad here . More than 300 people in one request no longer pass; it is necessary to share more on this later.

---

(A week has passed)



Today they proved to me that it is useless to draw myself on a graph, because in any case you are connected with each of your friends with one connection. Therefore, this connection is redundant. I rebuilt my graphs and they have changed. Also, I added a mechanism to automatically split the list of friends into parts and collect the result. Now it even shows the progress of the execution - after each request it prints a line and when the lines printed are as many as the parts in the divided list of friends, this is 100%.







It was experimentally determined that if there are more than 200 people in one request, problems begin. The optimal amount is 100. In general, the smaller, the more reliable. I have 50 because 300 friends in total.



And yet, I had to throw out from friends all who have no common. They are carefully displayed on the screen and are excluded from further calculations.



All this is available here.