Training / gaming program for calculating the payload of the rocket based on several stages and gravitational losses

It is believed that in the optimal layout of a multi-stage rocket, each stage should have a characteristic speed margin (delta-V) of 4 km / s. It is believed that the optimal initial thrust-to-weight ratio is 1.2. But these ideas need to be confirmed somehow. I also wanted to visually show why rockets are multistage. Formulas are good, but something else is needed, and games and competitions are perfect as such. Thus was born the project of an educational / gaming program, code-named "enlarge your MON "

Problem statement and accepted simplifications

It seemed to me uninteresting to virtually rocket a rocket in a vacuum away from the planets. Therefore, the task will be to start from Earth. The calculation of the aerodynamic drag and the exit into orbit from the surface presented itself as complicated, so the rocket, as in Newton's mental experiment, will start from a “high mountain” in a vacuum:

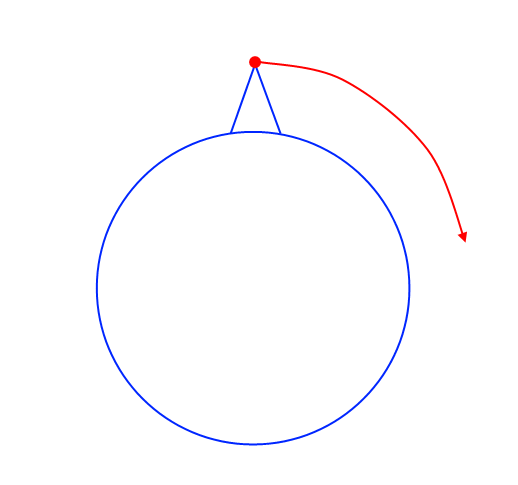
Input parameters

The following parameters were selected as input data:

• Dry weight of engines, kg
• The number of engines, pieces.
• Traction engines in kilonewtons.
• Consumption of all components of fuel by one engine, kilogram per second.
• Mass of fuel, kg

Calculated and related parameters

Those who are at least slightly interested in rocket technology may ask where the specific impulse that is used in the Tsiolkovsky formula has disappeared? In fact, he has not gone anywhere. The specific impulse is implicitly contained in the engine thrust and fuel consumption. UI is proportional to the load and inversely proportional to the fuel consumption. The more traction and less fuel consumption, the more UI.
The engine thrust in tons can be converted into thrust in kilo-newtons by multiplying it by 9.81.
The mass of tanks, adapters and other auxiliary structures is considered to be “offhand” as 10% of the mass of fuel and is called “parasitic mass”. This is a rather serious simplification, because in reality this parameter strongly influences the overall effectiveness of the rocket and differs from one rocket to another. The lighter the tanks, adapters and other structures, the less parasitic mass it is necessary to lift the rocket.
Total and empty masses are calculated based on known parameters. Empty mass is the mass of all engines and parasitic mass, the total mass is the empty mass and mass of fuel
The calculation of gravitational losses is shown in detail below.

Parameters not considered

• To simplify the tasks are not considered:
• Friction loss on the air.
• Change thrust depending on atmospheric pressure.
• Climb.
• The loss of time for the separation of steps.
• Changes in engine thrust at the site of maximum velocity head.
• Only one layout is taken into account - with a sequential arrangement of steps.

A bit of physics and mathematics

Speed ​​calculation

The acceleration of the rocket in the model is as follows:

Flight altitude is assumed to be constant. Then the rocket thrust can be divided into two projections: Fx and Fy . Fy should be equal to mg , these are our gravitational losses, and Fx is the force that will accelerate the rocket. F is constant, it is engine thrust, m varies due to fuel consumption.
Initially, there was an attempt to analytically solve the equation of motion of a rocket. However, it was not crowned with success, since the gravitational losses depend on the speed of the rocket. Let's conduct a mental experiment:

1. At the beginning of the flight, the rocket simply does not come off the launch pad if the thrust of the engines is less than the weight of the rocket.
2. At the end of the acceleration of the rocket, everything is also attracted to the Earth with a force of mg , but this is unimportant, since its speed is such that it does not have time to fall, and when it enters a circular orbit, it will constantly fall to the Earth, “missing” by it from for speed.

It turns out that the actual gravitational losses are a function of the mass and speed of the rocket. As a simplified approximation, the gravitational losses I decided to consider as:

V1 is the first cosmic velocity.
To calculate the final speed had to use numerical simulation. In one-second increments, the following calculations are made:

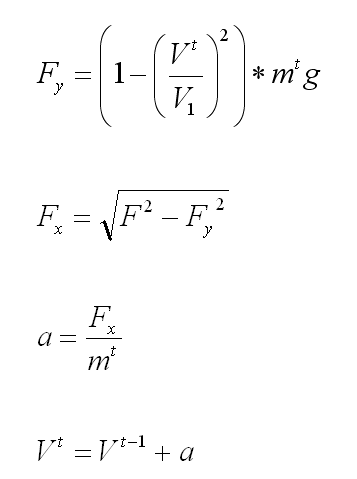
The superscript t is the current second, t-1 is the previous one.

Calculation of the maximum payload

Knowing the final rate for each allowable payload, you can solve the problem of maximizing the payload as the problem of finding the root of a nonlinear equation.

It seemed to me most convenient to solve this equation by the method of half division :

And play?

Now, after the theoretical part, you can play.
The project is located on GitHub . MIT license, use and modify for health, and distribution is even welcome.

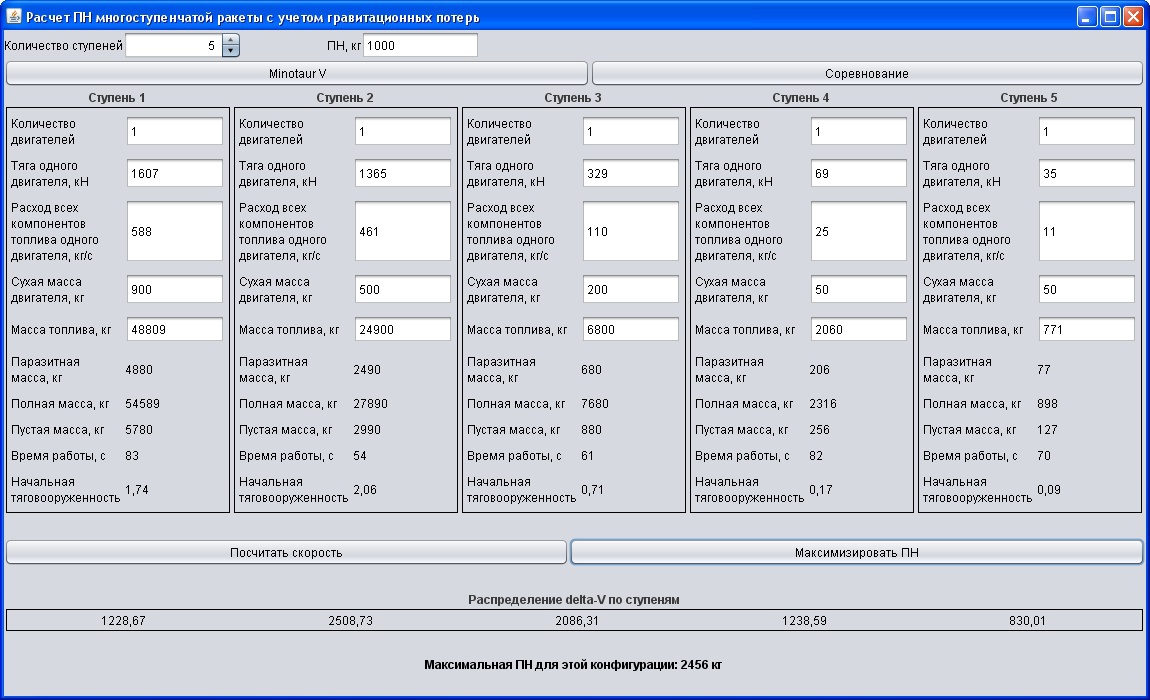
The main and only window of the program:

')
You can calculate the final speed of the rocket for the specified MON, by filling in the text fields of the parameters, by entering the MON from above and pressing the “Calculate Speed” button.
You can also calculate the maximum payload for these rocket parameters, in this case the “PN” field is not taken into account.
There is a real rocket with five steps “Minotaur V”. The “Minotaur V” button loads parameters similar to this rocket in order to show an example of how the program works.
In essence, this is a sandbox mode in which you can create rockets with arbitrary parameters, studying how different parameters affect the payload capacity of a rocket.

Competition

The "Competition" mode is activated by pressing the "Competition" button. In this mode, the number of controlled parameters is strongly limited for the same conditions of competition. At all steps are the same type of engines (this is necessary for clarity, the need for several steps). You can control the number of engines. You can also control the fuel distribution in stages and the number of stages. Maximum fuel weight - 300 tons. Pour less fuel possible.
Task : using the minimum number of engines to achieve maximum MON. If there are a lot of people willing to play, then each number of engines will have its own offset.
Those who wish can leave their result with the parameters used in the comments. Successes!

UPD: Thank you 0serg , improved formulas.