The logic of thinking. Part 12. Traces of memory

This series of articles describes a wave model of the brain that is seriously different from traditional models. I strongly recommend that those who have just joined begin reading from the first part .

The engram is the change that occurs to the brain at the time of memorization. In other words, an engram is a memory trace. It is quite natural that the understanding of the nature of engrams is perceived by all researchers as a key task in the study of the nature of thinking.
')
What is the difficulty of this task? If you take a regular book or an external computer drive, you can call both that and that. Both store information. But it is not enough to keep. To make information useful, you need to be able to read it and know how to operate it. And here it turns out that the form of information storage itself is closely connected with the principles of its processing. One thing determines the other.

Human memory is not just the ability to store a large variety of different images, but also a tool that allows you to quickly find and reproduce the relevant memory. At the same time, in addition to associative access to arbitrary fragments of our memory, we are able to link memories into chronological chains, reproducing not a single image, but a sequence of events.

Wilder Graves Penfield received well-deserved recognition for his contribution to the study of the functions of the cortex. Being engaged in the treatment of epilepsy, he developed a technique for open brain operations, in the course of which electrical stimulation was used, allowing to specify the epileptic focus. Exciting various parts of the brain with an electrode, Penfield recorded the reaction of conscious patients. This provided a detailed understanding of the functional organization of the cerebral cortex (Penfield, 1950). Stimulation of some areas, mainly the temporal lobes, caused vivid memories in patients, in which past events surfaced in the smallest detail. And the re-stimulation of the same places caused the same memories.

The clear localization in the cortex of many functions revealed by Panfil has set up searches for the same clearly localized traces of memory. In addition, the emergence of computers and, accordingly, ideas about how physical storage media of computer information is organized, stimulated the search for something similar in brain structures.

In 1969, Jerry Letvin said: “If a person’s brain consists of specialized neurons, and they encode the unique properties of various objects, then, in principle, there must be a neuron somewhere in the brain, through which we recognize and remember our grandmother.” The wording “grandmother's neuron” is fixed and often comes up when the conversation about the memory device comes. Moreover, there were direct experimental evidence. Neurons have been detected that respond to certain images, for example, clearly recognizing a particular person or a specific phenomenon. True, in more detailed studies, it turned out that the detected “specialized” neurons respond not only to one thing, but to groups in some sense of closely related images. So, it turned out that the neuron that reacted to Jennifer Aniston, also reacted to Lisa Kudrow, who starred along with Aniston in the television series Friends, and the neuron that recognized Luke Skywalker was also recognized by master Yoda (RK Kviroga, K. Koch, I. Fried, 2013).

In the first half of the twentieth century, Karl Lashley set very interesting experiments on memory localization. First, he trained the rats to find a way out in the maze, and then he removed various parts of the brain with them and again launched into the maze. So he tried to find the part of the brain that is responsible for the memory of the acquired skill. But it turned out that the memory was always preserved in one way or another, despite occasionally significant motility disorders. These experiments inspired Carl Pribram to formulate the theory of holographic memory that has become widely known and popular (Pribram, 1971).

The principles of holography, as well as the term itself, were invented in 1947 by Denech Gabor, who won the Nobel Prize in Physics for 1971 for this. The essence of holography is as follows. If we have a light source with a stable frequency, then dividing it by means of a translucent mirror into two, we will get two coherent light fluxes. One stream can be directed to the object, and the second to the photographic plate.


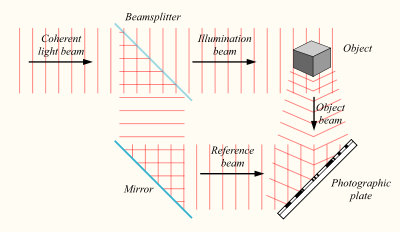
Create a hologram

As a result, when the light reflected from the object reaches the photographic plate, it will create an interference pattern with the stream illuminating the plate.

The interference pattern, imprinted on the photographic plate, will save information not only about the amplitude, but also about the phase characteristics of the light field reflected by the object. Now, if we illuminate a previously exposed plate, the original luminous flux will be restored, and we will see the memorized object in all its volume.


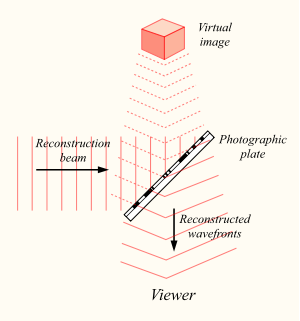
Hologram reproduction

The hologram has several amazing properties. First, the luminous flux saves volume, that is, looking at a phantom object from different angles, you can see it from different sides. Secondly, each area of ​​the hologram contains information about the entire light field. So, if we cut the hologram in half, first we will see only half of the object. But if we tilt our head, then beyond the edge of the remaining hologram we will be able to see the second “trimmed” part. Yes, the smaller the hologram fragment, the lower its resolution. But even through a small area you can, like through a keyhole, view the entire image. It is interesting that if there is a magnifying glass on the hologram, then through it it will be possible to examine with magnification other objects captured there.

As applied to memory, Pribram formulated: “The essence of the holographic concept is that images are restored when their representations in the form of systems with distributed information are properly brought into an active state” (Pribram, 1971).

The mention of the holographic properties of memory can be found in two contexts. On the one hand, calling the memory holographic, emphasize its distributed nature and the ability to restore images, using only part of the neurons, just as it happens with fragments of a hologram. On the other hand, it is assumed that a memory possessing hologram-like properties is based on the same physical principles. The latter means that since holography is based on the fixation of the interference pattern of light fluxes, memory, apparently, somehow uses the interference pattern resulting from the pulse coding of information. Brain rhythms are well known, and where there are fluctuations and there are waves, and, therefore, their interference is inevitable. So, the physical analogy looks quite appropriate and attractive.

But the interference of a thing is subtle, small changes in the frequency or phase of the signals should completely change its picture. However, the brain successfully works with a significant variation of its rhythms. In addition, attempts to impede the distribution of electrical activity by dissecting its sections and placing mica at the incision sites, overlaying strips of gold foil to create a circuit, creating epileptic foci by injecting aluminum paste do not disturb pathologically too brain activity (Pribram, 1971).

Speaking of memory, it is impossible to ignore the known facts about the relationship of memory and the hippocampus. In 1953, the patient, who is called HM ( Henry Molaison ), the surgeon removed the hippocampus (W. Scoviille, B. Milner, 1957). It was a risky attempt to cure severe epilepsy. It was known that removing the hippocampus of one of the hemispheres really helps with this disease. Given the exceptional power of epilepsy in HM, the doctor removed the hippocampus on both sides. As a result, HM's ability to memorize something completely disappeared. He remembered what was with him before the operation, but everything new flew out of his head as soon as his attention shifted.


Henry molaison

HM has long been investigated. In the course of these studies, countless different experiments were carried out. One of them turned out to be particularly interesting. The patient was offered to circle the five-pointed star, looking at it in the mirror. This is not a very simple task, causing difficulty in the absence of proper skill. The task was given by HM repeatedly and each time he perceived it as what he had seen for the first time. But it is interesting that with each time the task was given to him easier and easier. With repeated experiments, he himself noted that he expected this to be much more difficult.


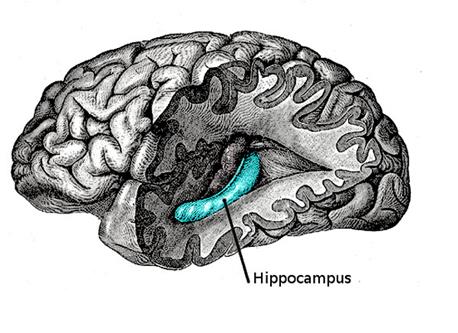
Hippocampus of one of the hemispheres

In addition, it turned out that a certain memory for events was still inherent in HM. For example, he knew about Kennedy's murder, although it happened after the removal of his hippocampus.

From these facts it was concluded that there are at least two different types of memory. One type is responsible for fixing specific memories, and the other is responsible for gaining some generalized experience, which is expressed in the knowledge of common facts or the acquisition of certain skills.

The case of HM is quite unique. In other situations involving the removal of the hippocampus, where there was no such complete bilateral damage as in HM, memory impairment was either not so pronounced or was absent altogether (W. Scoviille, B. Milner, 1957).

Now let's try to compare everything described with our model. We have shown that persistent repetitive phenomena form patterns of neuron detectors. These patterns are able to recognize the characteristic combination of features, and add new identifiers to the wave pattern. We have shown how the reverse reproduction of features by the concept identifier can occur. This can be compared with the memory of a generalized experience.

But such a generalized memory does not allow to recreate specific events. If the same phenomenon is repeated in different situations, we in our neural network simply receive associative links between the concept corresponding to the phenomenon and the concepts describing these circumstances. Using this associativity, you can create an abstract description consisting of concepts that occur together. The task of event memory is not to reproduce a certain abstract picture, but to recreate a previously memorized situation describing a specific event with all its unique unique features.

The difficulty is in the fact that in our model there is nowhere such a place where a complete and exhaustive description of what is happening would be localized. A full description is made up of many descriptions that are active in separate zones of the cortex. Each of the zones has a wave description in terms that are specific to this particular area of ​​the brain. And even if we somehow remember what happens on each of the zones separately, these descriptions will still need to be linked to each other in such a way as to create a complete image.

A similar situation occurs when we have a topographic projection and neurons with local receptive fields. Suppose that we have a neural network consisting of two flat layers (figure below). Suppose that the state of the neurons of the first layer forms a certain picture. This picture is transmitted through the projection fibers to the second layer. The neurons of the second layer have synaptic connections with those fibers that fall within the boundaries of their receptive fields. Thus, each of the neurons of the second layer sees only a small fragment of the original image of the first layer.


Topographic projection of the image on local receptive fields

There is an obvious way how to memorize the supplied picture on the second layer. It is necessary to choose a set of neurons so that their receptive fields completely cover the projected image. Remember on each of the neurons its own fragment of the image. And in order for a memory to become connected, mark all these neurons with a common marker indicating that they belong to the same set.

Such memorization is very simple, but extremely wasteful by the number of neurons involved. Each new picture will require a new distributed set of memory elements.

You can save money, if it turns out that different images repeat any common fragments, then you can not force a new neuron to memorize such a fragment, but to use an existing neuron, simply adding one more marker to it, now from the new image.

Thus, we come to the basic idea of ​​distributed memorization. We first describe it for a picture and a topographic projection.

We will apply various images to the first zone and project them onto the second zone. If we make the receptive fields of neurons small enough, then the number of unique images in each local area will not be so large. We can choose the size of the receptive field so that in the region, the dimensions of which will approximately coincide with the size of the receptive field of neurons, fit all the unique variants of local images.

Create spatial regions containing neuron detectors. Let us make sure that each area contains detectors of all possible unique images and that such areas cover the entire space of the second zone. To do this, we can use the principles of selection of factor sets described earlier.

The task of the detectors is to compare the images supplied to their receptive fields with the images characteristic of them. For such a comparison of images, you can use convolution on the receptive field R :



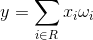
The response of the neuron will be the higher, the more the new image covers the image remembered. If we are interested not in the degree of coverage, but in the level of coincidence of images, then we can use the correlation of images, which is nothing more than a normalized convolution:



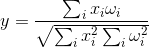
By the way, the same value is the cosine of the angle formed by the image vector and the weight vector:



As a result, in each local group of detectors, when applying a new picture, the neuron detectors that most accurately describe their local fragment will be triggered.

Now we will do the following: we will generate our unique identifier for each new image and mark the active neurons-detectors with it. We obtain that each image feed is accompanied by the appearance of a picture of activity on the second zone of the cortex, which is a description of this image through the signs available to the second zone. Creating a unique identifier and marking its active neuron detectors is the memorization of a specific event.

If we select one of the markers, find the neurons-detectors containing it, and restore the local images that are typical for them, we will get the restoration of the original image.

In order to memorize and reproduce many different images, the neuron detectors must have constant synaptic weights and have the ability to store as many markers as they need to remember.

Let us show the work of distributed memorization using a simple example. Assume that we generate contour images of various geometric shapes on the upper zone (figure below).


Image feed

We will train the lower zone on the selection of various factors using the de-correlation method. The main images that will appear in each small receptive field are lines from different angles. There will be other images, such as intersections and angles, characteristic of geometric shapes. But the lines will dominate, that is, meet more often. This means that they will stand out primarily as factors. The real result of such training is shown in the figure below.


Fragment of a field of factors extracted from contour images

It can be seen that many vertical and horizontal lines stand out, differing in their position on the receptive field. This is not surprising, since even a small offset creates a new factor that does not have intersections with its parallel "twins." Suppose that we somehow complicated our network in such a way that the adjacent parallel “twins” merged into one factor. Further, let us assume that in small areas factors have emerged, as shown in the figure below, with a certain discreteness describing all possible directions.


Factors in a small area that correspond to different directions with a one-hour resolution

Then the result of learning the entire area of ​​the cortex can be roughly depicted as follows:


The conditional result of learning the zone of the cortex. For clarity, the neurons are not placed on a regular grid.

Now we will give a square image on the trained bark zone. Neurons that see a characteristic stimulus on their receptive field are activated (figure below).


Reaction of a trained bark zone to an image of a square

Now we will generate a random unique number - the identifier of the memory. For simplicity, we will not use our wave networks for the time being; we will restrict ourselves to the assumption that each neuron can also store a set of identifiers, in addition to synaptic weights, that is, a certain large array of unordered numbers. Make all active neurons memorize the newly generated identifier in their sets. Actually, this action we will fix the memory of what he saw square.

By submitting new images, for each of them we will generate our unique identifier and add it to the neurons that have responded to the current image. , - , , , , , . , , . , , , , ( ).


, «»

, .

-, , . . , . « », , - . , , .

, , . -, , , , .

– . , , , .

-, , . , , . . , -, .

, , . .

. - , , , .

, . , - . , , , , .

, . – -, , .

, . , . , - , , . , . , . , , , , , . . , , « ».

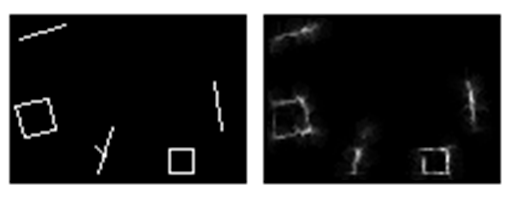
HM , , , . , , . - , .

, . – -. , , , , - . . , . – , , . – , , . . , - , , .

, . - , , , , , . , , . , . , , , .

References

Continuation

Previous parts:
Part 1. Neuron
Part 2. Factors
Part 3. Perceptron, convolutional networks
Part 4. Background Activity
Part 5. Waves of the brain
Part 6. The system of projections
Part 7. Human-computer interface
Part 8. Selection of factors in the wave networks
Part 9. Patterns of neuron detectors. Reverse projection
Part 10. Spatial self-organization
Part 11. Dynamic neural networks. Associativity