Optimization of the geometric algorithm of learning ANN in the analysis of independent components
Good afternoon, dear habrovchane. Perhaps many of you will ask yourself the question: “Where is the description of the main algorithm?”.
So, below will be links to sources, and I will not rewrite the main algorithm.
Immediately explain. This article is the result of my research work, and later on the subject of my diploma.
But enough of the opening words. Go!
ANNs are an attempt to use the processes occurring in the nervous systems of living beings to create new information technologies.
The main element of the nervous system is the nerve cell, abbreviated as neuron. Like any other cell, the neuron has a body called soma, inside which is located the nucleus, and numerous processes go out - thin, densely branching dendrites, and a thicker axon splitting at the end (Fig. 1).

Fig.1. Simplified Biological Nerve Cell Structure
')
Input signals enter the cell through synapses, the output signal is transmitted by the axon through its nerve endings (collateral) to the synapses of other neurons, which can be located both on the dendrites and directly on the cell body.
We will consider it as the main used model of a multilayer NS direct propagation. A multilayer network consists of neurons located at different levels, when, in addition to the input and output layers, there is still at least one intermediate (hidden) layer. The generalized structure of a two-layer NA is shown in (Fig. 2).

Fig. 2. The generalized structure of the two-layer NA (with one hidden layer)
The output of the i-th neuron of the hidden layer can be written as
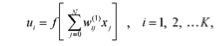
and output signals
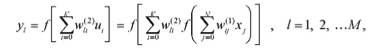
To select the signals of the S (t) sources contained in the mixture of signals, we use the structure of the adaptive filter based on a single-layer INS (Fig. 3) proposed in the 80s by Herolt and Jutten, where X is the matrix of vectors of the observed signals, formed in accordance with the equation ( 1) using an unknown mixing matrix A, W is the weights matrix of the neural network.
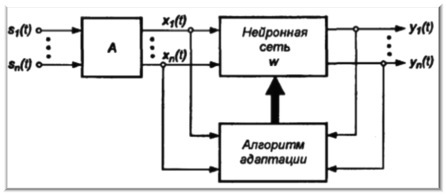
Fig. 3. The block diagram of the adaptive filter on the INS
So, as you know, any neural network requires training.
There are various learning algorithms, with a teacher, without a teacher, combined.
In this paper, a rather unusual learning algorithm of the INS was considered - geometric.
First, consider its main differences:
The following situation was investigated in the work.
A mixture of various signals is input (I emphasize in advance that the number of signals is already known).
It was necessary to develop such an algorithm for training the neural network, which would allow the separation of signals from the mixture with maximum accuracy.
Figure 4a shows the source signals. It is noticeable that 2 independent components are clearly distinguished, each of which describes a signal.
Figure 4b shows a mixture of signals. The signals correlate with each other, and it becomes quite difficult to distinguish them (try to superimpose one image on another).

Fig.4. Geometric interpretation of multiplication by matrix A
(a) - signals of sources, b) - signals of mixtures)
From (1) it is clear that the mixture of signals is obtained as a result of multiplying the signals of the sources by the mixing matrix A:
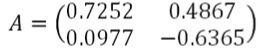 ,
,
which in turn is represented as a rotation matrix:
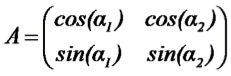 .
.
From this rather simple idea was born the geometrical algorithm of ANN learning - histGEO.
The task of the restoration of the mixing matrix is to find
angles α1 and α2 of the rotation matrix. In general, the number of angles is equal to the number of independent components,
involved in mixing.
Briefly histGEO operation scheme for processing
super-Gaussian signals can be described as follows:
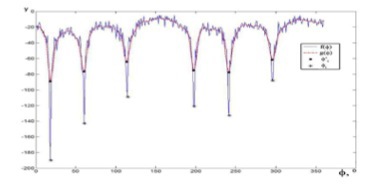
Fig.5. Search for angles φ i using gradient descent.
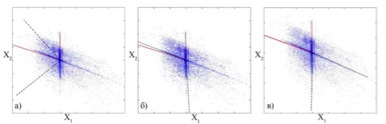
Fig.6.1. The results of the evaluation of the mixing matrix for 2 audio signals
(a - geoica, b -fastgeo, c - histgeo)
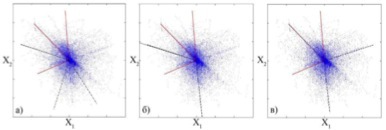
Fig. 6.2. The results of the evaluation of the mixing matrix for 3 audio signals.
Case of overflow base
(a - geoica, b - fastgeo, c - histgeo)
Practical studies of the considered algorithms were carried out in the system
Matlab 7.5 Mathematical Modeling Using Extension Packages
fastICA, geoICA, ICALab (extensions for learning.
The work was divided into two parts with increasing difficulty of separation:

Fig.7.1. Characteristics of the source signals: the shape of the source signals
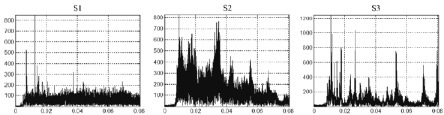
Fig.7.2. Characteristics of the original signals: frequency spectra

Fig.7.3. Characteristics of the original signals: probability distributions
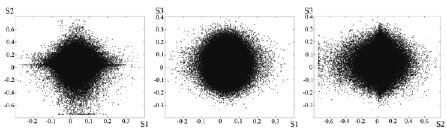
Fig.7.4. Source Signal Characteristics: Scatterplots
In addition to the often-occurring super-Gaussian distribution (audio signals, images, video, etc.),
there are so-called sub-Gaussian signals (various kinds of noise, statistical values, competition of individuals of the same species in nature).
And it is sometimes difficult to separate signals of this type, because they are implicitly presented and greatly complicate the distribution pattern.
Oddly enough, rather simple geometric algorithms were able to solve this problem.
It is enough just to choose the geometric feature that characterizes an independent component.
The signals on the output of the INS will be
those. the problem of linear filtering is reduced to finding the correct values of the coefficients
weights matrix of W.
From the comparison of the scatterplots of the initial sources and the obtained mixtures X
(Fig. 8) it can be concluded that multiplication by the mixing matrix A is equivalent to
rotation of the independent components at some angles α1 and α2 in the x1Ox2 plane.
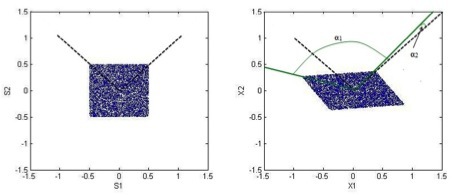
Fig.8. Geometric interpretation of the multiplication by the mixing matrix A
(a - signals of sources, b - signals of mixtures)
To convert data into a convenient form for work, it was necessary
to carry out the procedure for the decorrelation of a set of signals ("bleaching"),
which translates their joint correlation matrix into
diagonal form whose elements are the variances of these
signals (Fig.9). And the required geometric sign turned out to be the diagonal of the square:
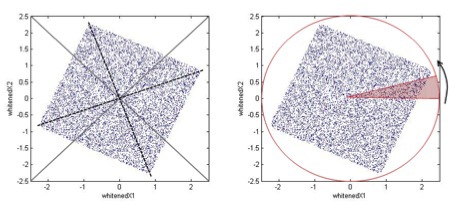
Fig.9. Decreted ("bleached") signals X1 and X2.
(a - search for a suitable geometric feature, b - building a distribution histogram)
From the conditions of hitting the points in the sector of the circle - obviously more
on the area, than the area of the analyzed distribution (fig.9b) -
the density distribution of points in the sector was calculated as
the function of the angle φ (Fig.10):
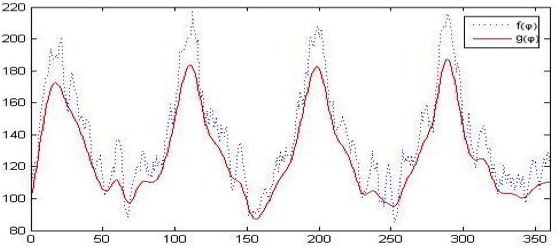
Fig.10. Search for angles φ i in the histgeo algorithm
where f * (φ) - f (φ), “smoothed” with a filter.
To reduce the error, an array of deviation values of all 4 diagonals relative to the original diagonals, respectively (45 o , 135 o , 225 o , 315 o ) was formed (fig.11), then the average deviation was found.
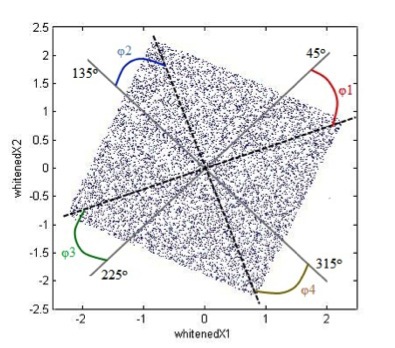
Fig.11. Search for angles of deviation of diagonals from given angles.
Knowing the angle at which the diagonals are rotated, as well as the fact that the diagonals in the center of the square intersect, it is possible to rotate all points relative to this center by this angle in the direction of the corresponding diagonals. To do this, it is necessary to calculate the restoring matrix:
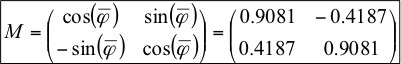
The resulting distribution graphically coincides with the initial one, which
clearly shown in Figure 12:
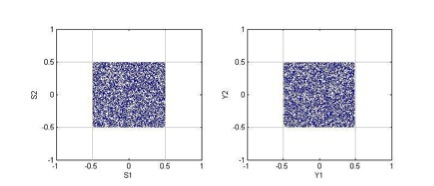
Fig.12. Comparison of the reference distribution S (a) and the recovered Y (b).
To find the mixing matrix A ', you must use
the reverse of the decorellation procedure. The resulting matrix
has the form:
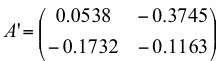
The error of the mutual influence of the matrices A and A ':
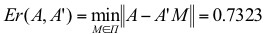
Table 1. The values of coefficients of kurtosis for matrices S, X, Y:
Coefficient of kurtosis:
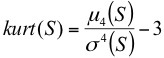
At this stage, it cannot be said that the algorithm is universal and applicable in the case of non-square mixing matrices for any class of distributions, but it can be noted with confidence that in the case of square matrices this algorithm does its job.
Bibliography:
So, below will be links to sources, and I will not rewrite the main algorithm.
Immediately explain. This article is the result of my research work, and later on the subject of my diploma.
But enough of the opening words. Go!
1. Artificial neural networks
ANNs are an attempt to use the processes occurring in the nervous systems of living beings to create new information technologies.
The main element of the nervous system is the nerve cell, abbreviated as neuron. Like any other cell, the neuron has a body called soma, inside which is located the nucleus, and numerous processes go out - thin, densely branching dendrites, and a thicker axon splitting at the end (Fig. 1).

Fig.1. Simplified Biological Nerve Cell Structure
')
Input signals enter the cell through synapses, the output signal is transmitted by the axon through its nerve endings (collateral) to the synapses of other neurons, which can be located both on the dendrites and directly on the cell body.
2. Multilayer perceptron
We will consider it as the main used model of a multilayer NS direct propagation. A multilayer network consists of neurons located at different levels, when, in addition to the input and output layers, there is still at least one intermediate (hidden) layer. The generalized structure of a two-layer NA is shown in (Fig. 2).

Fig. 2. The generalized structure of the two-layer NA (with one hidden layer)
The output of the i-th neuron of the hidden layer can be written as
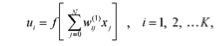
and output signals
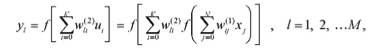
To select the signals of the S (t) sources contained in the mixture of signals, we use the structure of the adaptive filter based on a single-layer INS (Fig. 3) proposed in the 80s by Herolt and Jutten, where X is the matrix of vectors of the observed signals, formed in accordance with the equation ( 1) using an unknown mixing matrix A, W is the weights matrix of the neural network.
X = AS (1)
Fig. 3. The block diagram of the adaptive filter on the INS
3. The use of geometric algorithms for teaching the ins
So, as you know, any neural network requires training.
There are various learning algorithms, with a teacher, without a teacher, combined.
In this paper, a rather unusual learning algorithm of the INS was considered - geometric.
First, consider its main differences:
- Intuitive clarity and visibility
- High processing speed
- Ability to use for non-square mixing matrices (only in case of super-Gaussian distributions)
- Easy programming
The following situation was investigated in the work.
A mixture of various signals is input (I emphasize in advance that the number of signals is already known).
It was necessary to develop such an algorithm for training the neural network, which would allow the separation of signals from the mixture with maximum accuracy.
Figure 4a shows the source signals. It is noticeable that 2 independent components are clearly distinguished, each of which describes a signal.
Figure 4b shows a mixture of signals. The signals correlate with each other, and it becomes quite difficult to distinguish them (try to superimpose one image on another).

Fig.4. Geometric interpretation of multiplication by matrix A
(a) - signals of sources, b) - signals of mixtures)
From (1) it is clear that the mixture of signals is obtained as a result of multiplying the signals of the sources by the mixing matrix A:
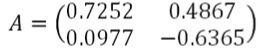 ,
,which in turn is represented as a rotation matrix:
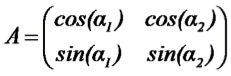 .
.From this rather simple idea was born the geometrical algorithm of ANN learning - histGEO.
4. Algorithm histGEO for the case of super-Gaussian distributions.
The task of the restoration of the mixing matrix is to find
angles α1 and α2 of the rotation matrix. In general, the number of angles is equal to the number of independent components,
involved in mixing.
Briefly histGEO operation scheme for processing
super-Gaussian signals can be described as follows:
- build the scatter diagram of the component of the matrix X;
- the probability density distribution is calculated as a function of the angle φ: f = f (φ);
- the obtained distribution is processed using an averaging software filter to smooth the surface of the obtained function, while preserving the location of the extremes;
- the locations of the possible localization of the minima of the function g = -f (φ), where f (φ) is “smoothed” g (φ)), are roughly determined;
- using the gradient descent algorithm, the coordinates of the angles φ i are refined (Fig.5.)

Fig.5. Search for angles φ i using gradient descent.
- the coefficients of the restoring matrix M are calculated
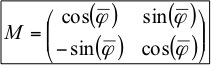
where n is the number of independent components in the mixture; - at the stage of testing the algorithm, the obtained values of the angles φ; are plotted on a scatterplot and compared with α (fig. 6.1-6.2)

Fig.6.1. The results of the evaluation of the mixing matrix for 2 audio signals
(a - geoica, b -fastgeo, c - histgeo)

Fig. 6.2. The results of the evaluation of the mixing matrix for 3 audio signals.
Case of overflow base
(a - geoica, b - fastgeo, c - histgeo)
Audio processing
Practical studies of the considered algorithms were carried out in the system
Matlab 7.5 Mathematical Modeling Using Extension Packages
fastICA, geoICA, ICALab (extensions for learning.
The work was divided into two parts with increasing difficulty of separation:
- Evaluation of the mixing matrix in the problem with a square matrix, the signals of the sources S - speech, noise, music (Fig.7.1-7.4)
- Evaluation of the mixing matrix in a problem with an overcrowded basis, signals from sources S - speech, noise, music

Fig.7.1. Characteristics of the source signals: the shape of the source signals

Fig.7.2. Characteristics of the original signals: frequency spectra

Fig.7.3. Characteristics of the original signals: probability distributions

Fig.7.4. Source Signal Characteristics: Scatterplots
5. The algorithm histGEO for the case of sub-Gaussian distributions.
In addition to the often-occurring super-Gaussian distribution (audio signals, images, video, etc.),
there are so-called sub-Gaussian signals (various kinds of noise, statistical values, competition of individuals of the same species in nature).
And it is sometimes difficult to separate signals of this type, because they are implicitly presented and greatly complicate the distribution pattern.
Oddly enough, rather simple geometric algorithms were able to solve this problem.
It is enough just to choose the geometric feature that characterizes an independent component.
The signals on the output of the INS will be
Y=WX (2)those. the problem of linear filtering is reduced to finding the correct values of the coefficients
weights matrix of W.
From the comparison of the scatterplots of the initial sources and the obtained mixtures X
(Fig. 8) it can be concluded that multiplication by the mixing matrix A is equivalent to
rotation of the independent components at some angles α1 and α2 in the x1Ox2 plane.

Fig.8. Geometric interpretation of the multiplication by the mixing matrix A
(a - signals of sources, b - signals of mixtures)
To convert data into a convenient form for work, it was necessary
to carry out the procedure for the decorrelation of a set of signals ("bleaching"),
which translates their joint correlation matrix into
diagonal form whose elements are the variances of these
signals (Fig.9). And the required geometric sign turned out to be the diagonal of the square:

Fig.9. Decreted ("bleached") signals X1 and X2.
(a - search for a suitable geometric feature, b - building a distribution histogram)
From the conditions of hitting the points in the sector of the circle - obviously more
on the area, than the area of the analyzed distribution (fig.9b) -
the density distribution of points in the sector was calculated as
the function of the angle φ (Fig.10):

Fig.10. Search for angles φ i in the histgeo algorithm
f=f(φ)g(φ)=f*(φ) ,where f * (φ) - f (φ), “smoothed” with a filter.
To reduce the error, an array of deviation values of all 4 diagonals relative to the original diagonals, respectively (45 o , 135 o , 225 o , 315 o ) was formed (fig.11), then the average deviation was found.

Fig.11. Search for angles of deviation of diagonals from given angles.
Knowing the angle at which the diagonals are rotated, as well as the fact that the diagonals in the center of the square intersect, it is possible to rotate all points relative to this center by this angle in the direction of the corresponding diagonals. To do this, it is necessary to calculate the restoring matrix:
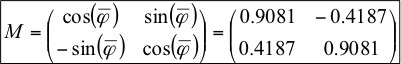
The resulting distribution graphically coincides with the initial one, which
clearly shown in Figure 12:

Fig.12. Comparison of the reference distribution S (a) and the recovered Y (b).
To find the mixing matrix A ', you must use
the reverse of the decorellation procedure. The resulting matrix
has the form:
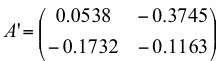
The error of the mutual influence of the matrices A and A ':
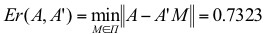
Table 1. The values of coefficients of kurtosis for matrices S, X, Y:
| S | X | Y | |
| kurt1 | -0.8365 | -0.7582 | -0.8379 |
| kurt2 | -0.8429 | -0.8341 | -0.8465 |
Coefficient of kurtosis:
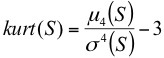
6. Conclusions
- The possibility of applying the geometGE algorithm GEGEO to the class of sub-Gaussian distributions has been verified.
- Despite its apparent simplicity, geometric algorithms are an effective ANN learning mechanism in adaptive filtering problems.
- The developed optimized variant of the histGEO algorithm is applicable to signals of both super-Gaussian and sub-Gaussian type.
- With an increase in the number of sources in the mixture, it becomes more difficult to make a correct estimate of the matrix, since the extremes of the function g (φ) become less pronounced and it is possible that the solution falls into one of the local minima.
- The effectiveness of the algorithm in the case of separation of signals with an overcrowded basis (variants of a non-square mixing matrix) requires additional studies.
At this stage, it cannot be said that the algorithm is universal and applicable in the case of non-square mixing matrices for any class of distributions, but it can be noted with confidence that in the case of square matrices this algorithm does its job.
Bibliography:
- Khaikin S. Neural networks: a full course / S. Khaikin. - M .: Publishing House "Williams", 2006. - 1104 p.
- Bormontov E.N., Klyukin V.I., Tyurikov D.A. Geometric learning algorithms in the problem of analyzing independent components / E.N. Bormontov, V.I. Klyukin, D.A. Tyurikov - VSTU Bulletin, v.6, №7. - Voronezh: VSTU, 2010.
- A. Jung, FJ Theis, CG Puntonet EW Lang. Fastgeo is a histogram based approach to linear ICA. Proc. of ICA 2001, pp. 418-423, 2001.
- FJ Theis. A geometric algorithm for overcomplete linear ICA. B. Ganslmeier, J. Keller, KF Renk, Workshop Report of the Graduiertenkolleg, pages 67-76, Windberg, Germany, 2001.
- G. F. Malykhina, A. V. Merkusheva Robust methods for separating a mixture of signals and analyzing independent components with noisy data / G. F. Malykhina, A. V. Merkusheva SCIENTIFIC INSTRUMENTATION, 2011, vol. 21, no. 1, p. 114-127
- XIX International Scientific and Technical Conference "Radiolocation, Navigation, Communication" (RLNC-2013) Section 1. Optimization of the geometric algorithm for teaching the INS when analyzing independent components. E.N. Bormontov, V.I. Klyukin, D.A. Tyurikov - 2013
Source: https://habr.com/ru/post/216225/
All Articles