RASW: Improving Viola-Jones Method

From the translator:

Good day!
Recently, I was looking for ways to increase the speed of the Viola-Jones detector and came across an interesting 2013 article “RASW: a Run-time Adaptive Sliding Windowto Improve Viola-Jones Object Detection”. It presents an effective approach to improving the performance of detectors based on the principle of the scanning window and cascade classifiers. I did not find a description of this approach in Russian and decided to fill this gap. In this translation, I omitted the description of the Viola-Jones algorithm, since much has already been said about it, including on the habrahabr.ru/post/133826 .

RASW: A Run-time Adaptive Sliding Windowto Improve Viola-Jones Object Detection

Francesco Comaschi, Sander Stuijk, Twan Basten and Henk Corporaal
Electronic Systems Group, Eindhoven University of Technology, The Netherlands
ff.comaschi, s.stuijk, aabasten, h.corporaalg@tue.nl

annotation

Among the algorithms for detecting objects in images, the Viola-Jones method, implemented in the OpenCV library, has become the most popular. However, as with other detectors based on the scanning window principle, the amount of computation required increases with the size of the image being processed, which is not good with real-time image processing. In this article, we propose an effective approach — changing the step size of a scanning window during processing — to increase speed without loss of accuracy. We also demonstrate the effectiveness of the proposed approach on the Viola-Jones method. When compared with the implementation of the detector in the OpenCV library, we obtained a speed increase (frames per second) up to 2.03 times without loss in accuracy.
')

Introduction

Innovations in the field of semiconductor technology and computer architectures make real-life new scenarios for the use of computer vision, in which the ability to analyze the situation in real time is crucial. A good example of a real-time task that finds application in many areas is the detection of an object in an image. Such an object is often the face of a person [1]. At the moment there is a huge variety of approaches for the detection of individuals. The method proposed by Viola and Jones [2] in 2001 was a real breakthrough in this area. This method has gained great popularity due to its high accuracy and serious theoretical basis. However, the complexity of computations still makes this method a rather serious task to satisfy real-time requirements (for example, bandwidth) even on powerful platforms. The speed of scanning images strongly depends on the step size of the scanning window Δ — the number of pixels by which the scanning window is shifted. In most of the available implementations, the step is constant and is determined at the compilation stage, which means that the window is shifted by a constant value and does not depend on the content of the image. In this article, we offer the Run-time Adaptive Sliding Window (RASW), which improves throughput without compromising the accuracy of the algorithm by changing the scanning step at run time.

Review of existing solutions

In recent years, several hardware implementations of the Viola-Jones face detector with a high bandwidth [3] - [5] have been proposed. However, such solutions have two major drawbacks:
1) they require significant engineering effort, which implies high one-time costs;
2) they are not flexible enough, which makes it impossible to adapt the system to any changes in the application scenario.

Another way to speed up the algorithm is to apply the implementation on the GPU [6] - [8]. However, the amount of energy consumed by the GPU makes this solution impractical for embedded systems. However, the implementation on the GPU can be used in conjunction with the optimization proposed in this article. In particular, parallelization can be used to calculate features and scan windows of different sizes. More about this is written in [6].

In [9], the authors propose a solution based on the implementation of OpenCV optimized for embedded systems, but the implementation itself remains unchanged. Our algorithmic optimization improves throughput by reducing the amount of computation required without degrading accuracy.

The first step in an object detection system is usually a scene scan in search of candidate image regions. This stage contains a large amount of computation. Lampert and others in work [10] offer an analytical approach, known as Efficient Subwindow Search, to provide object localization. However, the proposed approach relates specifically to the localization of the object, which means that the number of objects present in the image must be known in advance. Such an approach can be extremely effective in such a task as searching for an image on the Internet, but it is not clear from [10] what happens if there are several instances of the object of interest on the image. In addition, for the application of ESS, a restrictive function must be constructed in a certain way, and such a function for the cascade classifier was not presented in [10]. The approach presented in this article is intended for cascade classifiers, does not require additional information (such as a limiting function) and can be used for images with any number of objects.

In [11], the authors consider a method based on the visual search in humans model for the rapid detection of objects. Comparing their work with the Viola-Jones detector in OpenCV, they received an acceleration of an average of 2 times, due to a slight decrease in accuracy. The results of the work are presented only for one image, so it is difficult to judge whether the indicators will remain when testing for more images. In addition, the approach is proposed for use with images containing only one face and it is not clear how to apply this approach to images with several faces. While the results are given for different values ​​of the scaling factor, the effect of other parameters on image scanning has not been systematically studied. The results of our approach are presented for a standard database of individuals and the influence of various parameters has been carefully studied.

In [12], the authors propose an interesting method for reducing missed detections in a detector cascade with increasing sliding step of a scanning window. The authors presented promising results on several bases of individuals. However, the approach proposed in [12] requires training off-line decision tree for location evaluation. In addition, the use of points of interest adds an additional amount of computation, which makes it difficult to use in case of memory limitations. Algorithmic optimization presented in this article is based on information available at runtime; it does not require additional training and does not add significant calculations to the standard principle of the scanning window.

RASW

Usually, in implementations of the Viola-Jones method, with each change in the size of a scanning window (or image), this window moves through the image with a scanning step Δ. We will distinguish the step size along the x axis and y axis, i.e. Δ _X and Δ _Y, respectively. For simplicity, we leave the notation Δ, for cases when Δ _X = Δ _Y. Influence scanning step affects both detection accuracy and throughput. A higher value increases the throughput, but at the same time affects the quality of recognition, as some objects can be skipped. If for moving the scanning window we find such a criterion that the window moves faster in areas that do not contain objects, and more slowly in the immediate vicinity of the object, then we can increase the scanning speed of the entire image without degrading the quality. Moreover, moving the window faster in homogeneous areas of the image, we reduce the chance of the classifier to mistakenly find the object in the background image. In most existing implementations, the step size is a fixed value, and Δ = 1 or Δ = 2, because higher values ​​result in lower quality.

Our analysis revealed a relationship between the presence of a face in the image area and the classifier number in the cascade, on which this window is rejected (we will call this number the output level). In particular, in areas containing only background, the window is rejected at earlier stages of the cascade, and, in general, the closer the face, the higher the exit level.

Picture 1


Figure 1 contains a test image and for this image, the output step values ​​were recorded for each scanning window. If the upper left corner of the window has coordinates (x, y), then the pixel is displayed with a brightness inversely proportional to the output level. In other words, the higher the output level, the darker the pixels.

Our analysis shows that the window can be boldly shifted to a larger step with a low exit level, because in most cases this means that this area does not contain the desired objects. And when approaching the exit stage to the maximum value, it makes sense to reduce the scanning step so as not to miss the desired object. The main idea is to spend less time on the regions of the image, which with a high probability do not contain the desired objects. The proposed approach allows discarding hopeless regions using spatial data locality. Even if the dropped regions were not the most expensive in terms of calculations, a significant reduction in the number of windows leads to faster processing of each image, without affecting the quality. This is especially beneficial because with a direct drop of the window, it is possible to avoid the preliminary normalization of the image of the subwindow, which is a rather expensive operation. This normalization is necessary to minimize the influence of various lighting conditions in the Viola-Jones method [2], [9].

Figure 2


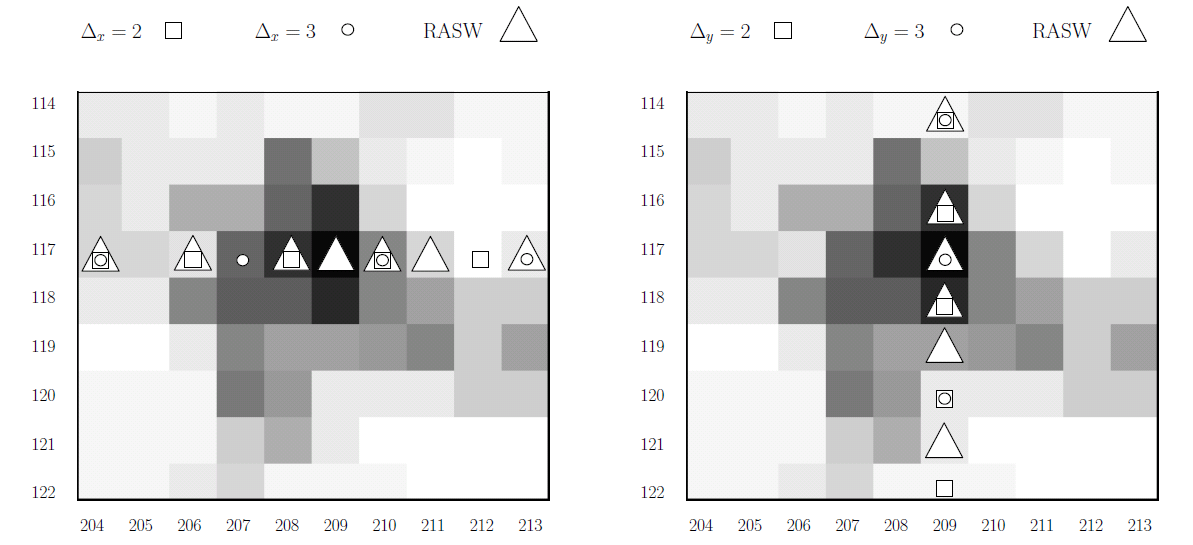
Figure 2 presents a graphical explanation of the benefits of the RASW approach. To make the drawing more readable, we will separate the directions along the x (left) and y (right) axes. Gray blocks are enlarged pixels from 204 to 213 (x axis) and from 114 to 122 (y axis) of the image shown in Fig. 3 (right). The black pixel in the position (209, 117) corresponds to the right lower face detected in Figure 1. For each of the approaches presented in Figure 4, the corresponding geometric shape is in the pixel where the scanning window is located. In Figure 2 (left), we see how, by taking a constant step Δ _X = 2 or Δ _X = 3, the detector is not able to place the scanning window in the place where the face is present. The RASW approach automatically reduces the step size ΔX when approaching a face, which allows the window to be properly positioned. The same behavior can be observed in fig. 4 (right), with the difference that in this case the constant step Δ _Y = 3 also allows the window to be positioned properly.

Algorithm 1


Algorithm 1 represents the RASW implementation. Each time the scanning window is moved, a cascade classifier is started for it, which returns the output stage (line 7). If the output level is n - the number of classifiers in the cascade - then the desired object is found (line 8) and the position, dimensions of the current window are placed in the vector V (line 10). The window pitch can take 3 different values: Δ _{x, max} , Δ _{x, min} and Δ _{x, nom} , depending on the output level of the previous window position (this is also true for the y direction). In order to assign the correct values ​​to ΔX and Δ _y , we must store information about the output level of the previous window position. This information can be stored directly in the variables Δ _X and Δ _y . In our implementation, the window moves from left to right, from top to bottom, so information relating to the x direction can be stored in the integer variable Δ _X. On the other hand, when the window reaches the end of the line, the step information along the y axis should be saved for the entire line, that is, Δ _y is an array of integers. At each iteration of the algorithm, Δ _X and Δ _y [x] decrease by one, and when both variables become zero, the current window is fed to the input of the classifier. If only one step value reaches this condition, then this variable is initialized with the minimum value (lines 20 and 22). The transition from one value of Δ to another (for both directions) is determined at the time of execution based on four threshold values: Δ _{x, t1} , Δ _{x, t2} , Δ _{y, t1} , Δ _{y, t2} . These parameters are set at compilation and they can take values ​​from 0 to n + 1, with Δ _{x, t1} <Δ _{x, t2} and Δ _{y, t1} <Δ _{y, t2} . We take into account the particular case when the step Δ _x is a constant and is Δ _{x, min} (Δ _{x, t1} = Δ _{x, t2} = 0), Δ _{x, nom} (Δ _{x, t1} = 0, Δ _{x, t2} = n + 1) or Δ _{x, max} Δ _{x, t1} = n + 1). the same is true for step Δ _y . For brevity, in lines 12-18 of Algorithm 1, we present only the code related to the x axis, but the similar code, with some changes, should be applied to the y axis. Different threshold values ​​provide different ratios throughput - accuracy. Other ratios also affect these ratios: the scaling factor s, the merge threshold γ. We chose the following values: Δ _{x, max} = 3, Δ _{x, nom} = 2, Δ _{x, min} = 1, because higher values ​​degrade the quality of the detector.

results

In this section, we demonstrate the effectiveness of our approach by comparing implementations with fixed and adaptive steps. The experiments were carried out on a quad-core Intel Core i7 with a clock frequency of 3.07 GHz. The CMU + MIT database was used [15].

The following implementations were considered: (I) static: Δ _X and Δ _{Y are} constant and equal to 1, 2 or 3 (a total of 9 combinations); (Ii) OpenCV 1: Δ _X = 2 for the entire image, if no face was detected at the previous step, otherwise Δ _X decreases to 1. Δ _Y remains constant and equal to 1; (III) OpenCV 2: Δ = 1, if the size of the current reduced image is less than 2 times smaller than the size of the original image, otherwise Δ = 2 otherwise. Both Δ _X and Δ _{Y change} .

Note that the first 2 approaches (static and OpenCV 1) used for our comparison are special cases of the proposed RASW approach. In particular, each combination of the static approach can be obtained from Algorithm 1 by assigning Δ _t2 and Δ_t1 to the corresponding values. The second approach (OpenCV 1) can be obtained by setting Δ _{x, t1} = 0, Δ _{x, t2} = n, Δ _{y, t1} = Δ _{y, t1} = 0.

To illustrate the benefits of RASW, we tested various approaches for several values ​​of the other two parameters: the scaling factor (s) and the merging threshold (γ). We selected the following parameters: s ∈ {1.1, 1.2, 1.3, 1.4, 1.5} and γ ∈ {1, 2, 3, 4, 5}. Larger values ​​of these parameters reduce accuracy. With five possible values ​​for x, five values ​​for γ eleven different approaches to choosing Δ (nine static combinations plus two OpenCV approaches), we end up with 275 different configurations for the chosen approaches. With regard to RASW, various options for the threshold parameters Δ _{x, t1} , Δ _{x, t2} , Δ _{y, t1} , Δ _{y, t2 are} possible. Since the number of steps of the selected classifier is n = 25, in order to perform thorough testing of our method within a reasonable time, we take the parameter values ​​in the range [0; n + 1]. In particular, Δ _{x, t1} , Δ _{x, t2} , Δ _{y, t1} , Δ _{y, t2} ∈ {0, 5, 10, 15, 20, 25, 26}, which leads to 28 possible combinations for each direction. Considering the possible values ​​of s and γ, we get a total of 19,600 configurations.

To analyze the performance of the proposed algorithm, we use two metrics that are often used when comparing object detection algorithms: recall (recall) and precision (precision). They are defined as follows:

;

where TP is the number of correctly defined objects, FN is the number of missing objects, FP is the number of false positives. Among all the created configurations, we show only the so-called Pareto points, which are local optimal solutions that fix all the optimal compromises in the project space [17] (In order for our results to conform to the traditional Pareto definition of the point [17], we use 1 - Recall instead of recall, 1 - precision instead of precision. Thus, theoretically, the best configuration coincides with the origin). The configuration prevails over the other configuration, if it is at least not worse in each of the indicators. We will consider only those configurations over which no other configuration prevails. A set of such configurations is Pareto minimal. All elements of this set are Pareto points.

Figure 3


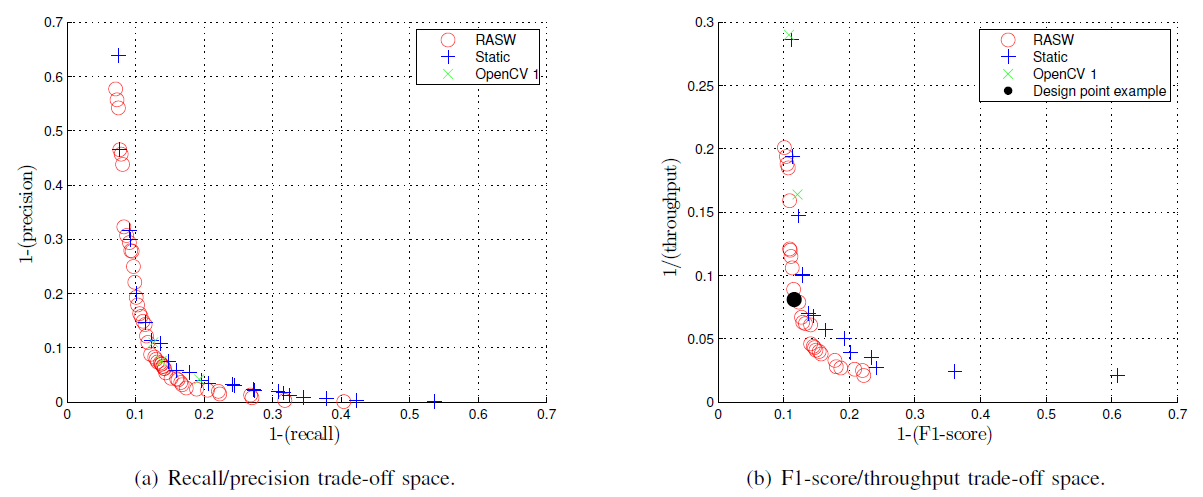
In fig. 3 (a) shows the Pareto points obtained for the basic (static, OpenCV 1, OpenCV 2) and RASW approaches in 2-dimensional call / accuracy space (recall / precision). The Pareto-minimal set of configurations of basic implementations contains 27 Pareto points, while the Pareto-minimal set of the RASW approach contains 48 Pareto points. In fig. 3 (a) we can see that for each Pareto-Minimal configuration of the basic approaches, one can find the RASW configuration with the same accuracy and the same (or best) recall.

For embedded systems, where images must be processed in real time, throughput is of prime importance - the number of frames processed per second (FPS). To visualize Pareto-minimal solutions when considering bandwidth, we will use the F1-score, a frequently used metric that combines accuracy and feedback [18]. An F1 score can be considered as a weighted average of feedback and accuracy, at best, a value of 1, and at worst - 0



and fig. 3 (b) presents the Pareto points obtained for the basic and RASW approaches in the 2-dimensional F1-score / throughput space (using 1 - F1-score and 1 / throughput throughput in order for the theoretically optimal solution to coincide with the beginning of the axes). The Pareto-minimal set of configurations of basic implementations contains 16 Pareto points while the RASW set is. From fig. 3 (b) we see that for a given accuracy, the RASW approach always provides at least one configuration that provides throughput at least the same as the configuration from the basic implementations with the same (or better) accuracy.
The results in Figure 3 show that RASW provides new configurations that prevail over the configurations of the underlying implementations. This means that the same (or better) feedback can be achieved with greater accuracy, and that the same (or better) accuracy can be achieved with a smaller amount of computation. For example, the Pareto-minimal configuration of the implementation of OpenCV 1 with the parameters s = 1.2 and γ = 4 (the second X-sign from above in Fig. 3 (b)). Such a point results in F1-score = 87.9 and bandwidth = 6.1 frames per second. Choosing Δ _{x, t1} = 5, Δ _{x, t2} = 10, Δ _{y, t1} = 5, Δ _{y, t2} = 5, s = 1.3 and γ = 4, the RASW approach leads to better accuracy (F1-score = 88.4) and 2.03x acceleration (throughput = 12.4 frames per second). Point with a black circle in Fig. 3 (b).

The performance gain of the RASW approach is not permanent, i.e. it varies depending on the position in the project space. The purpose of this work is to show that with the help of RASW, the designer of the object detector has the ability to choose the points that most closely match the target application. For example, suppose the target application needs a bandwidth of at least 10 frames per second, with a recall greater than 80% and an accuracy greater than 95%. Then, by selecting the set of parameters mentioned above for the RASW, the designer will get a conditional point corresponding to the black circle in Fig. 3 (b), characterized by a response = 82.4%, accuracy = 95.2% and performance = 12.4 frames per second, which meets the requirements of the system. This point is unattainable for any of the basic implementations.

findings

This article proposes the use of adaptive scanning window motion (RASW) to improve the object detection process. The results for the implementation of the Viola-Jones face detector are presented, but this optimization can be applied to any object detection algorithm that uses a scanning window and a cascade classifier. Compared to existing approaches, RASW provides better performance in the recall / precision and F1-score / throughput spaces, which is especially important for real-time applications. The proposed optimization allows to achieve greater accuracy than existing implementations, but with a smaller amount of computation, and can also be used in conjunction with parallelization, to improve performance. In future work, we plan to develop algorithms for finding the optimal parameters that meet the specified requirements. The proposed algorithm uses data locality to improve face recognition. When capturing an image from a video, temporal non-uniformity can also be taken into account to further reduce the amount of computation.

Literature

[1] C. Zhang and Z. Zhang, “A survey of recent advances in face detection,” in Technical report MSR-TR-2010-66, 2010.
[2] P. Viola and M. Jones, “Rapid object detection using a boosted cascade of simple features,” in CVPR, 2001.
[3] J. Cho, B. Benson, S. Mirzaei, and R. Kastner, “Parallelized Architecture for Multiple Face Detection,” in ASAP, 2009.
[4] M. Hiromoto, H. Sugano, and R. Miyamoto, “Partially parallel architecture for adaboost-based detection with haar-like features,” IEEE Trans. Circuits Syst. Video Technol., Vol. 19, pp. 41–52, 2009.
[5] B. Brousseau and J. Rose, “An energy-efficient, fast FPGA hardware architecture for OpenCV-compatible object detection,” in FPT, 2012.
[6] D. Hefenbrock, J. Oberg, N. Thanh, R. Kastner, and S. Baden, “Accelerating Viola-Jones face detection to FPGA-level using GPUs,” in FCCM, 2010.
[7] D. Oro, C. Fern´andez, JR Saeta, X. Martorell, and J. Hernando, “Real-time GPU-based face detection in HD video sequences,”
in ICCV Workshops, 2011.
[8] SC Tek and M. Gokmen, “GPU accelerated real-time detection of videos using the modified census transform,” in VISAPP, 2012.
[9] L. Acasandrei and A. Barriga, “Accelerating Viola-Jones face detection for embedded and SoC environments,” in ICDSC, 2011.
[10] C. Lampert, M. Blaschko, and T. Hofmann, “Beyond the sliding windows: object localization by efficient subwindow search,”
in CVPR, 2008.
[11] NJ Butko and JR Movellan, “Optimal scanning for faster objectdetection,” in CVPR, 2009.
[12] VB Subburaman and S. Marcel, “Alternative search techniques for face detection, using computer scans,” Comput. Vision Image Understanding, vol. 117, no. 5, pp. 551–570, 2013.
[13] V. Jain and E. Learned-Miller, “FDDB: A benchmark for face detection in unconstrained settings,” University of Massachusetts, Amherst, Tech.
Rep. UM-CS-2010-009, 2010.
[14] G. Bradski, “The OpenCV Library,” Dr. Dobb's J. Softw. Tools, 2000.
[15] H. Rowley, S. Baluja, and T. Kanade, “Neural network-based face detection,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 20, pp. 23-38, 1998.
[16] M. Everingham, LJV Gool, CKI Williams, JM Winn, and A. Zisserman, “The pascal visual object classes (VOC) challenge,” Int. J. Comput. Vision, vol. 88, no. 2, pp. 303–338, 2010.
[17] M. Geilen, T. Basten, BD Theelen, and R. Otten, “An algebra of pareto points,” Fundam. Inform., Vol. 78, no. one,
pp. 35–74, 2007.
[18] C. Goutte and E. Gaussier, “A probabilistic interpretation of precision, recall and score, with implication for evaluation,”
in ECIR, 2005.