In my previous notes, I described the basis on which the lock-free data structures are built, and the basic algorithms for controlling the lifetime of the lock-free data structures. It was a prelude to the description of the actual lock-free containers. But then I ran into the problem: how to build a further story? Just describe the algorithms I know? It's pretty boring: a lot of [pseudo] code, an abundance of details that are important, of course, but very specific. In the end, it is in the published works, to which I give references, and in a much more detailed and rigorous presentation. I wanted to tell interestingly about interesting things, to show the development of approaches to the design of competitive containers.
Well, - I thought, - then the method of presentation should be this: take some type of container - a queue, map, hash map, - and make an overview of the original algorithms for this type of container known today. Where to begin? And then I remembered the simplest data structure - the stack.

It would seem, what can we say about the stack? This is such a trivial data structure that there's nothing much to say.
Indeed, the work on the implementation of the competitive stack is not so much. But on the other hand, those that exist are more devoted to approaches than the actual stack. That approaches me and interest.

Lock-free stack

The stack is probably the first data structure for which the lock-free algorithm was created. It is believed that Treiber published it first in his 1986 article , although there is evidence that this algorithm was first described in the IBM / 360 system documentation.

The algorithm is so simple that I will provide it with the adapted code from libcds (to whom it is interesting - this is the intrusive stack of cds::intrusive::TreiberStack ):

 // m_Top –   bool push( value_type& val ) { back_off bkoff; value_type * t = m_Top.load(std::memory_order_relaxed); while ( true ) { val.m_pNext.store( t, std::memory_order_relaxed ); if (m_Top.compare_exchange_weak(t, &val, std::memory_order_release, std::memory_order_relaxed)) return true; bkoff(); } } value_type * pop() { back_off bkoff; typename gc::Guard guard; // Hazard pointer guard while ( true ) { value_type * t = guard.protect( m_Top ); if ( t == nullptr ) return nullptr ; // stack is empty value_type * pNext = t->m_pNext.load(std::memory_order_relaxed); if ( m_Top.compare_exchange_weak( t, pNext, std::memory_order_acquire, std::memory_order_relaxed )) return t; bkoff(); } } 

This algorithm is repeatedly parsed by the bones (for example, here ), so I will not repeat. A brief description of the algorithm is reduced to the fact that we are using the atomic primitive CAS in m_Top until we get the desired result. Simple and rather primitive.
I note two interesting details:

• Safe memory reclamation (SMR) is needed only in the pop method, since only there we read the m_Top fields. In push no m_Top fields are readable (there is no appeal by the m_Top pointer), so nothing needs to be defended by the Hazard Pointer. This is interesting because usually SMR is required in all methods of the container's lock-free class.
• The mysterious bkoff object and its bkoff() call if the CAS fails.

Here at this very bkoff I would like to dwell upon it.

Back-off strategy

Why is CAS unsuccessful? Obviously because between reading the current value of m_Top and trying to apply CAS, some other thread managed to change the value of m_Top . That is, we have a typical example of competition. In the case of a high load (high contention), when N threads perform push / pop , only one of them will win, the other N - 1 will waste CPU time and interfere with each other on the CAS (recall the MESI cache protocol ).
How to unload the processor when this situation is detected? You can back off from the main task and do something useful or just wait. This is exactly what the back-off strategies are for.
Of course, in the general case “we cannot do something useful” because we have no idea about a specific task, so we can only wait. How to wait? The variant with sleep() discarded - few operating systems can provide us with such small wait timeouts, and the overhead of context switching is too great - more than the CAS execution time.
In the academic environment, the exponential back-off strategy is popular. The idea is very simple:

 class exp_backoff { int const nInitial; int const nStep; int const nThreshold; int nCurrent; public: exp_backoff( int init=10, int step=2, int threshold=8000 ) : nInitial(init), nStep(step), nThreshold(threshold), nCurrent(init) {} void operator()() { for ( int k = 0; k < nCurrent; ++k ) nop(); nCurrent *= nStep; if ( nCurrent > nThreshold ) nCurrent = nThreshold; } void reset() { nCurrent = nInitial; } }; 

That is, we execute nop() in a loop, each time increasing the cycle length. Instead of nop() you can call something more useful, for example, to calculate a bitcoin hint instruction (if one exists) that tells the processor "you have time to do your internal affairs" (again, remember MESI - the processor does may be the sea).
The problem with exponential back-off is simple - it is difficult to find good parameters nInitial , nStep , nThreshold . These constants depend on the architecture and on the task. In the above code, the default values ​​for them are taken from the ceiling.
Therefore, in practice, a fairly good choice for desktop processors and entry-level servers would be yield() back-off - switching to another thread. Thus, we give our time to other, more successful streams, in the hope that they will do what they need and will not disturb us (and we - to them).
Do u even use back-off strategies? Experiments show that it’s about it: the right back-off strategy applied in the right bottleneck can give a performance benefit of the lock-free container at times.
')
The considered back-off strategies help to solve the problem with unsuccessful CAS, but in no way contribute to the implementation of the main task - stack operations. Is it possible to somehow combine push / pop and back-off, so that the back-off strategy actively helps in performing the operation?

Elimination back-off

Consider the problem of unsuccessful CAS in push / pop on the other hand. Why is CAS unsuccessful? Because another thread has changed m_Top . And what does this other thread do? Performs push() or pop() . Now note that the push and pop operations for the stack are complementary: if one thread performs push() and the other at the same time pop() , then in principle there is no point in m_Top to the top of the m_Top stack: the push stream could just transfer your data to a pop stream, while the main property of the stack - LIFO - is not violated. It remains to figure out how to bring both these threads together, bypassing the top of the stack.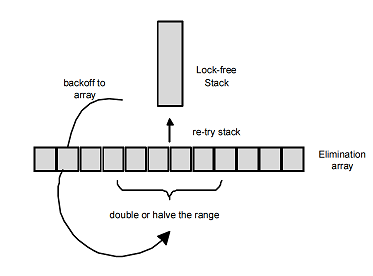


In 2004, Hendler, Shavit, and Yerushalmi proposed a modification of the Treiber algorithm, in which the task of transferring data between push and pop threads without the participation of the top of the stack is solved using a special back-off strategy that they called an exclusion back-off strategy (elimination back -off, I would translate as an absorbing back-off strategy).

There is an elimination array of size N (N is a small number). This array is a member of the stack class. When CAS fails, going back-off, the thread creates a handle to its operation ( push or pop ) and randomly selects an arbitrary cell of this array. If the cell is empty, it writes a pointer to it on its descriptor and performs the usual back-off, for example, exponential. In this case, the stream can be called passive.
If the selected cell already contains a pointer to the P handle of the operation of some other (passive) stream, then the stream (let's call it active) checks what kind of operation it is. If the operations are complementary — push and pop — then they are mutually absorbed:

• if the active thread performs push , then it writes its argument to the P descriptor, thus passing it to the pop operation of the passive stream;
• if the active thread performs pop , then it reads the argument of the complementary push operation from the P handle.

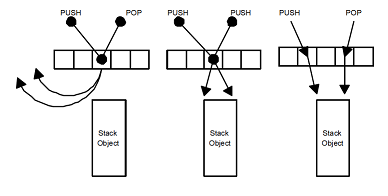
Then, the active thread marks the entry in the elimination array cell as processed, so that the passive stream when exiting the back-off sees that someone has done his job magically. As a result, the active and passive threads execute their operations without referring to the top of the stack .
If, in the selected elimination array cell, the operation is the same (push-push or pop-pop situation), then there is no luck. In this case, the active thread performs the usual back-off and then tries to perform its push / pop as usual, - CAS top of the stack.
Passive stream, after finishing back-off, checks its descriptor in the elimination array. If the descriptor has a mark that the operation is completed, that is, there is another thread with a complementary operation, then the passive stream successfully completes its push / pop .
All the above actions are performed in a lock-free manner, without any locks, so the real algorithm is more complicated than the one described, but the meaning does not change.
The handle contains the operation code — push or pop , —and the operation argument: in the case of push , a pointer to the element to be added, in the case of pop the pointer field remains empty ( nullptr ), if elimination succeeds, a pointer is written to the element of the push absorbing operation.
Elimination back-off allows you to significantly unload the stack under high load, and at low, when the CAS top of the stack is almost always successful, this scheme does not introduce any overhead. The algorithm requires fine tuning, which consists in choosing the optimal size of the elimination array, which depends on the task and the actual load. You can also offer an adaptive version of the algorithm, when the size of the elimination array changes in small limits during operation, adapting to the load.
In the case of imbalance, when the push and pop operations go in bursts - a lot of push without pop , then a lot of pop without push , the algorithm will not give any tangible gain, although there should not be any loss in performance compared to the classic Treiber algorithm .

Flat combining

So far we have been talking about the lock-free stack. Consider now the usual lock-based stack:

 template <class T> class LockStack { std::stack<T *> m_Stack; std::mutex m_Mutex; public: void push( T& v ) { m_Mutex.lock(); m_Stack.push( &v ); m_Mutex.unlock(); } T * pop() { m_Mutex.lock(); T * pv = m_Stack.top(); m_Stack.pop() m_Mutex.unlock(); return pv; } }; 

Obviously, with competing execution, its performance will be very low - all calls to the stack are serialized on the mutex, everything is performed strictly sequentially. Is there any way to improve performance?
If N threads are simultaneously accessing the stack, only one of them will capture the mutex, the rest will wait for it to be released. But instead of waiting passively on a mutex, waiting threads could announce their operations, as in the elimination back-off, and the winning stream (owner of the mutex) could, in addition to its work, perform tasks from its fellows. This idea formed the basis of the flat combining approach, described in 2010 and developing to this day.

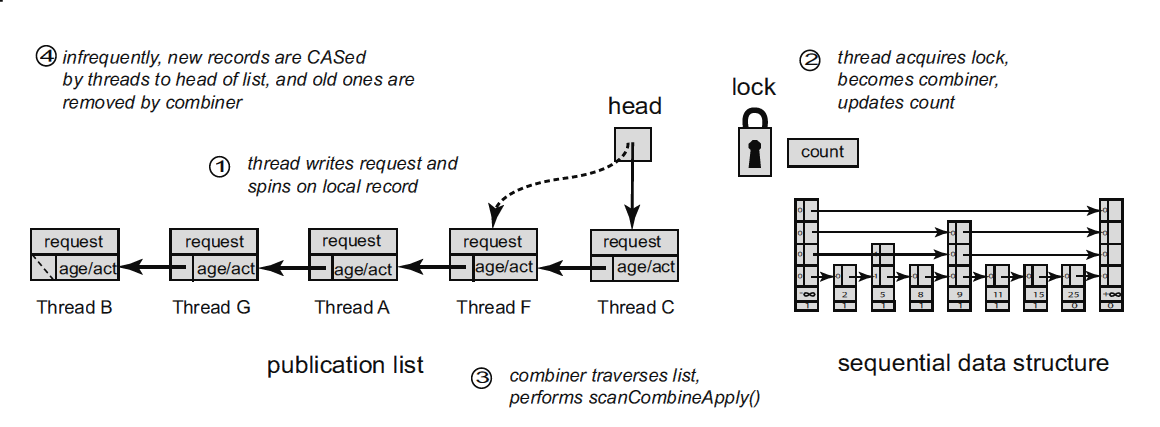
The idea of ​​a flat combining approach can be described as follows. Each data structure, in our case with a stack, is associated with a mutex and a list of announcements (publication list) in a size proportional to the number of threads working with the stack. Each thread at the first access to the stack adds its entry to the list of announcements located in thread local storage (TLS). When executing an operation, the thread publishes a request in its record — an operation ( push or pop ) and its arguments — and tries to capture the mutex. If the mutex is captured, the stream becomes a comber (combiner, not to be confused with a combiner): it scans the list of announcements, collects all requests from it, performs them (in the case of the stack, the elimination considered earlier) writes the result to the elements of the announcement list and finally releases the mutex. If an attempt to capture a mutex fails, the thread waits (spinning) on ​​its announcement when the combiner performs its request and places the result in the announcement record.
The list of announcements is constructed in such a way as to reduce the overhead of its management. The key point is that the list of announcements rarely changes, otherwise we will get a situation where the lock-free publication list is bolted to the stack, which is unlikely to speed up the stack itself. Requests for the operation are made in the already existing list of announcements, which, recall, is the property of the streams and is located in TLS. Some list entries may have the status of “empty”, meaning that the corresponding thread does not currently perform any actions with the data structure (stack). From time to time, the combiner punctures the list of announcements, eliminating long inactive entries (therefore, the list entries must have some timestamp), thereby reducing the time for viewing the list.
In general, flat combining is a very general approach, which successfully extends to complex lock-free data structures and allows combining different algorithms, for example, adding an elimination back-off to the implementation of a flat combining stack. Implementing flat combining in C ++ in a shared library is also a rather interesting task: the fact is that in research papers the list of announcements is usually an attribute of each container object, which can be too expensive in real life, since each container should have your tls entry. I would like to have a more general implementation with a single publication list for all flat combining objects, but it’s important not to lose in speed.

Conclusion

Surprisingly, such a simple data structure as a stack, where it seems to be nothing to write about, allowed us to demonstrate so many interesting approaches to developing competitive data structures!
Back-off strategies are applicable everywhere when constructing lock-free algorithms: as a rule, each operation is enclosed in an infinite loop according to the principle “we do not succeed until it succeeds,” and at the end of the loop body, that is, when the iteration fails, it will not be superfluous put back-off, which can reduce the pressure on the critical data of the container under heavy load.
Elimination back-off is a less general approach, applicable to the stack and, to a lesser extent, to the queue.
Developed in recent years, flat combining is a special trend when building competitive containers - both lock-free and fine grained lock-based.
I hope we will meet with these techniques in the future.