Algorithms about the choice of roads and networks. Steiner networks. Lecture by Vladimir Protasov in Yandex
Today we will talk about one of the first tasks of the theory of large networks, which can be solved completely at the simplest basic level, but which does not become less interesting. This is the problem of the shortest system of roads or the Steiner problem.
It first appeared when there were still no practical needs for large networks: in the thirties of the 20th century. In fact, Steiner began to study it even earlier, in the XIX century. It was a purely geometric problem, the practical applications of which became known only a few decades later.
The conversation will go about that area of mathematics, which subsequently grew into the theory of large networks and divided into several areas. This is an application industry that uses a lot of methods from other mathematical disciplines: discrete mathematics, graph theory, functional analysis, number theory, etc. The rapid development of the theory of large networks came at the end of the nineties and the beginning of the two thousandth. This is of course connected with applied tasks: the development of the Internet, mobile communications, transportation tasks for large cities. In addition, the theory of networks is used in biology (neural networks), in the construction of large electronic circuit boards, etc.
')
The task itself is formulated very simply. There are several points on a plane that need to be connected by a system of roads of the smallest total length so that these roads can be reached from every point to any other. The number of points of course.
It’s worth starting a story with a story about how at the Small Mechmat two groups of students — eighth-graders and eleventh-graders — were given the same task. Four villages are located at the top of a square with a side of four kilometers. Is there a system of roads that would connect all these villages among themselves and have a total length not exceeding 11 kilometers.

If we connect the villages in series, then nothing shorter than the three sides of the square we can think of. With this connection, we will have exactly 12 kilometers. You can connect diagonally, but it will only get worse, because diagonal is longer than the side.

If you put an additional top, then from it you can drive to any four villages. If we take the roads connecting the diametrically opposite vertices, then by the triangle inequality, the sum of their lengths will be greater than the length of the diagonal. Y and the other two the sum of the lengths is also greater than the length of the diagonal. Accordingly, the sum of all roads will be ≥2 4√2 = 8√2≈11.31. Something like this argued eleventh graders who tried to prove the impossibility of the existence of such a system of roads.

At the same time, eighth-graders built a system of roads with the help of a standard ruler with divisions in a nearby audience. And in the end they succeeded. The system is something like the letter H, all angles of which are equal to 120 °. Its length is ≈10.98 kilometers. This is the Steiner network connecting four points. There may be many such networks, maybe a few shortest ones, but such a problem about the shortest system of roads can be solved completely by the methods of elementary geometry.

To finally do away with this task, we find an error in the first solution, where we sort of proved that there can be nothing shorter than 8√2. It was just that this decision did not take into account the possibility to reuse the same area repeatedly.
The Steiner network for the triangle was known 200 years before Jacob Steiner himself, in the seventeenth century. This is the so-called Fermat-Toricelli-Steiner point.
We begin by proving one auxiliary assertion, sometimes called Pompey's theorem. If we take an equilateral triangle on the plane and any other point of the plane, then the sum of the distances to two vertices A and B is always greater than or equal to the distance to the third vertex C: MA + MB ≥ MC. Moreover, MA + MB = MC only if the point M lies on the arc of the circumscribed circle that does not contain the point C. Ie AMB angle should be 120 °. Otherwise, MA + MB> MC.

Of course, if we are talking about an equilateral triangle, in such problems we are often helped by a turn of 60 ° relative to some vertex. We will do this: turn the shaded triangle AMB with respect to vertex A in a clockwise direction. Point B will go to point C, and Point M will go to point M '. As a result, we get that AM = AM '= MM', and M'C = MB. Now we can apply the usual triangle inequality on MM'C. In it, the sum of the two sides of M'M and M'C is greater than MC. Accordingly, MA + MB ≥ MC. And when is equality achieved? Equality is reached when the point M 'exactly hits the direct MC, i.e. when the AMC angle is 120 °.

We now turn directly to the Steiner problem for three points. It is formulated as follows. Triangle set. It is necessary to find a point on the plane, the sum of the distances from which to the vertices of this triangle is the smallest. TA + TB + TC → min.

What is this point? We know several remarkable points of the triangle: the centers of the inscribed and circumscribed circles, the intersection point of the medians, the intersection point of heights. Unfortunately, none of them are suitable for the role of a point with the smallest sum of distances. This point is very special, and is called differently: Toricelli point, Fermat point, Steiner point. It represents a point from which all three vertices of the triangle are visible at identical angles - 120 °. Let us see why this is so. For the first time, the solution of the point problem with the smallest sum of distances to all vertices of a triangle was documented for the first time in the book of the Italian physicist and mathematician Vincenzo Viviani in the middle of the 17th century. However, it is known that the solution to this problem was obtained even earlier by Viviani’s friend, Evangelista Torichelli - both of them were students of Galileo. The solution given in the book was not geometric, it was based on physical principles. This task before Toricelli was known, and perhaps Pierre Fermat decided: they consisted in correspondence, and he learned about this task from Fermat, but it was not known whether the neg had his own solution.
The first geometric solution of this problem appeared only 200 years later, and Jacob Steiner became its author. He was one of the first synthetic geometers who solved geometric problems using exclusively geometric methods. Steiner's solution was based on the Pompeyu theorem we considered above.
Is there even a point from which all the corners of the triangle are visible at an angle of 120 °? It does not always exist, but only if all angles of the triangle are strictly less than 120 °.
If all angles of the triangle are> 120 °, then there is a single Toricelli point. Construct an equilateral triangle to the outer side with respect to the side BC. Construct a circle that would pass through points B, A ', and C. If the Toricelli current exists in this case, then it must lie on this circle, on the arc between points B and C. In the inscribed quad, the sum of the opposite angles is 180 °. The triangle BA'C is equilateral, respectively, all angles in it are equal to 60 °. So, if we put a point on the arc between points B and C, and then complete the quadrilateral, the angle opposite the vertex A 'will be equal to 120 °.
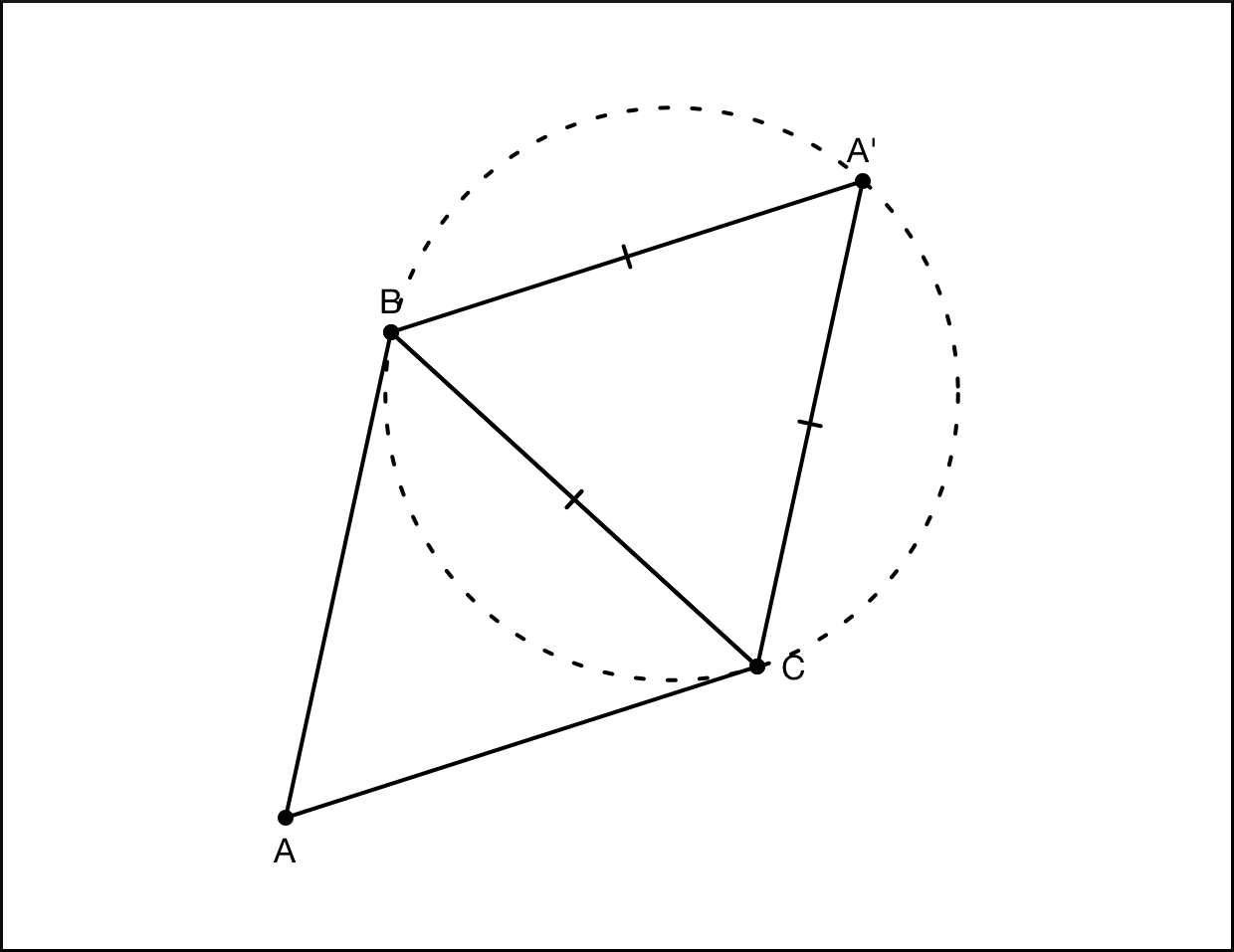
But exactly where to place the point so that all the vertices are visible at an angle of 120 °. We need to build another equilateral triangle, this time relative to the side AC. And in the same way we will enter it in a circle. The point of intersection of the two circles will be the Toricelli point. We have already determined that the BTC angle is 120 °, the ATC angle is obtained in the same way and is also 120 °. In sum, all three corners should give 360 °, which means that the angle of BTA is also equal to 120 °. Thus, we have proved not only the existence of the Toricelli point, but also the fact that it can be only one, since the arcs we have constructed can have at most one intersection point. In theory, the circles could intersect outside the triangle ABC, but this could happen only if at least one of its angles was greater than 120 °.
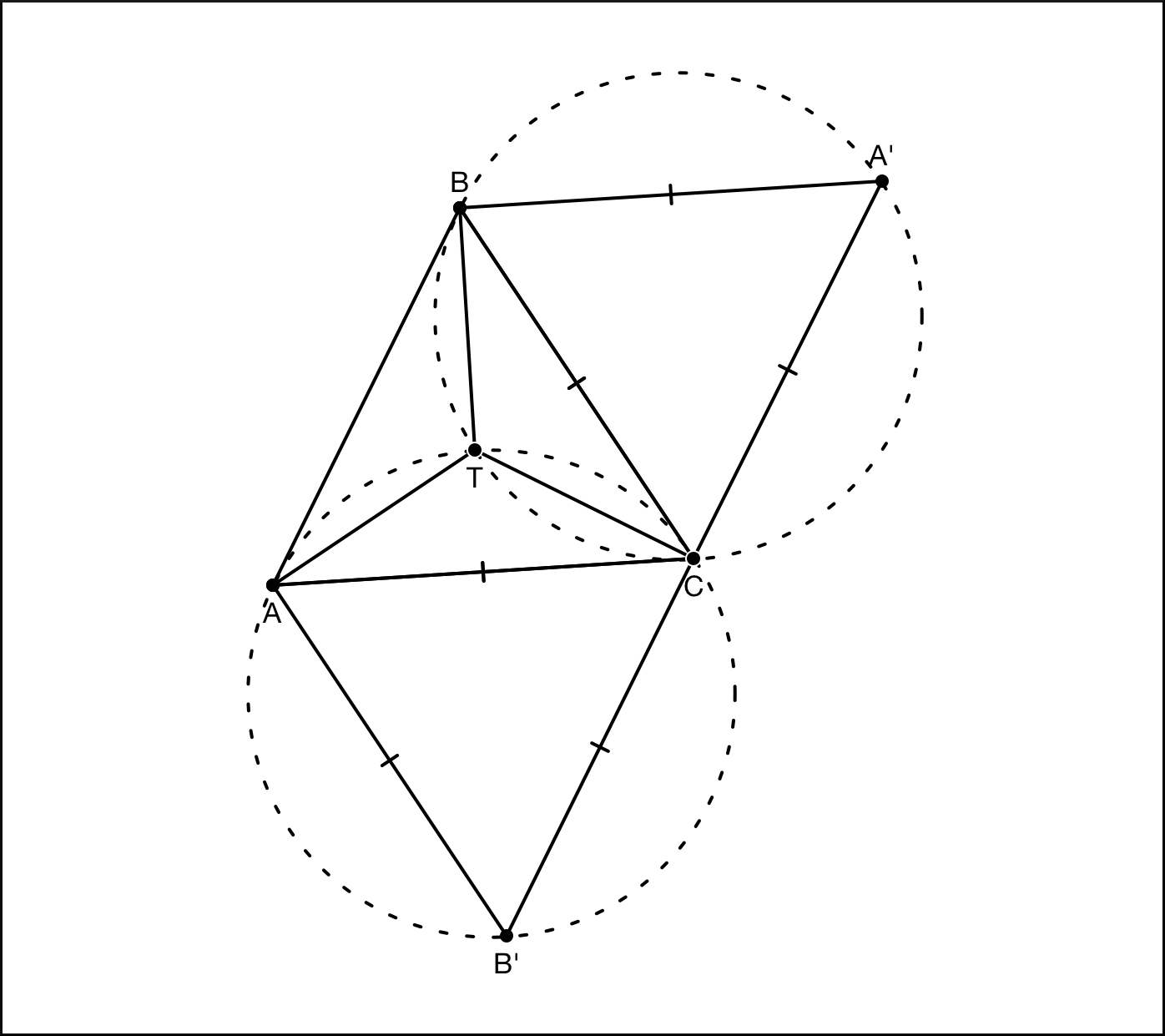
So, we learned how to find the location of the Toricelli point, but did not explain why it can be used to solve the Steiner problem on the minimum sum of distances to the vertices of a triangle. Again, take the triangle ABC, where all angles will be less than 120 ° and construct an external equilateral triangle with respect to the side AC. Let's call it AB'C. Next, we take an arbitrary point M on the plane and connect it with all three vertices of the triangle ABC. By virtue of the Pompey Theorem, MA + MC ≥ MB '. Hence, MA + MB + MC ≥ MB '+ MB, and MB + MB' ≥ BB '. Since MB + MB 'cannot be less than BB', the point M will have the smallest sum of distances to the vertices of the triangle ABC only if MB + MB '= BB'. Under what conditions would such equality be true? According to Pompey's theorem, this requires, first, that MA + MC be equal to MB ', i.e. AMC angle should be equal to 120 °, and secondly, the sum of segments BM and MB 'should be equal to BB', i.e. point M must lie on segment BB '. Accordingly, the angles of AMB and BMC will also be equal to 120 °. From all this it follows that MB + MB '= BB' only in the case when the point M coincides with the Toricelli point. This is the solution of the Steiner problem for three points.

What is the solution to this problem for the case when one of the corners of the triangle is greater than or equal to 120 °? We will not consider in detail the evidence for this option, let us say only that the minimum sum of distances is reached at the apex of the greatest angle of the triangle. Proving it yourself is easy, you just need to take into account all that we have already done above.
It turns out that the Fermat-Toricelli-Steiner point is all that is needed to build systems of roads of the smallest length. The main task is formulated as follows. A finite set (k ≥ 2) of points is given on the plane. It is necessary to connect them with the shortest road system. Steiner himself solved this problem for k = 3 and gave some examples for k = 4. For k ≥ 2, Steiner did not even set a task. For the first time, this task was set 70 years after the death of Jacob Steiner by two Czech mathematicians Kessler and Jarnik. In 1934, the problem was published in a Czech mathematical journal, but for the first few years nobody was interested in it. However, in 1941, two American mathematicians Hurwitz and Courant, who were already known at that time, placed it with reference to Kessler and Yarnik in their book, after which the task became very famous.
Having watched the lecture to the end, you will learn how the Steiner problem is solved in general form on a plane and in space.
It first appeared when there were still no practical needs for large networks: in the thirties of the 20th century. In fact, Steiner began to study it even earlier, in the XIX century. It was a purely geometric problem, the practical applications of which became known only a few decades later.
The conversation will go about that area of mathematics, which subsequently grew into the theory of large networks and divided into several areas. This is an application industry that uses a lot of methods from other mathematical disciplines: discrete mathematics, graph theory, functional analysis, number theory, etc. The rapid development of the theory of large networks came at the end of the nineties and the beginning of the two thousandth. This is of course connected with applied tasks: the development of the Internet, mobile communications, transportation tasks for large cities. In addition, the theory of networks is used in biology (neural networks), in the construction of large electronic circuit boards, etc.
')
The task itself is formulated very simply. There are several points on a plane that need to be connected by a system of roads of the smallest total length so that these roads can be reached from every point to any other. The number of points of course.
It’s worth starting a story with a story about how at the Small Mechmat two groups of students — eighth-graders and eleventh-graders — were given the same task. Four villages are located at the top of a square with a side of four kilometers. Is there a system of roads that would connect all these villages among themselves and have a total length not exceeding 11 kilometers.

If we connect the villages in series, then nothing shorter than the three sides of the square we can think of. With this connection, we will have exactly 12 kilometers. You can connect diagonally, but it will only get worse, because diagonal is longer than the side.

If you put an additional top, then from it you can drive to any four villages. If we take the roads connecting the diametrically opposite vertices, then by the triangle inequality, the sum of their lengths will be greater than the length of the diagonal. Y and the other two the sum of the lengths is also greater than the length of the diagonal. Accordingly, the sum of all roads will be ≥2 4√2 = 8√2≈11.31. Something like this argued eleventh graders who tried to prove the impossibility of the existence of such a system of roads.

At the same time, eighth-graders built a system of roads with the help of a standard ruler with divisions in a nearby audience. And in the end they succeeded. The system is something like the letter H, all angles of which are equal to 120 °. Its length is ≈10.98 kilometers. This is the Steiner network connecting four points. There may be many such networks, maybe a few shortest ones, but such a problem about the shortest system of roads can be solved completely by the methods of elementary geometry.

To finally do away with this task, we find an error in the first solution, where we sort of proved that there can be nothing shorter than 8√2. It was just that this decision did not take into account the possibility to reuse the same area repeatedly.
Three dots
The Steiner network for the triangle was known 200 years before Jacob Steiner himself, in the seventeenth century. This is the so-called Fermat-Toricelli-Steiner point.
We begin by proving one auxiliary assertion, sometimes called Pompey's theorem. If we take an equilateral triangle on the plane and any other point of the plane, then the sum of the distances to two vertices A and B is always greater than or equal to the distance to the third vertex C: MA + MB ≥ MC. Moreover, MA + MB = MC only if the point M lies on the arc of the circumscribed circle that does not contain the point C. Ie AMB angle should be 120 °. Otherwise, MA + MB> MC.

Of course, if we are talking about an equilateral triangle, in such problems we are often helped by a turn of 60 ° relative to some vertex. We will do this: turn the shaded triangle AMB with respect to vertex A in a clockwise direction. Point B will go to point C, and Point M will go to point M '. As a result, we get that AM = AM '= MM', and M'C = MB. Now we can apply the usual triangle inequality on MM'C. In it, the sum of the two sides of M'M and M'C is greater than MC. Accordingly, MA + MB ≥ MC. And when is equality achieved? Equality is reached when the point M 'exactly hits the direct MC, i.e. when the AMC angle is 120 °.

We now turn directly to the Steiner problem for three points. It is formulated as follows. Triangle set. It is necessary to find a point on the plane, the sum of the distances from which to the vertices of this triangle is the smallest. TA + TB + TC → min.

What is this point? We know several remarkable points of the triangle: the centers of the inscribed and circumscribed circles, the intersection point of the medians, the intersection point of heights. Unfortunately, none of them are suitable for the role of a point with the smallest sum of distances. This point is very special, and is called differently: Toricelli point, Fermat point, Steiner point. It represents a point from which all three vertices of the triangle are visible at identical angles - 120 °. Let us see why this is so. For the first time, the solution of the point problem with the smallest sum of distances to all vertices of a triangle was documented for the first time in the book of the Italian physicist and mathematician Vincenzo Viviani in the middle of the 17th century. However, it is known that the solution to this problem was obtained even earlier by Viviani’s friend, Evangelista Torichelli - both of them were students of Galileo. The solution given in the book was not geometric, it was based on physical principles. This task before Toricelli was known, and perhaps Pierre Fermat decided: they consisted in correspondence, and he learned about this task from Fermat, but it was not known whether the neg had his own solution.
The first geometric solution of this problem appeared only 200 years later, and Jacob Steiner became its author. He was one of the first synthetic geometers who solved geometric problems using exclusively geometric methods. Steiner's solution was based on the Pompeyu theorem we considered above.
Is there even a point from which all the corners of the triangle are visible at an angle of 120 °? It does not always exist, but only if all angles of the triangle are strictly less than 120 °.
If all angles of the triangle are> 120 °, then there is a single Toricelli point. Construct an equilateral triangle to the outer side with respect to the side BC. Construct a circle that would pass through points B, A ', and C. If the Toricelli current exists in this case, then it must lie on this circle, on the arc between points B and C. In the inscribed quad, the sum of the opposite angles is 180 °. The triangle BA'C is equilateral, respectively, all angles in it are equal to 60 °. So, if we put a point on the arc between points B and C, and then complete the quadrilateral, the angle opposite the vertex A 'will be equal to 120 °.

But exactly where to place the point so that all the vertices are visible at an angle of 120 °. We need to build another equilateral triangle, this time relative to the side AC. And in the same way we will enter it in a circle. The point of intersection of the two circles will be the Toricelli point. We have already determined that the BTC angle is 120 °, the ATC angle is obtained in the same way and is also 120 °. In sum, all three corners should give 360 °, which means that the angle of BTA is also equal to 120 °. Thus, we have proved not only the existence of the Toricelli point, but also the fact that it can be only one, since the arcs we have constructed can have at most one intersection point. In theory, the circles could intersect outside the triangle ABC, but this could happen only if at least one of its angles was greater than 120 °.

So, we learned how to find the location of the Toricelli point, but did not explain why it can be used to solve the Steiner problem on the minimum sum of distances to the vertices of a triangle. Again, take the triangle ABC, where all angles will be less than 120 ° and construct an external equilateral triangle with respect to the side AC. Let's call it AB'C. Next, we take an arbitrary point M on the plane and connect it with all three vertices of the triangle ABC. By virtue of the Pompey Theorem, MA + MC ≥ MB '. Hence, MA + MB + MC ≥ MB '+ MB, and MB + MB' ≥ BB '. Since MB + MB 'cannot be less than BB', the point M will have the smallest sum of distances to the vertices of the triangle ABC only if MB + MB '= BB'. Under what conditions would such equality be true? According to Pompey's theorem, this requires, first, that MA + MC be equal to MB ', i.e. AMC angle should be equal to 120 °, and secondly, the sum of segments BM and MB 'should be equal to BB', i.e. point M must lie on segment BB '. Accordingly, the angles of AMB and BMC will also be equal to 120 °. From all this it follows that MB + MB '= BB' only in the case when the point M coincides with the Toricelli point. This is the solution of the Steiner problem for three points.

What is the solution to this problem for the case when one of the corners of the triangle is greater than or equal to 120 °? We will not consider in detail the evidence for this option, let us say only that the minimum sum of distances is reached at the apex of the greatest angle of the triangle. Proving it yourself is easy, you just need to take into account all that we have already done above.
It turns out that the Fermat-Toricelli-Steiner point is all that is needed to build systems of roads of the smallest length. The main task is formulated as follows. A finite set (k ≥ 2) of points is given on the plane. It is necessary to connect them with the shortest road system. Steiner himself solved this problem for k = 3 and gave some examples for k = 4. For k ≥ 2, Steiner did not even set a task. For the first time, this task was set 70 years after the death of Jacob Steiner by two Czech mathematicians Kessler and Jarnik. In 1934, the problem was published in a Czech mathematical journal, but for the first few years nobody was interested in it. However, in 1941, two American mathematicians Hurwitz and Courant, who were already known at that time, placed it with reference to Kessler and Yarnik in their book, after which the task became very famous.
Having watched the lecture to the end, you will learn how the Steiner problem is solved in general form on a plane and in space.
Source: https://habr.com/ru/post/215931/
All Articles