Signed Distance Field or how to make a vector out of raster
Today we will talk about the generation of images with a distance map (Signed Distance Field). This type of images is remarkable in that it actually allows you to get "vector" graphics on a video accelerator, and for nothing. One of the first methods of rasterization proposed by Valve in the game Team Fortress 2 for scalable decals in 2007, but still it is not very popular, although it allows rendering fonts of excellent quality using a texture of only 256x256 pixels. This method is perfect for modern high-definition screens and allows you to seriously save on textures in games, it is not picky about hardware and works great on smartphones.

The trick is to create such a specially prepared distance map, that when using the simplest shader, an ideal vector image is obtained. Moreover, using shaders, you can get the effects of shadow, glow, volume, etc.
')
How to create such images? Very simply, ImageMagick allows you to do this in one command:
At this one could put an end, but so a full-fledged topic will not work. Well, under the cut - a description of the fast algorithm for calculating the SDF, an example in C + + and a few shaders for OpenGL.
The first command at the beginning of this post is a recipe for generating SDF from any black and white raster contour. It is based on the new feature of ImageMagick: morphology . Among the morphological transformations present and the calculation of the map of distances .
Calculation of the distance map is the simplest algorithm. It works on monochrome images, where the pixel is either black or white. We consider one of the colors internal, the other - external (as you like, in this picture with a cheetah, the black pixel will be internal). Sometimes they are called the background and foreground colors. For each “internal” pixel of the image, you need to find the “external” pixel closest to it and set the brightness value of this pixel as the Euclidean distance to the nearest “external” pixel. That is, you need to calculate the distance to all the "external" pixels of the image and select the smallest of them. The resulting distance map is called Distance Field (DF), but so far it does not suit us. To get the SDF (Signed DF), we invert the image, repeat the algorithm, invert again and add to the previous result.
The intensity value does not have to be set exactly to the distance value: you can scale the “vagueness” of the image depending on your needs. In particular, for rendering sharp contours it is better to use a less blurred map, and for such special effects as a shadow or a glow it is better to increase the distance map:

And although ImageMagick is not the fastest and easiest way to make such a map, I think this is the best option, since ImageMagick is present on almost all operating systems and is often used by developers for pipelining sprites. It is enough to finish the script a bit and put the generation of images on the stream.
Consider how this works. If you just take and apply the morphology operation to our image, we will not get the best result:

Malevich? No, justblacks steal coal at night, there is not enough contrast, you can quickly pull it out with the

Immediately striking disadvantage: the distance map is generated only outside. This is a consequence of the fact that the algorithm itself is also two-pass, we repeat the same for the negative:
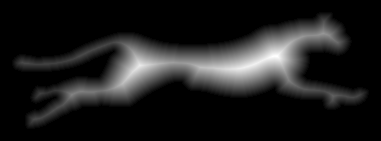
Now the opposite situation - not enough cards outside.
It remains to combine these two algorithms, using the intermediate layer, tighten the contrast and get a furious script from the beginning of the post:
Some explanations:
Well, if there is a higher resolution original - then you can do without a stunt with the scale and scale down only:
Please note that the Jinc filter “moved” to the end of the chain, as it is designed to improve the quality of sampling while reducing the size of the card. Also, do not remove
Some controversial issues .
Does it make sense to "pull" the contrast? In general, theoretically, as the contrast increases, the delta of samples increases, from which antialiasing is then calculated by hardware interpolation. In short, you need to pull out, especially if you plan to display clear smoothed outlines and effects like shadows are not so important. If the original card not only stretches, but also shrinks, you should not get too carried away - otherwise, if you reduce the image, anti-aliasing will deteriorate, achieved due to the blurred edges of the SDF.
How does the quality depend on the resolution of the SDF card? I tried to build a graph of PSNR dependence on the resolution of the map and contrast. In general, the quality increases, but still strongly depends on the contrast of the card. Rate dependencies can be on the graph:
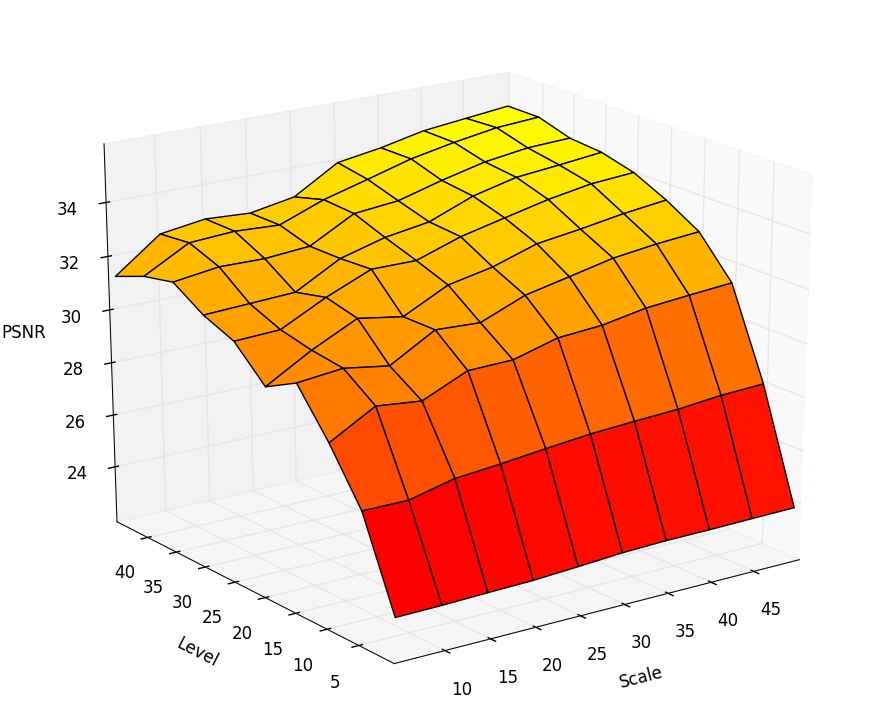
Here Scale is the scale as a percentage of the source, Level - how much the contrast was “stretched”. It can be concluded that the dependence on the scale is not very linear, 30% would be a very compromise option, and the contrast rather strongly affects the quality of the contour.
How much does quality affect the size of the Euclidean filter ? Increasing the size of the filter gives a gain of 0.1 dB + - a penny, in my opinion it is insignificant.
How much can you “shrink” the original image? It strongly depends on the shape. SDF does not like sharp corners, and such a smooth picture as a cheetah from the example feels excellent even on a miniature scale:

The algorithm is simple, but its implementation "head on" will work for hours: in fact, you need to scan the entire image for each pixel. O (N ^ 2) does not suit us at all. But smart people have already thought and came up with an algorithm for the exact (!) Calculation of DF, which works for O (N). It remains to extend the task to the SDF, which is quite simple (see the previous example).
The bottom line. Instead of counting the distance for each pixel, we make two consecutive passes through the image, simply incrementing the distance under certain conditions. This is reminiscent of the fast Box-Blur algorithm. Matan can be learned from [2], but I will try to explain on the fingers.
Pixel p I will call the element of the array N * M, composed of the original image. Pixel is the following structure:
As you can see, there is nothing about brightness, etc. - it is not necessary. The array is formed as follows:
If the pixel of the original image is bright, then
If the pixel of the original image is dark, then
Each pixel has 8 neighbors, we number them like this:
Next, we introduce two auxiliary functions. The function h is needed to calculate the Euclidean distance between the pixel and the neighbor, the function G - to calculate the new value of the distance over the components.
The first pass . This pass is performed in direct order (from the upper left corner of the image to the lower right). Pseudocode:
The second pass . This pass is performed in reverse order (from the lower right corner of the image to the upper left). Pseudocode:
The algorithm must be repeated to negative the original image. Then for the two obtained cards, you need to make the final calculation of the distance and subtraction to combine the two DF cards into one SDF:
Initially, in the structure, we kept the square of the Euclidean distance, so you need to root out. Why do I need to add a unit - do not ask, the result is empirical and without it it turns out crooked :) The final SDF card is the result of subtracting the second from the first, then you need to scale the value as you like.
In my opinion, even an attempt to explain on fingers how it works looks very confusing, so I will provide the source code in C ++. As an input image, I used QImage from Qt so as not to spoil the visibility of the process. The source is based on the source [3], but there are bugs.
The trick is used here: since both passes use a 1-pixel “window”, I add a single-pixel border around the original image to avoid checking borders. For a negative border, you also need to change to the opposite value, which was not considered in [3].
A full-fledged working algorithm can be viewed in the open source UBFG raster font generator. Example result:

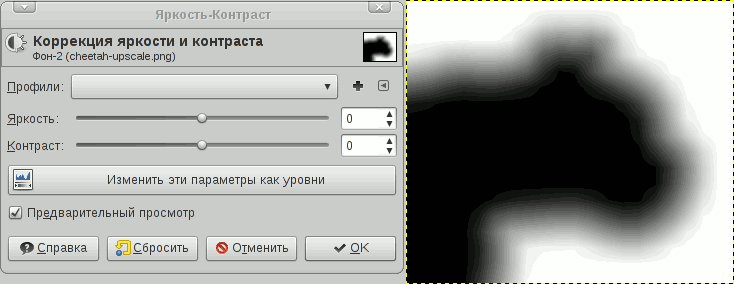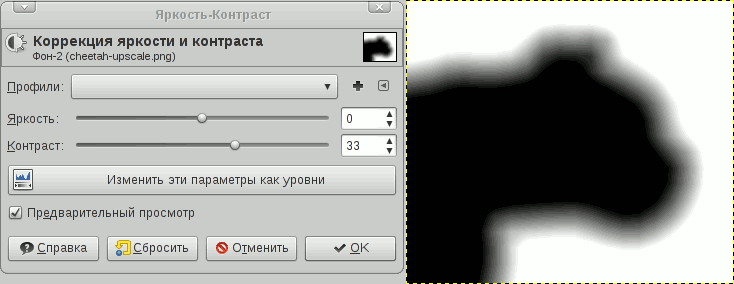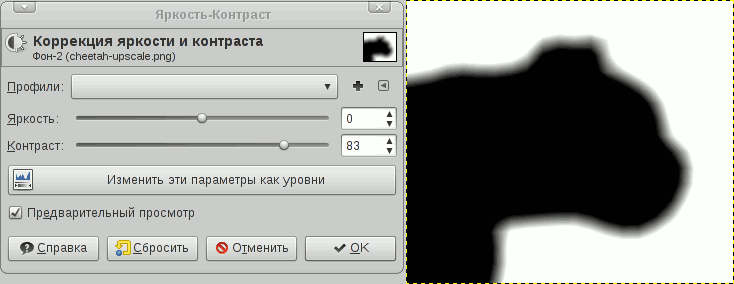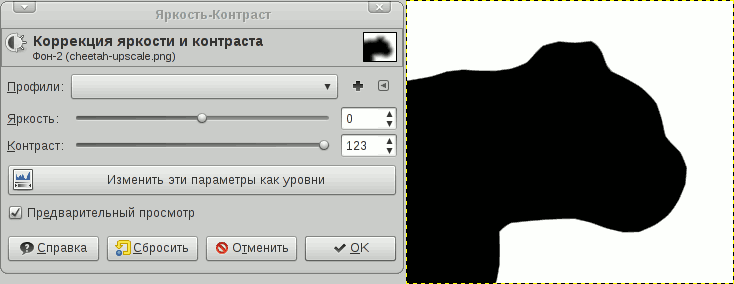
The idea of the inverse transformation (from SDF to raster contour) is based on increasing the contrast to such an extent that the “blurred” edges will not be visible. By changing the contrast of the SDF you can get various effects, as well as adjust the quality of the anti-aliasing of the image. As an example, take the source:

This is also an SDF, just heavily compressed and reduced in size. Increase it 16 times:
Now, to get a beautiful outline, increase the contrast. I used GIMP for this purpose:
To see the result of using SDF in real time, you cannot do without shaders. The simplest alpha test can also be used, but it cuts anti-aliasing at the root. However, the shader used is just a couple of instructions and does not actually affect performance. Moreover, considering that the shaders are now cheap, and the memory / cache is expensive - you can get a good acceleration by saving video memory.
Now let's see how this thing can be used in OpenGL. All examples will be given in the form of pure GLSL source code. You can try in any shader editor. I tested all the examples in the Kick.js editor , since this is the only editor that allows you to load your textures.
Here we simply draw the contrast relative to the average value (0.5). The strength of the contrast should vary depending on the scale of the texture and the smearing of the DF card — the parameter is chosen experimentally and is set in uniform with a scale multiplier.
You can slightly improve the quality with a
Here the threshold also needs to be picked up.
To get this effect, you need to take two thresholds and invert the color:
Result:

Just pohimichit above the previous example - and we get a glow effect:
To make a shadow, you need to take the color for the glow with an offset:
Result:

The result may not seem so hot, but this is because I used a too small map:

[1] Improved Alpha-Tested Magnification for Vector Textures and Special Effects - that same article from Valve.
[2] Frank Y. Shih, Yi-Ta Wu. Fast Euclidean distance scans using a 3x3 neighborhood - Chinese? No, just the University of New Jersey.
[3] www.codersnotes.com/notes/signed-distance-fields - this is also a fairly fast algorithm, but unfortunately its author made several errors and there is multiplication, which is slightly slower than the algorithm presented in this article.
[4] contourtextures.wikidot.com is another implementation of the SDF calculation, but its advantage is that it can take edge smoothing into account to determine the nearest points. Nothing is said about performance, but it's good when there is no possibility to get a high resolution original (on the other hand, you can just do the trick with upscale). If there was an experience of use - unsubscribe in the comments.
[5] gpuhacks.wordpress.com/2013/07/08/signed-distance-field-rendering-of-color-bit-planes - a method for rendering color vector images (suitable for a small number of colors).
[6] distance.sourceforge.net is an interesting resource where various SDF calculation algorithms are compared.
upd . Thanks to the remark of Bas1l, the algorithm is still not entirely accurate and may give errors in calculating the distance to the nearest neighbors due to an error in the proof. This article presents an improved version of the algorithm.
upd2 . From user achkasov note on the part of the shaders. In case of abrupt transitions on the SDF card, heats and uneven anti-aliasing may appear. Learn more about the effect and how to deal with it: iquilezles.org/www/articles/distance/distance.htm
Changing the shader, we get a significant improvement in the area, ahem, tail:


The trick is to create such a specially prepared distance map, that when using the simplest shader, an ideal vector image is obtained. Moreover, using shaders, you can get the effects of shadow, glow, volume, etc.
')
How to create such images? Very simply, ImageMagick allows you to do this in one command:
convert in.png -filter Jinc -resize 400% -threshold 30% \( +clone -negate -morphology Distance Euclidean -level 50%,-50% \) -morphology Distance Euclidean -compose Plus -composite -level 45%,55% -resize 25% out.png At this one could put an end, but so a full-fledged topic will not work. Well, under the cut - a description of the fast algorithm for calculating the SDF, an example in C + + and a few shaders for OpenGL.
What was that spell?
The first command at the beginning of this post is a recipe for generating SDF from any black and white raster contour. It is based on the new feature of ImageMagick: morphology . Among the morphological transformations present and the calculation of the map of distances .
Calculation of the distance map is the simplest algorithm. It works on monochrome images, where the pixel is either black or white. We consider one of the colors internal, the other - external (as you like, in this picture with a cheetah, the black pixel will be internal). Sometimes they are called the background and foreground colors. For each “internal” pixel of the image, you need to find the “external” pixel closest to it and set the brightness value of this pixel as the Euclidean distance to the nearest “external” pixel. That is, you need to calculate the distance to all the "external" pixels of the image and select the smallest of them. The resulting distance map is called Distance Field (DF), but so far it does not suit us. To get the SDF (Signed DF), we invert the image, repeat the algorithm, invert again and add to the previous result.
The intensity value does not have to be set exactly to the distance value: you can scale the “vagueness” of the image depending on your needs. In particular, for rendering sharp contours it is better to use a less blurred map, and for such special effects as a shadow or a glow it is better to increase the distance map:

And although ImageMagick is not the fastest and easiest way to make such a map, I think this is the best option, since ImageMagick is present on almost all operating systems and is often used by developers for pipelining sprites. It is enough to finish the script a bit and put the generation of images on the stream.
Consider how this works. If you just take and apply the morphology operation to our image, we will not get the best result:
convert nosdf.png -morphology Distance Euclidean sdf.png 
Malevich? No, just
-auto-level parameter: convert nosdf.png -morphology Distance Euclidean -auto-level sdf.png 
Immediately striking disadvantage: the distance map is generated only outside. This is a consequence of the fact that the algorithm itself is also two-pass, we repeat the same for the negative:
convert nosdf.png -negate -morphology Distance Euclidean -auto-level sdf.png 
Now the opposite situation - not enough cards outside.
It remains to combine these two algorithms, using the intermediate layer, tighten the contrast and get a furious script from the beginning of the post:
convert in.png -filter Jinc -resize 400% -threshold 30% \( +clone -negate -morphology Distance Euclidean -level 50%,-50% \) -morphology Distance Euclidean -compose Plus -composite -level 45%,55% -resize 25% out.png Some explanations:
-resize 400% - increase the original image to eliminate jagged edges. The algorithm works only for black and white images and I would like to somehow take anti-aliasing into account. But I would recommend to always have on hand an original of four times the size or more. Valve, for example, uses a 4K image for the demonstration, from which it receives a 64x64 SDF. This is certainly a bust. I find an acceptable ratio of 8: 1.-level 45%,55% - you can adjust the degree of blurring of the distance map, by default it is very vague.-filter Jinc and -threshold 30% - experimentally, this filter and the threshold provide the best fit to the original image. Under the spoiler script and source for those who want to check.Script to find the best PSNR metrics
Naturally, the only right option can not be, but I left Jinc 30% as the most average option, which gives an acceptable result.
Picture:

Script:
Picture:

Script:
#!/bin/sh convert orig.png -resize 25% .orig-downscaled.png convert orig.png -threshold 50% .orig-threshold.png SIZE=$(identify orig.png| cut -d' ' -f3) MAX=0.0 MAXRES="" for filter in $(convert -list filter) do for threshold in $(seq 1 99) do convert .orig-downscaled.png -filter $filter -resize $SIZE! -threshold $threshold% .tmp.png PSNR=$(compare -metric PSNR .orig-threshold.png .tmp.png /dev/null 2>&1) if [ "$(echo "$MAX < $PSNR" | bc -l)" = "1" ] then MAXRES="$PSNR $filter $threshold" echo $MAXRES MAX=$PSNR fi rm .tmp.png done done rm .orig-threshold.png .orig-downscaled.png Well, if there is a higher resolution original - then you can do without a stunt with the scale and scale down only:
convert in.png -threshold 50% \( +clone -negate -morphology Distance Euclidean -level 50%,-50% \) -morphology Distance Euclidean -compose Plus -composite -level 45%,55% -filter Jinc -resize 10% out.png Please note that the Jinc filter “moved” to the end of the chain, as it is designed to improve the quality of sampling while reducing the size of the card. Also, do not remove
-threshold 50% - Euclidean does not work correctly for non-monochrome images.Some controversial issues .
Does it make sense to "pull" the contrast? In general, theoretically, as the contrast increases, the delta of samples increases, from which antialiasing is then calculated by hardware interpolation. In short, you need to pull out, especially if you plan to display clear smoothed outlines and effects like shadows are not so important. If the original card not only stretches, but also shrinks, you should not get too carried away - otherwise, if you reduce the image, anti-aliasing will deteriorate, achieved due to the blurred edges of the SDF.
How does the quality depend on the resolution of the SDF card? I tried to build a graph of PSNR dependence on the resolution of the map and contrast. In general, the quality increases, but still strongly depends on the contrast of the card. Rate dependencies can be on the graph:

Here Scale is the scale as a percentage of the source, Level - how much the contrast was “stretched”. It can be concluded that the dependence on the scale is not very linear, 30% would be a very compromise option, and the contrast rather strongly affects the quality of the contour.
How much does quality affect the size of the Euclidean filter ? Increasing the size of the filter gives a gain of 0.1 dB + - a penny, in my opinion it is insignificant.
How much can you “shrink” the original image? It strongly depends on the shape. SDF does not like sharp corners, and such a smooth picture as a cheetah from the example feels excellent even on a miniature scale:
Implementing a fast C ++ algorithm
The algorithm is simple, but its implementation "head on" will work for hours: in fact, you need to scan the entire image for each pixel. O (N ^ 2) does not suit us at all. But smart people have already thought and came up with an algorithm for the exact (!) Calculation of DF, which works for O (N). It remains to extend the task to the SDF, which is quite simple (see the previous example).
The bottom line. Instead of counting the distance for each pixel, we make two consecutive passes through the image, simply incrementing the distance under certain conditions. This is reminiscent of the fast Box-Blur algorithm. Matan can be learned from [2], but I will try to explain on the fingers.
Pixel p I will call the element of the array N * M, composed of the original image. Pixel is the following structure:
{ x, y - f - } As you can see, there is nothing about brightness, etc. - it is not necessary. The array is formed as follows:
If the pixel of the original image is bright, then
x = y = 9999 f = 9999 * 9999 If the pixel of the original image is dark, then
x = y = f = 0 Each pixel has 8 neighbors, we number them like this:
2 3 4 1 p 5 8 7 6 Next, we introduce two auxiliary functions. The function h is needed to calculate the Euclidean distance between the pixel and the neighbor, the function G - to calculate the new value of the distance over the components.
h(p, q) { if q - 1 5 {return 2 * qx + 1} if q - 3 7 {return 2 * qy + 1} {return 2 * (qx + qy + 1)} } G(p, q) { if q - 1 5 {return (1, 0)} if q - 3 7 {return (0, 1)} {return (1, 1)} } The first pass . This pass is performed in direct order (from the upper left corner of the image to the lower right). Pseudocode:
p { q 1 4 { if (h(p, q) + qf < pf) { pf = h(p, q) + qf (px, py) = (qx + qy) + G(p, q) } } } The second pass . This pass is performed in reverse order (from the lower right corner of the image to the upper left). Pseudocode:
p { q 5 8 { if (h(p, q) + qf < pf) { pf = h(p, q) + qf (px, py) = (qx + qy) + G(p, q) } } } The algorithm must be repeated to negative the original image. Then for the two obtained cards, you need to make the final calculation of the distance and subtraction to combine the two DF cards into one SDF:
d1 = sqrt(p1.f + 1); d2 = sqrt(p2.f + 1); d = d1 - d2; Initially, in the structure, we kept the square of the Euclidean distance, so you need to root out. Why do I need to add a unit - do not ask, the result is empirical and without it it turns out crooked :) The final SDF card is the result of subtracting the second from the first, then you need to scale the value as you like.
In my opinion, even an attempt to explain on fingers how it works looks very confusing, so I will provide the source code in C ++. As an input image, I used QImage from Qt so as not to spoil the visibility of the process. The source is based on the source [3], but there are bugs.
Source code
#include <QPainter> #include <stdio.h> #include <math.h> struct Point { short dx, dy; int f; }; struct Grid { int w, h; Point *grid; }; Point pointInside = { 0, 0, 0 }; Point pointEmpty = { 9999, 9999, 9999*9999 }; Grid grid[2]; static inline Point Get(Grid &g, int x, int y) { return g.grid[y * (gw + 2) + x]; } static inline void Put(Grid &g, int x, int y, const Point &p) { g.grid[y * (gw + 2) + x] = p; } static inline void Compare(Grid &g, Point &p, int x, int y, int offsetx, int offsety) { int add; Point other = Get(g, x + offsetx, y + offsety); if(offsety == 0) { add = 2 * other.dx + 1; } else if(offsetx == 0) { add = 2 * other.dy + 1; } else { add = 2 * (other.dy + other.dx + 1); } other.f += add; if (other.f < pf) { pf = other.f; if(offsety == 0) { p.dx = other.dx + 1; p.dy = other.dy; } else if(offsetx == 0) { p.dy = other.dy + 1; p.dx = other.dx; } else { p.dy = other.dy + 1; p.dx = other.dx + 1; } } } static void GenerateSDF(Grid &g) { for (int y = 1; y <= gh; y++) { for (int x = 1; x <= gw; x++) { Point p = Get(g, x, y); Compare(g, p, x, y, -1, 0); Compare(g, p, x, y, 0, -1); Compare(g, p, x, y, -1, -1); Compare(g, p, x, y, 1, -1); Put(g, x, y, p); } } for(int y = gh; y > 0; y--) { for(int x = gw; x > 0; x--) { Point p = Get(g, x, y); Compare(g, p, x, y, 1, 0); Compare(g, p, x, y, 0, 1); Compare(g, p, x, y, -1, 1); Compare(g, p, x, y, 1, 1); Put(g, x, y, p); } } } static void dfcalculate(QImage *img, int distanceFieldScale) { int x, y; int w = img->width(), h = img->height(); grid[0].w = grid[1].w = w; grid[0].h = grid[1].h = h; grid[0].grid = (Point*)malloc(sizeof(Point) * (w + 2) * (h + 2)); grid[1].grid = (Point*)malloc(sizeof(Point) * (w + 2) * (h + 2)); /* create 1-pixel gap */ for(x = 0; x < w + 2; x++) { Put(grid[0], x, 0, pointInside); Put(grid[1], x, 0, pointEmpty); } for(y = 1; y <= h; y++) { Put(grid[0], 0, y, pointInside); Put(grid[1], 0, y, pointEmpty); for(x = 1; x <= w; x++) { if(qGreen(img->pixel(x - 1, y - 1)) > 128) { Put(grid[0], x, y, pointEmpty); Put(grid[1], x, y, pointInside); } else { Put(grid[0], x, y, pointInside); Put(grid[1], x, y, pointEmpty); } } Put(grid[0], w + 1, y, pointInside); Put(grid[1], w + 1, y, pointEmpty); } for(x = 0; x < w + 2; x++) { Put(grid[0], x, h + 1, pointInside); Put(grid[1], x, h + 1, pointEmpty); } GenerateSDF(grid[0]); GenerateSDF(grid[1]); for(y = 1; y <= h; y++) for(x = 1; x <= w; x++) { double dist1 = sqrt((double)(Get(grid[0], x, y).f + 1)); double dist2 = sqrt((double)(Get(grid[1], x, y).f + 1)); double dist = dist1 - dist2; // Clamp and scale int c = dist * 64 / distanceFieldScale + 128; if(c < 0) c = 0; if(c > 255) c = 255; img->setPixel(x - 1, y - 1, qRgb(c,c,c)); } free(grid[0].grid); free(grid[1].grid); } The trick is used here: since both passes use a 1-pixel “window”, I add a single-pixel border around the original image to avoid checking borders. For a negative border, you also need to change to the opposite value, which was not considered in [3].
A full-fledged working algorithm can be viewed in the open source UBFG raster font generator. Example result:

Shader
The idea of the inverse transformation (from SDF to raster contour) is based on increasing the contrast to such an extent that the “blurred” edges will not be visible. By changing the contrast of the SDF you can get various effects, as well as adjust the quality of the anti-aliasing of the image. As an example, take the source:
This is also an SDF, just heavily compressed and reduced in size. Increase it 16 times:
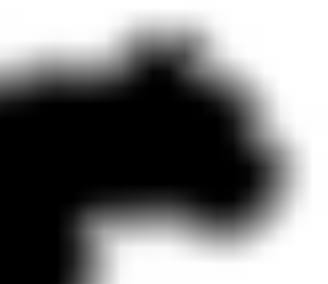
Now, to get a beautiful outline, increase the contrast. I used GIMP for this purpose:

To see the result of using SDF in real time, you cannot do without shaders. The simplest alpha test can also be used, but it cuts anti-aliasing at the root. However, the shader used is just a couple of instructions and does not actually affect performance. Moreover, considering that the shaders are now cheap, and the memory / cache is expensive - you can get a good acceleration by saving video memory.
Now let's see how this thing can be used in OpenGL. All examples will be given in the form of pure GLSL source code. You can try in any shader editor. I tested all the examples in the Kick.js editor , since this is the only editor that allows you to load your textures.
The simplest quick option
precision highp float; uniform sampler2D tex; const float contrast = 40.; void main(void) { vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.3).xxx; gl_FragColor = vec4((c-0.5)*contrast,1.0); } Here we simply draw the contrast relative to the average value (0.5). The strength of the contrast should vary depending on the scale of the texture and the smearing of the DF card — the parameter is chosen experimentally and is set in uniform with a scale multiplier.
You can slightly improve the quality with a
smoothstep filter: precision highp float; uniform sampler2D tex; const float threshold = .01; void main(void) { vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.3).xxx; vec3 res = smoothstep(.5-threshold, .5+threshold, c); gl_FragColor = vec4(res,1.0); } Here the threshold also needs to be picked up.
smoothstep slightly slower on older video cards and phones.Effect outline
To get this effect, you need to take two thresholds and invert the color:
precision highp float; uniform sampler2D tex; const float contrast = 20.; void main(void) { vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.35).xxx; vec3 c1 = (c-.45) * contrast; vec3 c2 = 1.-(c-.5) * contrast; vec3 res = mix(c1, c2, (c-.5)*contrast); gl_FragColor = vec4(res,1.0); } Result:

Glow and shadow effect
Just pohimichit above the previous example - and we get a glow effect:
precision highp float; uniform sampler2D tex; const float contrast = 20.; const float glow = 2.; void main(void) { vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.35).xxx; vec3 c1 = clamp((c-.5)*contrast,0.,1.); vec3 c2 = clamp(1.-(c-.5)/glow, 0., 1.); vec3 res = 1.-mix(c1, c2, (c-.5)*contrast); gl_FragColor = vec4(res,1.0); } To make a shadow, you need to take the color for the glow with an offset:
precision highp float; uniform sampler2D tex; const float contrast = 20.; const float glow = 2.; void main(void) { vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.35).xxx; vec3 gc = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.35 + vec2(-0.02,0.02)).xxx; vec3 c1 = clamp((c-.5)*contrast,0.,1.); vec3 c2 = clamp(1.-(gc-.5)/glow, 0., 1.); vec3 res = 1.-mix(c1, c2, (c-.5)*contrast); gl_FragColor = vec4(res,1.0); } Result:

The result may not seem so hot, but this is because I used a too small map:
Links
[1] Improved Alpha-Tested Magnification for Vector Textures and Special Effects - that same article from Valve.
[2] Frank Y. Shih, Yi-Ta Wu. Fast Euclidean distance scans using a 3x3 neighborhood - Chinese? No, just the University of New Jersey.
[3] www.codersnotes.com/notes/signed-distance-fields - this is also a fairly fast algorithm, but unfortunately its author made several errors and there is multiplication, which is slightly slower than the algorithm presented in this article.
[4] contourtextures.wikidot.com is another implementation of the SDF calculation, but its advantage is that it can take edge smoothing into account to determine the nearest points. Nothing is said about performance, but it's good when there is no possibility to get a high resolution original (on the other hand, you can just do the trick with upscale). If there was an experience of use - unsubscribe in the comments.
[5] gpuhacks.wordpress.com/2013/07/08/signed-distance-field-rendering-of-color-bit-planes - a method for rendering color vector images (suitable for a small number of colors).
[6] distance.sourceforge.net is an interesting resource where various SDF calculation algorithms are compared.
upd . Thanks to the remark of Bas1l, the algorithm is still not entirely accurate and may give errors in calculating the distance to the nearest neighbors due to an error in the proof. This article presents an improved version of the algorithm.
upd2 . From user achkasov note on the part of the shaders. In case of abrupt transitions on the SDF card, heats and uneven anti-aliasing may appear. Learn more about the effect and how to deal with it: iquilezles.org/www/articles/distance/distance.htm
Changing the shader, we get a significant improvement in the area, ahem, tail:

GLSL code
precision highp float; uniform sampler2D tex; const float contrast = 2.; float f(vec2 p) { return texture2D(tex,p).x - 0.5; } vec2 grad(vec2 p) { vec2 h = vec2( 4./256.0, 0.0 ); return vec2( f(p+h.xy) - f(ph.xy), f(p+h.yx) - f(ph.yx) )/(2.0*hx); } void main(void) { vec2 p = gl_FragCoord.xy/vec2(256., 128.)*.35; //float c = texture2D(tex,p).x; float v = f(p); vec2 g = grad(p); float c = (v)/length(g); float res = c * 300.; gl_FragColor = vec4(res,res,res, 1.0); } Source: https://habr.com/ru/post/215905/
All Articles