Rapid generation of random number arrays for simulation, statistical estimation, and re-sampling
Nowadays, simulation modeling using Monte-Carlo methods is used in almost all areas of operations where multiple decisions are needed based on the analysis of data from the outside world. At the same time, the quality, performance and availability of random number generators, which are used to give the abstract method the features of a real problem, solved by an expert, begins to play an important role. As I recently found out, this question begins to play a decisive role in the transition to parallel programming ... You also encountered this problem, and want to know how in Windows you can quickly get arrays of random numbers with the desired distribution?
/ * The article uses a significant number of quotations in English, I assume a sufficient level of reader language preparation * /
One of my applications on duty performs a run of simulation models on a long sequence of factors from the database. Without going into details, the task of studying the probabilistic characteristics of a repetitive binary (two-way) process with a strong element of randomness in the history of its actual implementations in order to reduce uncertainty in predicting future outcomes has arisen recently. Process implementations are considered independent of each other and equally (normally) distributed, the process is considered stationary. The goal — the most accurate prediction of the results of N consecutive process implementations — implies an estimate of the average and lowest expected frequencies of positive process realizations over a period of length N.
Here you can use the standard statistical approach with the calculation of the confidence level at which the implementation of a random variable does not deviate from its expectation by more than k of its standard deviation. This approach is based on the idea of frequency convergence to probabilities ( Bernoulli's theorem ). Of course, it is very tempting to calculate the average values based on several hundred thousand process implementations recorded in the database, but since I have a limit on the subsample length N (on the order of several dozen), the random nature of the process on a limited sample will certainly give me surprises in the form of deviations from average. That is why I need to know, with a given degree of confidence, which maximum possible deviations from the average expected frequency should be “laid down” for a given N.
')
I decided to get the required estimates using the statistical bootstrapping method - multiple generation of samples for N realizations by the Monte Carlo method from the main body of examples. The essence of the method is to form a sufficiently large number of pseudo-samples from the available sample, consisting of random combinations of the original set of elements (as a result, some source elements may occur several times in one pseudo-sample, while others may be absent altogether), and for each resulting pseudo-sample determine the values of the analyzed statistical characteristics in order to study their spread.
According to preliminary estimates, I will need to generate ~ 10 million pseudo-samples for each of the thousands of parameter subgroups. Given the amount of data and other factors, we are talking about dozens of hours of server computing time. Visual Basic 6 has written and tested a prototype simulation application. However, after compiling a multi-stream combat version, it was suddenly discovered that when running the simulation in several threads, the load per CPU core is only 5% instead of the expected 100%.
Basic Hotspots Analysis in the Intel Vtune Amplifier profiler did not show anything unusual. I was sure that the simulator should fully load all the threads with work, because the code did not contain anything except arithmetic operations and memory access at random indexes:
Is this code really tied to the memory bandwidth (memory-bound) ?! Why then do we need multi-megabyte processor caches, why can't they cope ?! The problem baffled me for several days. Belatedly, running Concurrency Analysis revealed a huge drawdown somewhere in the depths of the VB system library, but could not show me where my expensive system functions originate from:
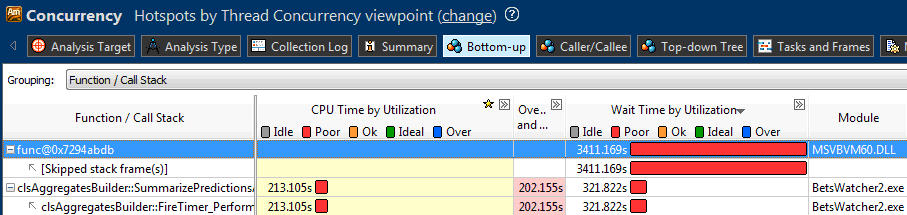
Finally, empirically I found out that the problem was in the Rnd operator! Apparently, the parallel use of Rnd is not provided by the developers; perhaps the Microsoft implementation uses some kind of internal pending locks. In fact, parallelizing Rnd instead of speeding up slowed down the application work THOUSAND times! I think similar behavior will be characteristic of products from the MS Office suite that use VBA. Never before has the question of fast generation of random integer indices was so relevant for me! I decided to look for ready-made libraries to generate arrays of random numbers.
The choice fell on the Intel® Math Kernel Library with its Statistical Functions package.

MKL is available in trial mode. Currently (version 11.02), 11 basic random variable generators, 12 continuous, 11 discrete output distributions are available. What turned out to be very important for me, the developer guarantees the library's thread-safety, moreover, indicates the advantages of its product when used in multi-threaded mode ... In the MKL documentation, my attention was drawn to the following section:
Working examples of the use of random numbers from MKL VSL for simulation modeling under the Xeon Phi co-processor architecture are already available in the network, for example, the article Shuo Li " Case Study: Optimization Framework ." Maybe someone wants to translate this article? Incidentally, in the transition from sequential generation of random numbers to "streaming", a good speed increase is recorded:
Recompiling under the MIC architecture provides an even greater increase compared to the two 8-core Xeons Sandy Bridge @ 2.6 Hz:
True, from the article I did not understand which particular Phi model the author used, apparently, 7120X (16GB, 1.238 GHz, 61 core) for $ 4,129. It's probably time to take Phi, who have not had time before the Knights Landing, guys ;-) It will be interesting to try in battle and “say your fi”.
In any case, we are now interested in the MKL approach to generating blocks of random numbers. First, a vslNewStream call creates a random number generator with given characteristics, for example, the name of the basic generator VSL_BRNG_SFMT19937 (A SIMD-oriented Fast Mersenne Twister pseudorandom number generator) sounds attractive. Then this generator can be used (and from different streams) to directly fill the allocated block of memory with a sequence of random numbers with the desired distribution and data type. A call, for example, virnguniform (method, stream, n, r, a, b) fills the array r based on the generator n with uniformly distributed random values from a to b. After work, the stream should be deleted by calling vslDeleteStream.
There are important aspects in the parallel use / generation of random numbers, due to the finiteness of the period of pseudo-random generators, beautifully painted by our compatriots Sergey Maydanov and Andrey Narakin in the article " Making the Monte Carlo Approach Even Easier and Faster ". For inquisitive cite an excerpt (without translation):
It must be said that in its MKL library, smart guys from Intel implemented skip-ahead and leapfrog approaches to splitting into subsequences. However, within my task, although several streams from the same basic generator are used, there are no requirements for absolute statistical independence of the streams from each other, since they are used independently and on different data subgroups. Therefore, the main technical difficulty for me is to connect the MKL interfaces sharpened for C and Fortran to a Visual Basic project. The article Use Intel® MKL from Microsoft * Office Excel comes to the rescue, which describes how to generate a wrapper dll by the forces of MKL itself, and gives examples of MLK function calls (stdcall convention, of course) from Excel.
The concept is as follows: you can ask MKL Builder to automatically generate a dll, exporting an arbitrary list of MKL functions you need, with a given calling convention. Of course, you can create your own dll project in VC ++, but it seemed to me that automatic generation is a more universal way, and it also helps to get the required file faster. It quickly became clear that the article was out of date, and even the test command nmake libia32 threading = sequential interface = stdcall export = user_example_list name = mkl_custom failed for many reasons. I solved one of the problems by adding the msvcrt.lib file to the mkl \ tools \ builder \ folder. Separately, the multiple messages of unresolved external symbol ___security_cookie delivered pleasure.
Using the recommendations of Microsoft and killing half a day for searches, I came to the conclusion that you need to modify the makefile file in the builder folder, assigning the bufferoverflowU.lib parameter to the linker command line after out: $ (CB_NAME) .dll. Well, then the mechanism with a creak earned, and, issuing nmake libia32 threading = parallel interface = stdcall export = vml_vsl_stdcall_example_list name = mkl_custom , I became the proud owner of a 38-megabyte dynamic library containing all the functions of the Vector Statistical Library. Having conquered a healthy capitalist greed, I left only 3 necessary functions in the library, after which the size was reduced to several megabytes.
Now about the calling code. In VB6 and VBA, the necessary functions should be declared like this:
As a test, we will try to generate an array of 5 million random integer indices from 1 to 10,000 (not including 10,000) 100 times using the VSL_BRNG_MCG31 basic generator (A 31-bit multiplicative congruential generator):
Execution time - 1.19 seconds. By the way, the VSL_BRNG_SFMT19937 generator, which is able to use SSE, copes with this task in 0.99 seconds. Well, add the calls of the necessary operations to the main code, and monitor the processor load:
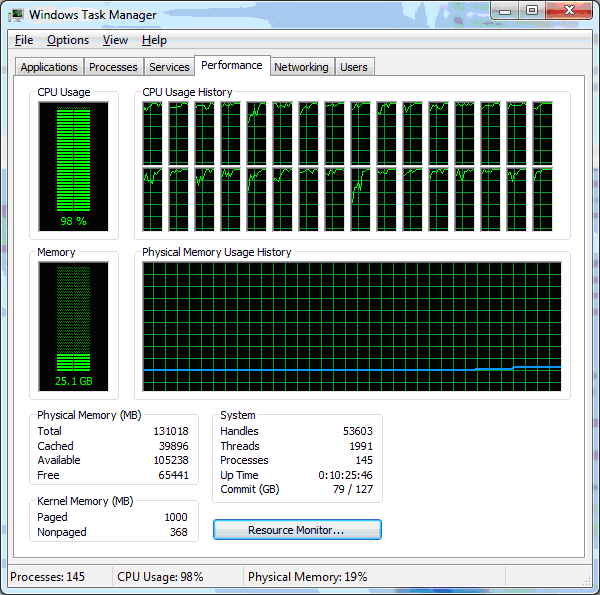
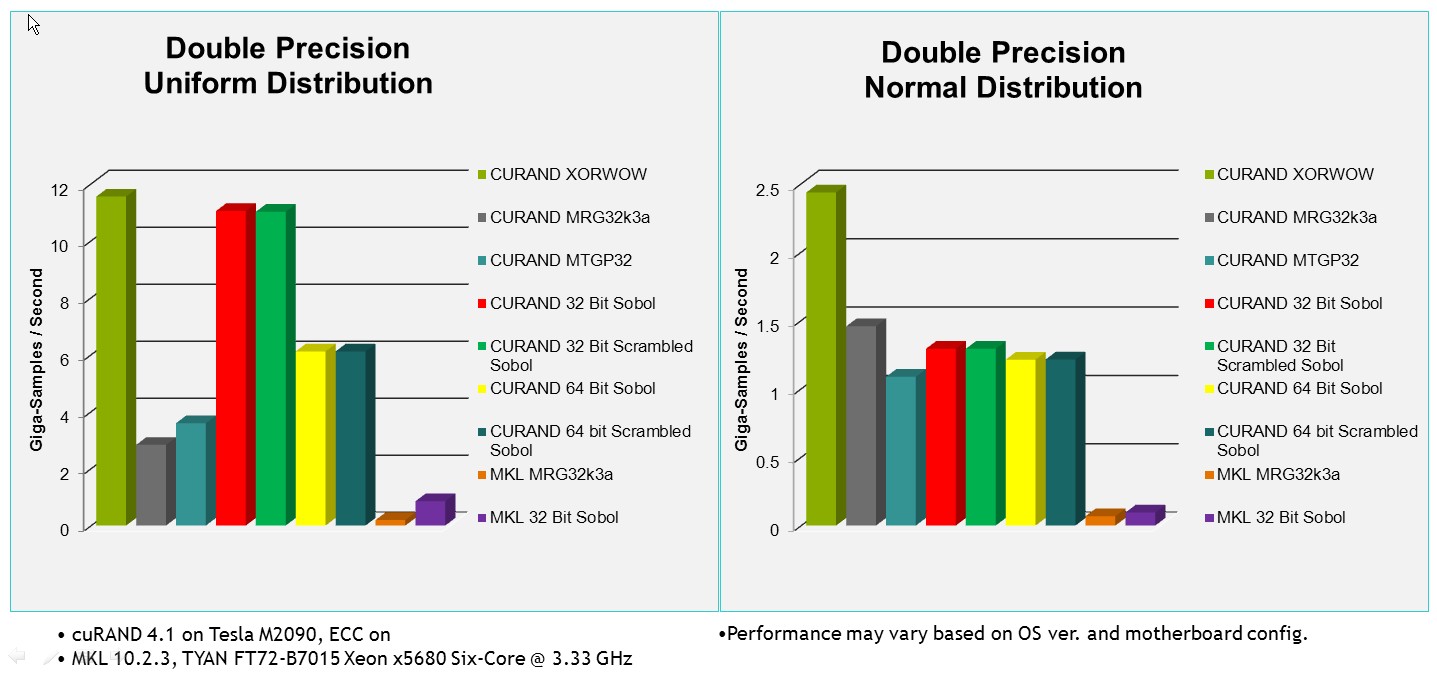
Bingo, full download! It was thought to make a GPGPU implementation using the cuRAND package, whose benefits are clearly indicated by Nvidia:
Blazing Fast cuRAND Performance compared to Intel MKL
However, the initial goal was achieved with the help of MKL, and there is no free time to test the Cuda version. :-)
To summarize: we learned about some of the problems in parallel generation of random numbers, and received practical recommendations for solving them with the help of Intel MKL. You can use this powerful library from any language of modern Visual Studio - C ++, C #, VB, as well as Visual Fortran, and, with the help of the sounded methodology, from any environment that can call external dll, for example, VB6, VBA, LabView, Matlab and many others.
Thanks for attention!
/ * The article uses a significant number of quotations in English, I assume a sufficient level of reader language preparation * /
One of my applications on duty performs a run of simulation models on a long sequence of factors from the database. Without going into details, the task of studying the probabilistic characteristics of a repetitive binary (two-way) process with a strong element of randomness in the history of its actual implementations in order to reduce uncertainty in predicting future outcomes has arisen recently. Process implementations are considered independent of each other and equally (normally) distributed, the process is considered stationary. The goal — the most accurate prediction of the results of N consecutive process implementations — implies an estimate of the average and lowest expected frequencies of positive process realizations over a period of length N.
Here you can use the standard statistical approach with the calculation of the confidence level at which the implementation of a random variable does not deviate from its expectation by more than k of its standard deviation. This approach is based on the idea of frequency convergence to probabilities ( Bernoulli's theorem ). Of course, it is very tempting to calculate the average values based on several hundred thousand process implementations recorded in the database, but since I have a limit on the subsample length N (on the order of several dozen), the random nature of the process on a limited sample will certainly give me surprises in the form of deviations from average. That is why I need to know, with a given degree of confidence, which maximum possible deviations from the average expected frequency should be “laid down” for a given N.
')
I decided to get the required estimates using the statistical bootstrapping method - multiple generation of samples for N realizations by the Monte Carlo method from the main body of examples. The essence of the method is to form a sufficiently large number of pseudo-samples from the available sample, consisting of random combinations of the original set of elements (as a result, some source elements may occur several times in one pseudo-sample, while others may be absent altogether), and for each resulting pseudo-sample determine the values of the analyzed statistical characteristics in order to study their spread.
According to preliminary estimates, I will need to generate ~ 10 million pseudo-samples for each of the thousands of parameter subgroups. Given the amount of data and other factors, we are talking about dozens of hours of server computing time. Visual Basic 6 has written and tested a prototype simulation application. However, after compiling a multi-stream combat version, it was suddenly discovered that when running the simulation in several threads, the load per CPU core is only 5% instead of the expected 100%.
Basic Hotspots Analysis in the Intel Vtune Amplifier profiler did not show anything unusual. I was sure that the simulator should fully load all the threads with work, because the code did not contain anything except arithmetic operations and memory access at random indexes:
For k = 1 To NumIters Randomize For i = 1 To NumPockets NumFired = 0 For j = 1 To chainLength ind = d + Int(B * Rnd) NumFired = NumFired + FiredOrNot(ind) Next j Tmp = NumFired / chainLength If Tmp < MinProb Then MinProb = Tmp If Tmp > MaxProb Then MaxProb = Tmp Values(i) = Tmp TotalFired = TotalFired + NumFired Next i AvgProb = TotalFired / (k * NumPockets) / chainLength Next k Is this code really tied to the memory bandwidth (memory-bound) ?! Why then do we need multi-megabyte processor caches, why can't they cope ?! The problem baffled me for several days. Belatedly, running Concurrency Analysis revealed a huge drawdown somewhere in the depths of the VB system library, but could not show me where my expensive system functions originate from:

Finally, empirically I found out that the problem was in the Rnd operator! Apparently, the parallel use of Rnd is not provided by the developers; perhaps the Microsoft implementation uses some kind of internal pending locks. In fact, parallelizing Rnd instead of speeding up slowed down the application work THOUSAND times! I think similar behavior will be characteristic of products from the MS Office suite that use VBA. Never before has the question of fast generation of random integer indices was so relevant for me! I decided to look for ready-made libraries to generate arrays of random numbers.
The choice fell on the Intel® Math Kernel Library with its Statistical Functions package.

MKL is available in trial mode. Currently (version 11.02), 11 basic random variable generators, 12 continuous, 11 discrete output distributions are available. What turned out to be very important for me, the developer guarantees the library's thread-safety, moreover, indicates the advantages of its product when used in multi-threaded mode ... In the MKL documentation, my attention was drawn to the following section:
Non-deterministic random number generator (RDRAND-based generators only) [AVX], [IntelSWMan]. You can use a non-deterministic random number generator only if the hardware app supports it. If your CPU supports a non-deterministic random number generator, see Chapter 8: Post-32nm Processor Instructions in [AVX] or Chapter 4: RdRand Instruction [BMT].I have long wanted to try this "iron" opportunity, but unfortunately, it turned out that my processors are not equipped with a hardware random number generator. In addition to the above, an important feature of the MKL package is the paradigm of block generation of random number flows, in contrast to the usual practice of obtaining one random value for one operator call in most programming languages.
Working examples of the use of random numbers from MKL VSL for simulation modeling under the Xeon Phi co-processor architecture are already available in the network, for example, the article Shuo Li " Case Study: Optimization Framework ." Maybe someone wants to translate this article? Incidentally, in the transition from sequential generation of random numbers to "streaming", a good speed increase is recorded:
Changing the RNG from C ++ TR1 to MKL, it was not only confirmed
Recompiling under the MIC architecture provides an even greater increase compared to the two 8-core Xeons Sandy Bridge @ 2.6 Hz:
For now it took less than 5 seconds, an instant 8.82X improvement.
True, from the article I did not understand which particular Phi model the author used, apparently, 7120X (16GB, 1.238 GHz, 61 core) for $ 4,129. It's probably time to take Phi, who have not had time before the Knights Landing, guys ;-) It will be interesting to try in battle and “say your fi”.
In any case, we are now interested in the MKL approach to generating blocks of random numbers. First, a vslNewStream call creates a random number generator with given characteristics, for example, the name of the basic generator VSL_BRNG_SFMT19937 (A SIMD-oriented Fast Mersenne Twister pseudorandom number generator) sounds attractive. Then this generator can be used (and from different streams) to directly fill the allocated block of memory with a sequence of random numbers with the desired distribution and data type. A call, for example, virnguniform (method, stream, n, r, a, b) fills the array r based on the generator n with uniformly distributed random values from a to b. After work, the stream should be deleted by calling vslDeleteStream.
There are important aspects in the parallel use / generation of random numbers, due to the finiteness of the period of pseudo-random generators, beautifully painted by our compatriots Sergey Maydanov and Andrey Narakin in the article " Making the Monte Carlo Approach Even Easier and Faster ". For inquisitive cite an excerpt (without translation):
Hidden text
It is an important one. Many Monte Carlo methods allow quite natural parallelization. In this case, the choice of random number generators should be made according to their ability to work in parallel. One important aspect that should not be considered is
independence between sequences generated in parallel. There are a number of methods to generate independent sequences. We consider three of them below.
It was a simultaneous use of several generators, for example, in terms of the spectral test. There is a number of ways to get the number of threads, that is, the number of threads.
One of them is known as the block-splitting or skip-ahead method. There is no need for any additional subsequence. The other method is known as the leapfrog method. This differs from the skip-ahead method to the original sequence of x1, x2, x3, ... into the sequence of generations of the numbers x1, xk + 1, x2k + 1, x3k + 1, ... , the second generates random numbers x2, xk + 2, x2k + 2, x3k + 2, ..., and, finally, the kth generates random numbers xk, x2k, x3k, ...
There are advantages and disadvantages of Monte Carlo methods. It is limited by the number of independent parameters. With the skip-ahead method, it is possible to correct the correlation between the blocks.
When the number of subsequences increases. Finally, for some generators, it was necessary to complete the process. Hence, the most appropriate generators should be selected.
It must be said that in its MKL library, smart guys from Intel implemented skip-ahead and leapfrog approaches to splitting into subsequences. However, within my task, although several streams from the same basic generator are used, there are no requirements for absolute statistical independence of the streams from each other, since they are used independently and on different data subgroups. Therefore, the main technical difficulty for me is to connect the MKL interfaces sharpened for C and Fortran to a Visual Basic project. The article Use Intel® MKL from Microsoft * Office Excel comes to the rescue, which describes how to generate a wrapper dll by the forces of MKL itself, and gives examples of MLK function calls (stdcall convention, of course) from Excel.
The concept is as follows: you can ask MKL Builder to automatically generate a dll, exporting an arbitrary list of MKL functions you need, with a given calling convention. Of course, you can create your own dll project in VC ++, but it seemed to me that automatic generation is a more universal way, and it also helps to get the required file faster. It quickly became clear that the article was out of date, and even the test command nmake libia32 threading = sequential interface = stdcall export = user_example_list name = mkl_custom failed for many reasons. I solved one of the problems by adding the msvcrt.lib file to the mkl \ tools \ builder \ folder. Separately, the multiple messages of unresolved external symbol ___security_cookie delivered pleasure.
Using the recommendations of Microsoft and killing half a day for searches, I came to the conclusion that you need to modify the makefile file in the builder folder, assigning the bufferoverflowU.lib parameter to the linker command line after out: $ (CB_NAME) .dll. Well, then the mechanism with a creak earned, and, issuing nmake libia32 threading = parallel interface = stdcall export = vml_vsl_stdcall_example_list name = mkl_custom , I became the proud owner of a 38-megabyte dynamic library containing all the functions of the Vector Statistical Library. Having conquered a healthy capitalist greed, I left only 3 necessary functions in the library, after which the size was reduced to several megabytes.
Now about the calling code. In VB6 and VBA, the necessary functions should be declared like this:
Public Declare Function vslNewStream Lib "mkl_custom.dll" (ByRef StreamPtr As Long, ByVal brng As Long, ByVal seed As Long) As Long Public Declare Function vslDeleteStream Lib "mkl_custom.dll" (ByRef StreamPtr As Long) As Long Public Declare Function viRngUniform Lib "mkl_custom.dll" (ByVal method As Long, ByVal StreamPtr As Long, ByVal n As Long, ByRef Data As Long, ByVal A As Long, ByVal B As Long) As Long As a test, we will try to generate an array of 5 million random integer indices from 1 to 10,000 (not including 10,000) 100 times using the VSL_BRNG_MCG31 basic generator (A 31-bit multiplicative congruential generator):
Dim i&, theStream&, v&(), res&, t! Dim theStream As Long ReDim v(1 To 5000000): res = vslNewStream(theStream, VSL_BRNG_MCG31, 777) t = Timer For i = 1 To 100 res = viRngUniform(VSL_RNG_METHOD_UNIFORM_STD, theStream, 5000000, v(1), 1, 10000) Next i Debug.Print Timer - t res = vslDeleteStream(theStream) Execution time - 1.19 seconds. By the way, the VSL_BRNG_SFMT19937 generator, which is able to use SSE, copes with this task in 0.99 seconds. Well, add the calls of the necessary operations to the main code, and monitor the processor load:

Bingo, full download! It was thought to make a GPGPU implementation using the cuRAND package, whose benefits are clearly indicated by Nvidia:
Blazing Fast cuRAND Performance compared to Intel MKL

However, the initial goal was achieved with the help of MKL, and there is no free time to test the Cuda version. :-)
To summarize: we learned about some of the problems in parallel generation of random numbers, and received practical recommendations for solving them with the help of Intel MKL. You can use this powerful library from any language of modern Visual Studio - C ++, C #, VB, as well as Visual Fortran, and, with the help of the sounded methodology, from any environment that can call external dll, for example, VB6, VBA, LabView, Matlab and many others.
Thanks for attention!
Source: https://habr.com/ru/post/215775/
All Articles