Bitcoin: Decentralized Electronic Monetary System
I bring to the attention of the community a free translation of the original article by Satoshi Nakamoto "Bitcoin: A Peer-to-Peer Electronic Cash System" .
From the translator:
I am not a professional translator and I don’t understand cryptography, but recently I became interested in Bitcoin technology and wanted to start learning from first principles. A quick search on the Internet did not give me a translation of the main article of Satoshi Nakamoto and I decided to try to translate it myself.
Shortly after the translation was started, I realized that English is probably not native to the author of the article, since sometimes it was extremely difficult to understand what the author means and why there are so many “and” particles in one sentence. However, most of the difficulties were overcome and I decided to present this final product to the public.
Short.
')
Electronic payments on the Internet are almost entirely dependent on financial institutions that are a trusted third party to make a payment. Although the system works well for most transactions, it suffers from a congenital defect: a model based on trust.
Completely non-refundable payments are impossible, since financial institutions cannot avoid disputes with intermediaries. Costs associated with intermediaries increase transaction costs, which leads to the limitation of the minimum transaction size and makes it impractical to make small daily payments. In addition, the price increases due to the impossibility of making non-refundable payments for services that provide non-refundable services. The ability to return requires trusted intermediaries. Sellers are forced to beware of their customers, requiring more information from them than would be required if the possibility of non-refundable payments is possible. A certain percentage of returns is assumed as inevitable. These costs and doubts can be avoided if the buyer uses ordinary money, but there is no mechanism for making payments on the Internet without an intermediary that is trusted.
That is why an electronic payment system is needed, based on cryptographic complexity instead of trust, allowing any two parties to make transfers to each other without trust brokers. Transactions that are almost impossible to undo will protect sellers from fraudsters, and the routine escrow mechanisms can be easily implemented to protect customers. In this article, we propose a solution to the problem of reusable funds using a distributed timestamp server that generates complex-calculated transactions in chronological order. The system is safe as long as the friendly nodes simultaneously control more computing power than any group of attackers.
The chain of digital signatures will be called electronic coins. Each owner sends the coins to the next one, adding a digitally signed hash of the previous transaction and its public key to the end of the chain. The payee can verify the signature (coin) by checking the chain of owners.
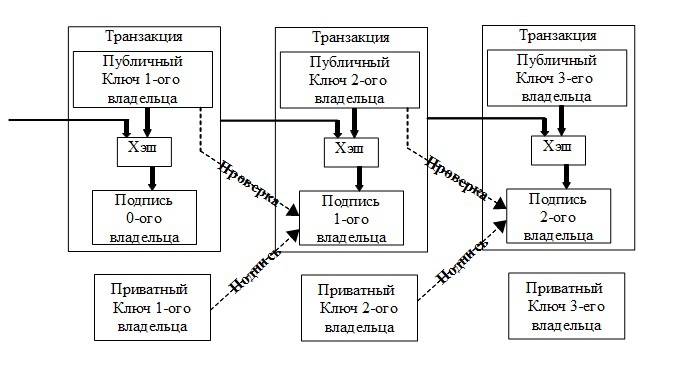
The problem, of course, is that the payee cannot find out if someone from the previous owners had spent the same money twice. Usually this problem is solved by using a trusted centralized intermediary organization that checks each transaction for double spending. After each transaction, the coin must return to the intermediary who, instead of the old one, issues a new coin, then only coins issued by the intermediary are guaranteed not to be spent twice.
The problem with this approach is that the fate of the entire financial system depends on the intermediary company, since all transactions go through it like a bank.
So, you need a way by which the recipient will know that the senders have not paid the same coins with someone else. In our case, only the previous transaction history is important; subsequent attempts to double-use coins do not bother us. The only way to confirm the absence of a transaction is to know all the transactions. In the intermediary model, the intermediary is aware of all transactions and their sequence. To achieve this without a trusted intermediary, all transactions must be known to everyone, i.e. need a system whose members will agree on a single history of all payments. Payment recipients need to verify that during the transaction most participants agree that it was received for the first time.
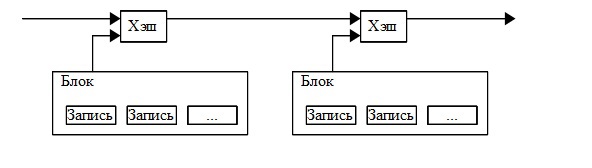
The solution we offer is based on a timestamp server. The job of the timestamp server is to hash a block of records, memorize time and publish a hash. The time stamp is evidence that the data existed at that time and in the order in which they arrived for hashing. Each timestamp includes the previous timestamp in its hash forming a chain, in which each successive timestamp confirms the previous one.
To implement a timestamp server based on a decentralized network, you need to use an algorithm for complex calculations such as Hashcash. Complicated calculations involve finding the value that, when SHA-256 hashes, will give a hash that will start with a large number of zero bits. The average computation time grows exponentially with the number of zero bits, and the result can be verified by calculating a single hash.
For our timestamp server, we implement complex calculations by increasing the special variable (nonce) inside the block by one, until a hash with the required number of zero bits is found. As soon as time is spent for performing complex calculations, the block cannot be changed without doing the calculation again. Since the following blocks form a chain, the work for changing the block includes the work for changing all the following blocks after it.

Checked complex calculations also solve the problem of obtaining confirmation from the majority of participants. A confirmation based on the principle of “one IP address - one vote” can be discredited by anyone who has a lot of IP addresses under control. Checked calculations are essentially "one processor - one vote." Confirmation from the majority is the longest chain, the creation of which was spent the most amount of computing power. If the core computing power is controlled by honest participants, an honest chain will grow faster than any chain of malicious participants. To modify any block, the attacker will have to do the complex calculations associated with this block, as well as all the blocks after it, will need to catch up and overtake honest block builders. We will show further that in a slow attacker, the ability to catch up exponentially decreases with the addition of new blocks.
The following steps describe the network operation:
1) A new transaction is broadcast to all nodes.
2) Each node places new transactions in a block.
3) Each node performs complex calculations to find its block
4) When a node finds a solution for its block, it broadcasts this block to all nodes.
5) A node accepts a block only if all transactions in it are correct and not expired.
6) Consent node to accept the block is expressed in the fact that the node begins work on creating the next block in the chain, using the hash of the received block as the previous hash.
Nodes always perceive the longest chain as correct and work on increasing it. If two nodes simultaneously broadcast different versions of the next block, the nodes may receive each of the versions at different times. In this case, the node starts working with the block that was received earlier, but another version should be saved in case it subsequently becomes a longer chain. Branches can be ignored when the next stage of calculations is completed and one of the branches becomes longer than the others; nodes working with other branches will switch to the longest.
Broadcast sending a new transaction does not have to reach all nodes. It will be included in the block as soon as it reaches many nodes. Broadcast parcel blocks, too, may not reach all. If the node has not received a block, it will request it when it receives the next block to fill in the missing links of the chain.
We agree that the first transaction in the block will be a special transaction that starts a new coin belonging to the creator of the block. This will add an incentive for the nodes to maintain the network and provide a way to initially put coins into circulation, since there is no central authority for their release. The constant addition of new coins is like mining, when resources are spent to add gold to circulation. In our case, CPU time and electricity are consumed.
Stimulus may also be present when transactions are being carried out. If the value at the output of the transaction is less than the value at the input, this difference is added to the stimulus value of the block containing the transaction. When a predetermined number of coins is issued, the stimulation will be made only through transactions, i.e. inflation will completely disappear.
Stimulus encourages nodes to stay honest. If a greedy attacker can gather more computing power than all honest nodes, then he will have to make a choice: to deceive people by stealing their coins or by generating new coins themselves. He will find it more profitable to play by the rules, the rules that will allow him to get more coins than any other combinations and not to undermine the system, and with it his own state.
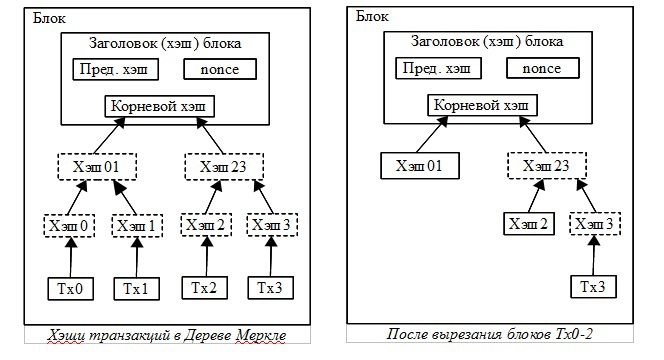
While the last transactions are written to the block, the declined transactions also take up disk space. To fix this without changing block hashes, transactions are hashed into the Merkle Tree, where only the root is included in the block hash. Old blocks can be packed by trimming tree branches. Internal hashes can not be saved.
The block header without transactions takes approximately 80 bytes. If blocks are generated every 10 minutes, 80 bytes * 6 * 24 * 365 = 4.2MB per year. In 2008, computers were mainly sold with 2GB of RAM, and Moore’s law predicts that this value will increase by 1.2GB per year, therefore disk space should not be a problem, even if block headers are stored in memory.
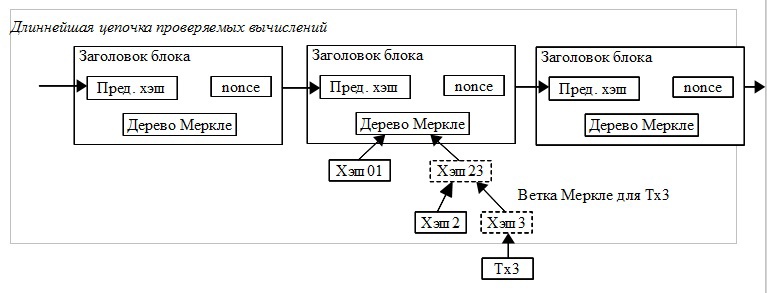
The site has the ability to check payments even if there is no information about the entire network. It is enough for the user to have a copy of the block headers of the longest chain, which he can receive by polling the network nodes until he decides that he has received the longest chain. After that, the user gets the Merkle branch, associating the transaction with a block with the same timestamp as the transaction. He cannot verify the transaction itself, but by comparing it with a place in the chain, he can see that the node has accepted it, and the blocks added after confirm that the network has accepted this transaction.
Of course, such a check is possible when most of the nodes in the network are honest, but it is vulnerable if the network is controlled by an attacker. Although network nodes can verify each other’s transactions, a simplified method can be used by attackers for false transactions if the attackers control the network. One method of protection against this may be the processing of messages from hosts when they detect the wrong block. A user program, upon receiving a message, can download the entire block and a suspicious transaction in order to check it in the usual way. For a business in which payments come often, the best solution would be to have a full-fledged network node for a safer and faster verification of transactions.
Although it is possible to transfer coins separately, it may be too cumbersome to make a separate transaction for each cent transferred. In order to be able to divide and combine amounts, transactions contain multiple inputs and outputs. Usually they have either one input from a large previous transaction, or a set of inputs combining small amounts, as well as at least two outputs: one for payment and one for returning the change, if any, back to the sender.
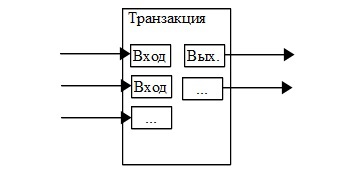
It should be noted that such a fan of transactions dependent on several transactions, which depend on several more, is not a problem here, because there is never any need to restore the history of all transactions.
In the traditional banking model, confidentiality is achieved by restricting access to information by all parties involved. The need to publicly announce all transactions eliminates this approach, but confidentiality can still be maintained due to the anonymity of public keys. Everyone can see that someone has transferred a certain amount to someone, but this information cannot be compared with a specific person. This is like stock trading, where the time and size of transactions are known to everyone, but the parties to the transaction are not disclosed.
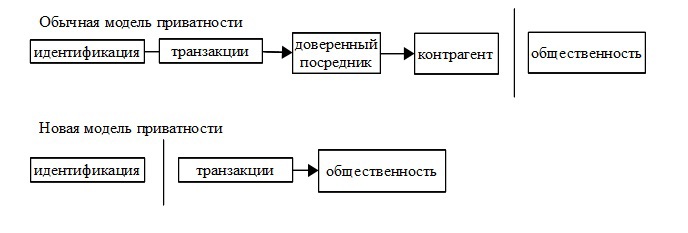
As an additional security screen, for each transaction a new key pair must be used that cannot be matched with the common owner. Some comparisons are still unavoidable in transactions with many entries, since all entries are considered to belong to the same owner. The risk is that if the owner of the key is identified, it will be possible to find out other transactions of this owner.
Consider a scenario where an attacker tries to generate an alternative chain faster than honest nodes. Even if he succeeds, he will not be able to make any changes in the system, for example, to create coins from the air or take coins that no one has transferred to him. Nodes will not accept an incorrect transaction as a payment, and honest nodes will never accept a block with an incorrect transaction. An attacker can only change one of his own transactions by returning to himself the payment he recently made.
The race between the fair chain and the attacker's chain can be described in terms of Binomial Random Walk. A successful event is an increase in the fair chain by one block with an approach to the goal by +1, an unsuccessful event is an increase by one block in the attacker's chain with a decrease in the gap by -1.
The possibilities of an attacker in a race in the face of constraints are similar to the description of the Gambler's Ruin problem. Suppose a gambler with an unlimited credit starts the game under conditions of restriction and can potentially hold an unlimited number of games to try to achieve break-even. We can calculate the likelihood of them achieving a break-even, or that the attacker will overtake honest chain builders.
p = probability that an honest host will find the next block
q = probability that the attacker will find the next block
q z = probability that the attacker will win the race if he is lagging behind by z blocks

Suppose that p> q then the probability decreases exponentially with an increase in the number of blocks that the attacker is behind. Thus, if he fails to get ahead at the very beginning, then his chances of winning in the future will become vanishingly small.
Consider now how long the payee must wait to be sure that the sender will not be able to change the transaction. Suppose that the sender is an attacker who wants the recipient to believe that the payment has been made, but after a while to return the payment to himself. The recipient will be notified when this happens, but the sender hopes that it will be too late.
The recipient generates a new key pair and gives the public key to the sender shortly after its signature. This does not allow the sender to prepare a block chain in advance working on it ahead of time to complete the transaction at the moment. Only when a transaction is sent, can a dishonest sender begin to work in secret on a parallel chain containing an alternative version of this transaction.
The recipient waits for the transaction to be added to the block and Z blocks will be added after that. He does not know at what stage of construction the attacker is, but assuming that honest blocks were built with the same average time per block, the expected value of the attacker's progress can be found through the Poisson distribution:
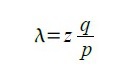
To obtain the probability with which the attacker can still come forward, multiply the Poisson distribution of each value of the attacker's progress by the probability that he will come forward from this point:
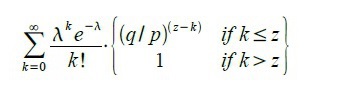
Or after regrouping:
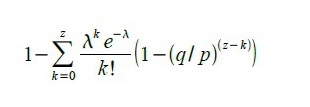
Convert with C code:
By running this program, it is easy to verify that the probability decreases exponentially with increasing z:
q = 0.1
z = 0 P = 1.0000000
z = 1 P = 0.2045873
z = 2 P = 0.0509779
z = 3 P = 0.0131722
z = 4 P = 0.0034552
z = 5 P = 0.0009137
z = 6 P = 0.0002428
z = 7 P = 0.0000647
z = 8 P = 0.0000173
z = 9 P = 0.0000046
z = 10 P = 0.0000012
q = 0.3
z = 0 P = 1.0000000
z = 5 P = 0.1773523
z = 10 P = 0.0416605
z = 15 P = 0.0101008
z = 20 P = 0.0024804
z = 25 P = 0.0006132
z = 30 P = 0.0001522
z = 35 P = 0.0000379
z = 40 P = 0.0000095
z = 45 P = 0.0000024
z = 50 P = 0.0000006
Solutions for P <0.001
P <0.001
q = 0.10 z = 5
q = 0.15 z = 8
q = 0.20 z = 11
q = 0.25 z = 15
q = 0.30 z = 24
q = 0.35 z = 41
q = 0.40 z = 89
q = 0.45 z = 340
We have proposed a system of electronic payments without trusted intermediaries. It is based on the principle of using coins consisting of digital signatures, which provide reliable control on their own, but cannot prevent the problem of dual use. The solution is to use a decentralized network that uses complex calculations to record a public transaction history, which quickly becomes inaccessible for modification by attacking if fair nodes control a large proportion of computational power. Reliability of the network in its unstructured and simple. Each node works independently with minimal coordination. Nodes do not need to identify themselves, since messages go not along a specific route, but along the fastest path. Nodes can leave the network and rejoin, accepting the chain created in the intervening past to check for new transactions. Nodes vote with their computational time, expressing their agreement with the correctness of blocks by attaching them to their chain for further work or ignoring incorrect blocks. With such a mechanism of agreement, you can implement any necessary rules and incentives.
From the translator:
I am not a professional translator and I don’t understand cryptography, but recently I became interested in Bitcoin technology and wanted to start learning from first principles. A quick search on the Internet did not give me a translation of the main article of Satoshi Nakamoto and I decided to try to translate it myself.
Shortly after the translation was started, I realized that English is probably not native to the author of the article, since sometimes it was extremely difficult to understand what the author means and why there are so many “and” particles in one sentence. However, most of the difficulties were overcome and I decided to present this final product to the public.
Short.
Fully decentralized version of electronic payments
will allow online payments directly without financial
organizations. Digital signature is only part of the solution
from which is lost due to the fact that you still need a confidential
a center so that you cannot spend the same money
several times (reuse problem). we
offer a solution to reusable problem with
using technology decentralized networks. By this decision
is sending transactions (along with a network timestamp) to
form of hard-to-calculate hash chains that form a record, which
Cannot be changed without computing the hash chain. The longest
the chain is the most reliable evidence
sequence of events due to the fact that its creation
spent the most computing power. Insofar as
primary computing power controlled by nodes
networks not affiliated with intruders, these nodes will be
generate chains faster and longer than attackers. Herself
the network itself requires a minimal structure. For the best
performance, messages are being broadcast,
nodes can leave the network and join again, accepting and
writing down the longest generated hash chains
during the absence of a node.
')
1. Introduction
Electronic payments on the Internet are almost entirely dependent on financial institutions that are a trusted third party to make a payment. Although the system works well for most transactions, it suffers from a congenital defect: a model based on trust.
Completely non-refundable payments are impossible, since financial institutions cannot avoid disputes with intermediaries. Costs associated with intermediaries increase transaction costs, which leads to the limitation of the minimum transaction size and makes it impractical to make small daily payments. In addition, the price increases due to the impossibility of making non-refundable payments for services that provide non-refundable services. The ability to return requires trusted intermediaries. Sellers are forced to beware of their customers, requiring more information from them than would be required if the possibility of non-refundable payments is possible. A certain percentage of returns is assumed as inevitable. These costs and doubts can be avoided if the buyer uses ordinary money, but there is no mechanism for making payments on the Internet without an intermediary that is trusted.
That is why an electronic payment system is needed, based on cryptographic complexity instead of trust, allowing any two parties to make transfers to each other without trust brokers. Transactions that are almost impossible to undo will protect sellers from fraudsters, and the routine escrow mechanisms can be easily implemented to protect customers. In this article, we propose a solution to the problem of reusable funds using a distributed timestamp server that generates complex-calculated transactions in chronological order. The system is safe as long as the friendly nodes simultaneously control more computing power than any group of attackers.
2. Transactions
The chain of digital signatures will be called electronic coins. Each owner sends the coins to the next one, adding a digitally signed hash of the previous transaction and its public key to the end of the chain. The payee can verify the signature (coin) by checking the chain of owners.
From translator
In the original . For three days I tried to correlate what was written with the one below, until I came across an article: habrahabr.ru/post/114642 Only then I realized that the “next owner” is not “the next owner in relation to the current one”, but “the next one in relation to previous, that is, the current. "

The problem, of course, is that the payee cannot find out if someone from the previous owners had spent the same money twice. Usually this problem is solved by using a trusted centralized intermediary organization that checks each transaction for double spending. After each transaction, the coin must return to the intermediary who, instead of the old one, issues a new coin, then only coins issued by the intermediary are guaranteed not to be spent twice.
The problem with this approach is that the fate of the entire financial system depends on the intermediary company, since all transactions go through it like a bank.
So, you need a way by which the recipient will know that the senders have not paid the same coins with someone else. In our case, only the previous transaction history is important; subsequent attempts to double-use coins do not bother us. The only way to confirm the absence of a transaction is to know all the transactions. In the intermediary model, the intermediary is aware of all transactions and their sequence. To achieve this without a trusted intermediary, all transactions must be known to everyone, i.e. need a system whose members will agree on a single history of all payments. Payment recipients need to verify that during the transaction most participants agree that it was received for the first time.
3. Timestamp server
The solution we offer is based on a timestamp server. The job of the timestamp server is to hash a block of records, memorize time and publish a hash. The time stamp is evidence that the data existed at that time and in the order in which they arrived for hashing. Each timestamp includes the previous timestamp in its hash forming a chain, in which each successive timestamp confirms the previous one.

4. Complicated calculations.
To implement a timestamp server based on a decentralized network, you need to use an algorithm for complex calculations such as Hashcash. Complicated calculations involve finding the value that, when SHA-256 hashes, will give a hash that will start with a large number of zero bits. The average computation time grows exponentially with the number of zero bits, and the result can be verified by calculating a single hash.
For our timestamp server, we implement complex calculations by increasing the special variable (nonce) inside the block by one, until a hash with the required number of zero bits is found. As soon as time is spent for performing complex calculations, the block cannot be changed without doing the calculation again. Since the following blocks form a chain, the work for changing the block includes the work for changing all the following blocks after it.

Checked complex calculations also solve the problem of obtaining confirmation from the majority of participants. A confirmation based on the principle of “one IP address - one vote” can be discredited by anyone who has a lot of IP addresses under control. Checked calculations are essentially "one processor - one vote." Confirmation from the majority is the longest chain, the creation of which was spent the most amount of computing power. If the core computing power is controlled by honest participants, an honest chain will grow faster than any chain of malicious participants. To modify any block, the attacker will have to do the complex calculations associated with this block, as well as all the blocks after it, will need to catch up and overtake honest block builders. We will show further that in a slow attacker, the ability to catch up exponentially decreases with the addition of new blocks.
5. Network
The following steps describe the network operation:
1) A new transaction is broadcast to all nodes.
2) Each node places new transactions in a block.
3) Each node performs complex calculations to find its block
4) When a node finds a solution for its block, it broadcasts this block to all nodes.
5) A node accepts a block only if all transactions in it are correct and not expired.
6) Consent node to accept the block is expressed in the fact that the node begins work on creating the next block in the chain, using the hash of the received block as the previous hash.
Nodes always perceive the longest chain as correct and work on increasing it. If two nodes simultaneously broadcast different versions of the next block, the nodes may receive each of the versions at different times. In this case, the node starts working with the block that was received earlier, but another version should be saved in case it subsequently becomes a longer chain. Branches can be ignored when the next stage of calculations is completed and one of the branches becomes longer than the others; nodes working with other branches will switch to the longest.
Broadcast sending a new transaction does not have to reach all nodes. It will be included in the block as soon as it reaches many nodes. Broadcast parcel blocks, too, may not reach all. If the node has not received a block, it will request it when it receives the next block to fill in the missing links of the chain.
6. Stimulus
We agree that the first transaction in the block will be a special transaction that starts a new coin belonging to the creator of the block. This will add an incentive for the nodes to maintain the network and provide a way to initially put coins into circulation, since there is no central authority for their release. The constant addition of new coins is like mining, when resources are spent to add gold to circulation. In our case, CPU time and electricity are consumed.
Stimulus may also be present when transactions are being carried out. If the value at the output of the transaction is less than the value at the input, this difference is added to the stimulus value of the block containing the transaction. When a predetermined number of coins is issued, the stimulation will be made only through transactions, i.e. inflation will completely disappear.
Stimulus encourages nodes to stay honest. If a greedy attacker can gather more computing power than all honest nodes, then he will have to make a choice: to deceive people by stealing their coins or by generating new coins themselves. He will find it more profitable to play by the rules, the rules that will allow him to get more coins than any other combinations and not to undermine the system, and with it his own state.
7. Disk Space Usage
While the last transactions are written to the block, the declined transactions also take up disk space. To fix this without changing block hashes, transactions are hashed into the Merkle Tree, where only the root is included in the block hash. Old blocks can be packed by trimming tree branches. Internal hashes can not be saved.

The block header without transactions takes approximately 80 bytes. If blocks are generated every 10 minutes, 80 bytes * 6 * 24 * 365 = 4.2MB per year. In 2008, computers were mainly sold with 2GB of RAM, and Moore’s law predicts that this value will increase by 1.2GB per year, therefore disk space should not be a problem, even if block headers are stored in memory.
8. Simplified payment verification
The site has the ability to check payments even if there is no information about the entire network. It is enough for the user to have a copy of the block headers of the longest chain, which he can receive by polling the network nodes until he decides that he has received the longest chain. After that, the user gets the Merkle branch, associating the transaction with a block with the same timestamp as the transaction. He cannot verify the transaction itself, but by comparing it with a place in the chain, he can see that the node has accepted it, and the blocks added after confirm that the network has accepted this transaction.

Of course, such a check is possible when most of the nodes in the network are honest, but it is vulnerable if the network is controlled by an attacker. Although network nodes can verify each other’s transactions, a simplified method can be used by attackers for false transactions if the attackers control the network. One method of protection against this may be the processing of messages from hosts when they detect the wrong block. A user program, upon receiving a message, can download the entire block and a suspicious transaction in order to check it in the usual way. For a business in which payments come often, the best solution would be to have a full-fledged network node for a safer and faster verification of transactions.
9. Combining and splitting the amount
Although it is possible to transfer coins separately, it may be too cumbersome to make a separate transaction for each cent transferred. In order to be able to divide and combine amounts, transactions contain multiple inputs and outputs. Usually they have either one input from a large previous transaction, or a set of inputs combining small amounts, as well as at least two outputs: one for payment and one for returning the change, if any, back to the sender.

It should be noted that such a fan of transactions dependent on several transactions, which depend on several more, is not a problem here, because there is never any need to restore the history of all transactions.
10. Confidentiality
In the traditional banking model, confidentiality is achieved by restricting access to information by all parties involved. The need to publicly announce all transactions eliminates this approach, but confidentiality can still be maintained due to the anonymity of public keys. Everyone can see that someone has transferred a certain amount to someone, but this information cannot be compared with a specific person. This is like stock trading, where the time and size of transactions are known to everyone, but the parties to the transaction are not disclosed.

As an additional security screen, for each transaction a new key pair must be used that cannot be matched with the common owner. Some comparisons are still unavoidable in transactions with many entries, since all entries are considered to belong to the same owner. The risk is that if the owner of the key is identified, it will be possible to find out other transactions of this owner.
11. Calculations
Consider a scenario where an attacker tries to generate an alternative chain faster than honest nodes. Even if he succeeds, he will not be able to make any changes in the system, for example, to create coins from the air or take coins that no one has transferred to him. Nodes will not accept an incorrect transaction as a payment, and honest nodes will never accept a block with an incorrect transaction. An attacker can only change one of his own transactions by returning to himself the payment he recently made.
The race between the fair chain and the attacker's chain can be described in terms of Binomial Random Walk. A successful event is an increase in the fair chain by one block with an approach to the goal by +1, an unsuccessful event is an increase by one block in the attacker's chain with a decrease in the gap by -1.
The possibilities of an attacker in a race in the face of constraints are similar to the description of the Gambler's Ruin problem. Suppose a gambler with an unlimited credit starts the game under conditions of restriction and can potentially hold an unlimited number of games to try to achieve break-even. We can calculate the likelihood of them achieving a break-even, or that the attacker will overtake honest chain builders.
p = probability that an honest host will find the next block
q = probability that the attacker will find the next block
q z = probability that the attacker will win the race if he is lagging behind by z blocks

Suppose that p> q then the probability decreases exponentially with an increase in the number of blocks that the attacker is behind. Thus, if he fails to get ahead at the very beginning, then his chances of winning in the future will become vanishingly small.
Consider now how long the payee must wait to be sure that the sender will not be able to change the transaction. Suppose that the sender is an attacker who wants the recipient to believe that the payment has been made, but after a while to return the payment to himself. The recipient will be notified when this happens, but the sender hopes that it will be too late.
The recipient generates a new key pair and gives the public key to the sender shortly after its signature. This does not allow the sender to prepare a block chain in advance working on it ahead of time to complete the transaction at the moment. Only when a transaction is sent, can a dishonest sender begin to work in secret on a parallel chain containing an alternative version of this transaction.
The recipient waits for the transaction to be added to the block and Z blocks will be added after that. He does not know at what stage of construction the attacker is, but assuming that honest blocks were built with the same average time per block, the expected value of the attacker's progress can be found through the Poisson distribution:
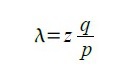
To obtain the probability with which the attacker can still come forward, multiply the Poisson distribution of each value of the attacker's progress by the probability that he will come forward from this point:
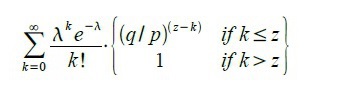
Or after regrouping:
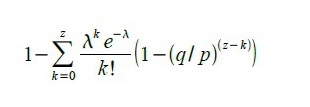
Convert with C code:
#include <math.h> double AttackerSuccessProbability(double q, int z) { double p = 1.0 - q; double lambda = z * (q / p); double sum = 1.0; int i, k; for (k = 0; k <= z; k++) { double poisson = exp(-lambda); for (i = 1; i <= k; i++) poisson *= lambda / i; sum -= poisson * (1 - pow(q / p, z - k)); } return sum; } By running this program, it is easy to verify that the probability decreases exponentially with increasing z:
q = 0.1
z = 0 P = 1.0000000
z = 1 P = 0.2045873
z = 2 P = 0.0509779
z = 3 P = 0.0131722
z = 4 P = 0.0034552
z = 5 P = 0.0009137
z = 6 P = 0.0002428
z = 7 P = 0.0000647
z = 8 P = 0.0000173
z = 9 P = 0.0000046
z = 10 P = 0.0000012
q = 0.3
z = 0 P = 1.0000000
z = 5 P = 0.1773523
z = 10 P = 0.0416605
z = 15 P = 0.0101008
z = 20 P = 0.0024804
z = 25 P = 0.0006132
z = 30 P = 0.0001522
z = 35 P = 0.0000379
z = 40 P = 0.0000095
z = 45 P = 0.0000024
z = 50 P = 0.0000006
Solutions for P <0.001
P <0.001
q = 0.10 z = 5
q = 0.15 z = 8
q = 0.20 z = 11
q = 0.25 z = 15
q = 0.30 z = 24
q = 0.35 z = 41
q = 0.40 z = 89
q = 0.45 z = 340
12. Conclusion
We have proposed a system of electronic payments without trusted intermediaries. It is based on the principle of using coins consisting of digital signatures, which provide reliable control on their own, but cannot prevent the problem of dual use. The solution is to use a decentralized network that uses complex calculations to record a public transaction history, which quickly becomes inaccessible for modification by attacking if fair nodes control a large proportion of computational power. Reliability of the network in its unstructured and simple. Each node works independently with minimal coordination. Nodes do not need to identify themselves, since messages go not along a specific route, but along the fastest path. Nodes can leave the network and rejoin, accepting the chain created in the intervening past to check for new transactions. Nodes vote with their computational time, expressing their agreement with the correctness of blocks by attaching them to their chain for further work or ignoring incorrect blocks. With such a mechanism of agreement, you can implement any necessary rules and incentives.
Source: https://habr.com/ru/post/215557/
All Articles