Differential Cryptanalysis for Dummies

The FEAL code has the same level of durability as DES. Moreover, the increased key length (64 bits compared to 56 bits in DES) makes it difficult to iterate. The code number FEAL has a good distribution of ciphertexts, close to random. And this also speaks in favor of FEAL compared to DES.

This is a summary of the FEAL encryption algorithm specification published in 1987.

Nothing is eternal under the Moon. In this topic, I will tell you how, with only 40 pairs of open-closed texts, get the full key of FEAL4 in a few minutes.

Differential Cryptanalysis

To begin with, let’s see what is hidden under the name “Differential cryptanalysis” that caresses the Russian ear.
Differential cryptanalysis is an attack with selected plaintext. This means that in order to use DK, you must be able to encrypt absolutely any text in absolutely any quantity.
')
The goal of an attacker using DCs is to get some information about the key, which can completely compromise the key (which is very rare) and simply give some advantage when selecting the key.

It all works as follows. For two pre-selected ciphertexts P ₁ and P _{2, the} attacker calculates the “differential” ΔP = P ₁ ⊕P ₂ . And using ΔP, it tries to determine what the “differential” of ciphertexts should be ΔC = C ₁ C ₂ . It is often impossible to predict with 100% accuracy what exactly will be the value of ΔC. The only thing an attacker can do is determine at what frequency the cipher returns different ΔC values, for a predetermined ΔP. This knowledge allows an attacker to open part of the key or the entire key.

As an example, consider the three-round block cipher shown in the figure below.

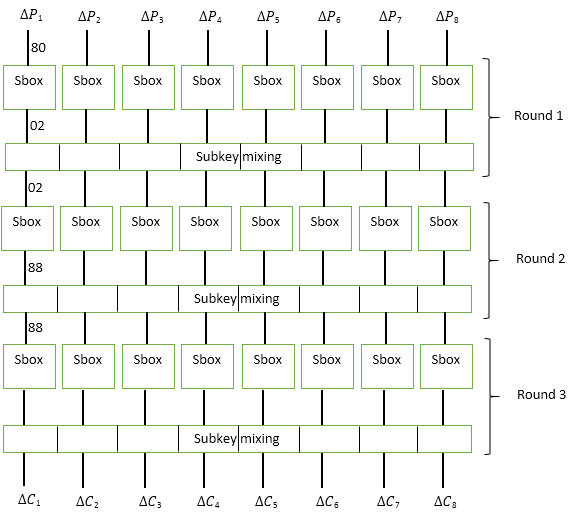
This cipher has 64 bit block size and 128 bit key.
At each round, the input block is divided into 8 bytes, each of which passes through the Sbox substitution function . After that, the data is mixed with a Subkey 64-bit subkey. The mixing function is a regular XOR.

Suppose that the attacker decided to check the differential 0x80. To do this, it generates an arbitrary byte X ₁ , and calculates X ₂ = X ₁ ⊕80.
Next, the attacker drives X ₁ and X ₂ through the Sbox function and gets the values ​​of Y ₁ and Y ₂ . For each such pair of X ₁ and X ₂ , the differential of which is 80, the attacker is able to get the differential ΔY. Analyzing the values ​​obtained, the attacker chooses a value of ΔY, which has a greater probability of occurrence.

Returning to our example, suppose that of all 256 pairs of X ₁ and X ₂ , in 192 cases Y ₁ ⊕ Y ₂ = 02. Thus, the probability that for a given ΔX = 80, the value of ΔY = 02, is 192/256 = 3/4. This in turn means that for a given ΔX = 80, with a probability P ₁ = 3/4, two values ​​of U ₁ and U ₂ will fall into the input of the second round, such that ΔU = 02.
Note that the key does not in any way affect the value of the differentials. Since when encrypting different texts, the key does not change and mixing with the key sequence is performed using XOR, when calculating ΔU, the key bytes are mutually exclusive.

To reveal the properties of the second round, the attacker generates new 256 pairs of input bytes X ₁ and X ₂ , such that X ₁ ⊕ X ₂ = 02. Having calculated the Sbox function for each pair of X ₁ and X ₂ , the attacker notices that in 64 cases out of 256 ΔY = 88. Those. the probability that ΔY = 88, for a given ΔX = 02, is P ₂ = 64/256 = 1/4.

Thus, having performed a simple calculation of probabilities, the attacker understands that for the specified cipher for each pair of bytes X ₁ and X ₂ , such that ΔX = 80, with probability P = P ₁ * P ₂ = 3/4 * 1/4 = 3 / 16, the differential of the internal state of the cipher before the last round is ΔY = 88.

With this knowledge, the attacker generates several pairs of texts such that ΔP = 808080808080 and proceeds to a byte selection of the subkey of the third round.
Let us show how the first byte of the subkey is opened.
For each of the 256 possible variants of the first byte of Subkey [0] and for each pair of ciphertexts {C ₁ , C ₂ }, the attacker calculates U ₁ = Sbox (C ₁ ⊕Subkey [0]) and U ₂ = Sbox (C ₂ ⊕Subkey [0]).
If Subkey [0] is correctly guessed, then approximately 3 out of every 16 pairs of U ₁ and U ₂ will be 88 when calculating ΔU.
Having picked up the most probable first byte of the Subkey subkey in this way, an attacker can go to the second byte and, in a similar way, open the entire key of the third round.

After the key of the last round is revealed, the attacker can launch an attack on the penultimate round and, acting in this way, will eventually receive information on all the round cipher keys.

FEAL cipher description

Now consider the cryptoalgorithm with which we will try to perform the actions described above.
So, FEAL4 is a block cipher, with a block size and key length equal to 64 bits.
There are several equivalent descriptions of the FEAL4 algorithm; we will use the most convenient for demonstrating differential cryptanalysis.

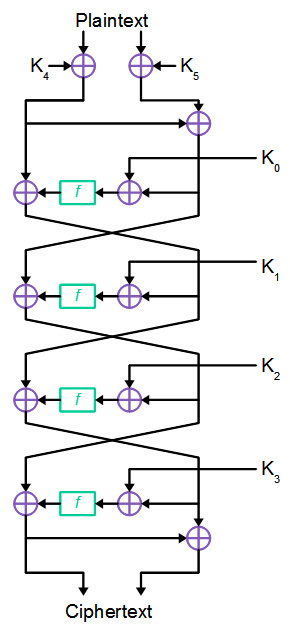
The cipher consists of 4 rounds and uses six 32-bit subkeys generated from the primary key (hereafter, we assume that each subkey is generated independently, thus increasing the threshold in such a way from 2 ⁶⁴ to 2 ¹⁹² ).

At the initial stage, the plaintext is divided into two blocks, 32 bits each. The left and right blocks are folded modulo two with 32-bit subkeys K [4] and K [5], respectively. Then the left part remains unchanged, and the right is formed by adding modulo two with the left block.

After that, 4 rounds of encryption are performed on each of which the right block is modulo-2 summed up with the subkey of the round K [i], and then the result is run through the permutation function F. The result of the permutation is added to the left part of the text. After these operations, the left and right blocks are reversed and the result is fed to the input of the next round.

The last round is a bit different from everyone else. Left and right blocks do not change places, as in previous rounds.
Instead, the right block is folded modulo two with the left block and the result is returned as the right side of the ciphertext. The left part after the 4th round remains unchanged and makes up the first 32 bits of the received ciphertext.

The original cipher scheme described by the creators was somewhat different from the one above. Instead of six 32-bit, the original description uses twelve 16-bit subkeys. However, both options are identical and, if desired, 32-bit keys can be easily represented as 16-bit keys from the original description.



The only white spot in the cipher description is function F. It can be represented in the figure as follows:


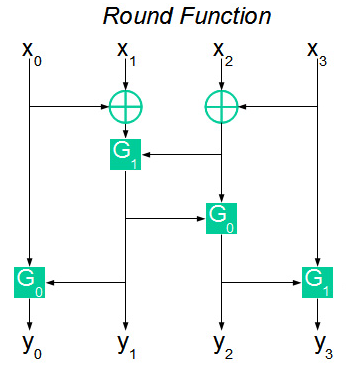
At the input, the F function gets 4 bytes X ₁ , X ₂ , X ₃ , X ₄ . Next, the input bytes are mixed and pass through the functions G ₀ or G ₁ . The 4 bytes received after calculating the functions G _x form the 32-bit output sequence of the function F.

The G ₀ and G ₁ functions convert the 16-bit input sequence to an 8-bit result.
The function G ₀ can be expressed as follows: 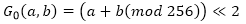where << is a cyclical shift to the left.
While the function G ₁ has the following definition: .

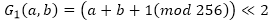Decryption of the algorithm occurs on the same principle. Actually, the ciphertext is divided into left and right blocks and all encryption operations are performed in the reverse order.
Those. first decryption of the last round, then the last but one, and so on.

Differential cryptanalysis of FEAL4 cipher

As in the example above, we begin the cryptoanalysis of the cipher with an examination of the substitution function F. This is where the most significant flaw of the entire FEAL cipher is hidden. The point is that the function F has one property that is catastrophic from the point of view of safety. Any two values ​​of X ₁ and X ₂ , such that their differential X ₁ ⊕ X ₂ = 0x80800000, are converted to Y ₁ and Y ₂ . Moreover, the differential Y ₁ ⊕ Y ₂ = 0x02000000 in 100% of cases.

In order to understand why this happens, take a look at the transformation of the differentials that occurs when calculating the function F.

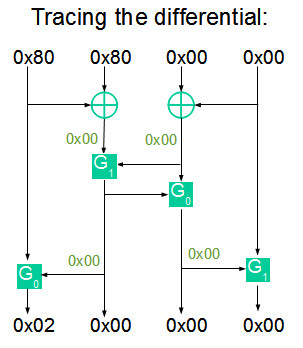
It is easy to see that a nonzero value is fed to the input of the function G, only at the position of the first byte. Accordingly, at the output we get .

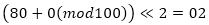It is easy to understand that this property makes the cipher completely vulnerable to differential cryptoanalysis. 100% probability of a certain differential ΔY allows you to reduce the number of pairs of open-closed text required for an attack to a minimum.

Consider what steps an attacker should take to unlock the key of the last round K [3].
The attacker generates several pairs of open texts P ₁ and P ₂ , such that ΔP = 0x8080000080800000. Knowing the property of the function F described above, an attacker is able to calculate the differentials at almost every encryption round.

You can track the behavior of differentials in the following picture:

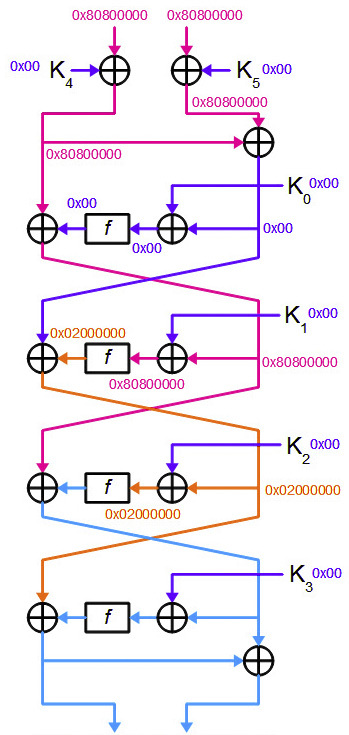
As you can see the differentials are calculated until the last round. But even without this, the attacker already has enough information to reveal the last round key.
The illustration below shows the last two rounds of the FEAL4 cipher.

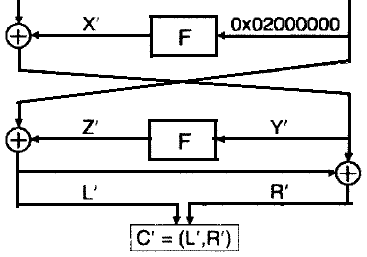
Possessing a pair of C ₁ and C ₂ ciphertexts, an attacker can calculate ΔC, thus obtaining the values ​​of L 'and R'.
Based on this, he can calculate Z '= L'⊕02.
On the other hand, for each pair of C ₁ and C ₂ ciphertexts, an attacker can calculate Y ₁ and Y ₂ .
Knowing Y ₁ and Y _{2, the} attacker starts searching the key K [3]. For each possible Kpos key, Z ₁ = F (Y ₁ ⊕ Kpos) and Z ₂ = F (Y ₂ ⊕ Kpos) are calculated. Adding modulo two values ​​Z ₁ ⊕Z _{2, the} attacker compares the resulting value with the pre-calculated Z '. If Z '= Z ₁ ⊕Z ₂ , then Kpos is most likely the required subkey K [3].
In order to reduce the likelihood of an error, the received Kpos key must be checked with several pairs of ciphertexts (I used 10 pairs in my implementation).

It is easy to calculate that the attack described above requires 2 ³² calculations of the function F. This is certainly not 2 ⁶⁴ , declared by the cipher creators, but still the figure is not very pleasant, especially if we want to calculate all 4 round keys, and we certainly want it.
Fortunately, the attack can be simplified and reduce the number of calculations to a completely comfortable 2 ¹⁷ .
To do this, we introduce the definition of the function 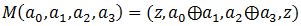where a is a set of bytes, and z is a zero byte.
For each A = (z, a ₀ , a ₁ , z), the attacker calculates Q ₀ = F (M (Y ₀ ) ⊕A) and Q ₁ = F (M (Y ₁ ) ⊕A).
It is easy to verify that if A = M (K [3]), then the second and third byte of the value Q ₀ ⊕Q ₁ will coincide with the second and third byte of the value Z '. Thus, we obtain information on two bytes of the potential key Kpos.
After that, for all values ​​of b ₀ and b ₁ , the attacker calculates the sequence Kpos = (b ₀ , b ₀ ⊕ a ₀ , b ₁ ⊕ a ₁ , b ₁ ) and checks the resulting sequence in the manner described above.

After opening the subkey K [3], the attacker is able to restore the values ​​in which the cipher was located after the third round and this will give him the opportunity to attack the subkey K in the same way [2]. Here, however, it should be noted that in order to attack the key K [2], it will be necessary to use another initial differential, since the differential ΔP = 0x8080000080800000 in the second round always leads to the value Z '= 0x02000000, for any used key. And it does not allow to guess the key of the second round.
The following values ​​can be used as differentials for opening each subkey:
Round 4: 0x8080000080800000
Round 3: 0x0000000080800000
Round 2: 0x0000000002000000
Round 1: 0x0200000080000000
After opening all four keys of each of the rounds, it is easy to calculate the keys K [5] and K [4] for this purpose it is enough to drive out any ciphertext after 4 rounds of decryption and add the resulting value modulo two with known plaintext.

If you are interested in downloading the source of the attack, you can here .

useful links

• Tutorial on Linear and Differential Cryptanalysis
• Differential Cryptanalysis of FEAL