OpenFOAM in practice

Open foam

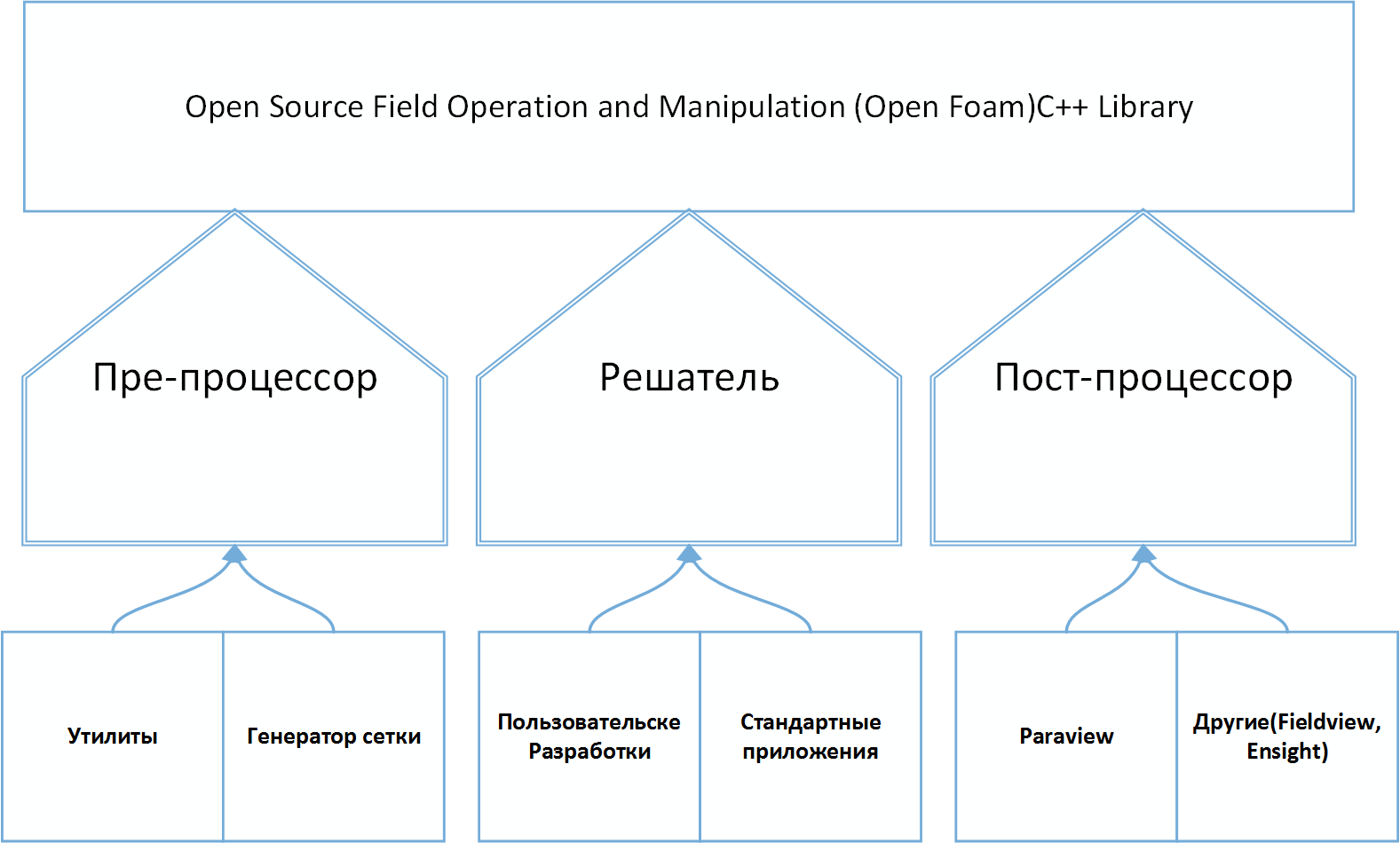
OpenFOAM is a freely available computational fluid dynamics toolkit for operations with fields (scalar, vector and tensor). Today it is one of the “completed” and well-known applications designed for FVM computing. In particular, the package allows us to solve the hydrodynamic problems of Newtonian and non-Newtonian viscous fluids in both incompressible and compressible approximation, taking into account convective heat exchange and gravity. To simulate turbulent flows, it is possible to use RANS models, LES and DNS methods. Perhaps the solution subsonic, transonic and supersonic problems.

The package is based on a set of libraries that provide tools for solving systems of partial differential equations both in space and in time. The working language of the code is OOP C ++. In terms of this language, most mathematical differential and tensor operators in the program code (prior to translation into the executable file) equations can be represented in a readable form, and the discretization and solution method for each operator can be selected by the user during the calculation. Thus, the code completely encapsulates and separates the concepts of the computational grid (discretization method), discretization of the basic equations, and methods for solving algebraic equations.

Task

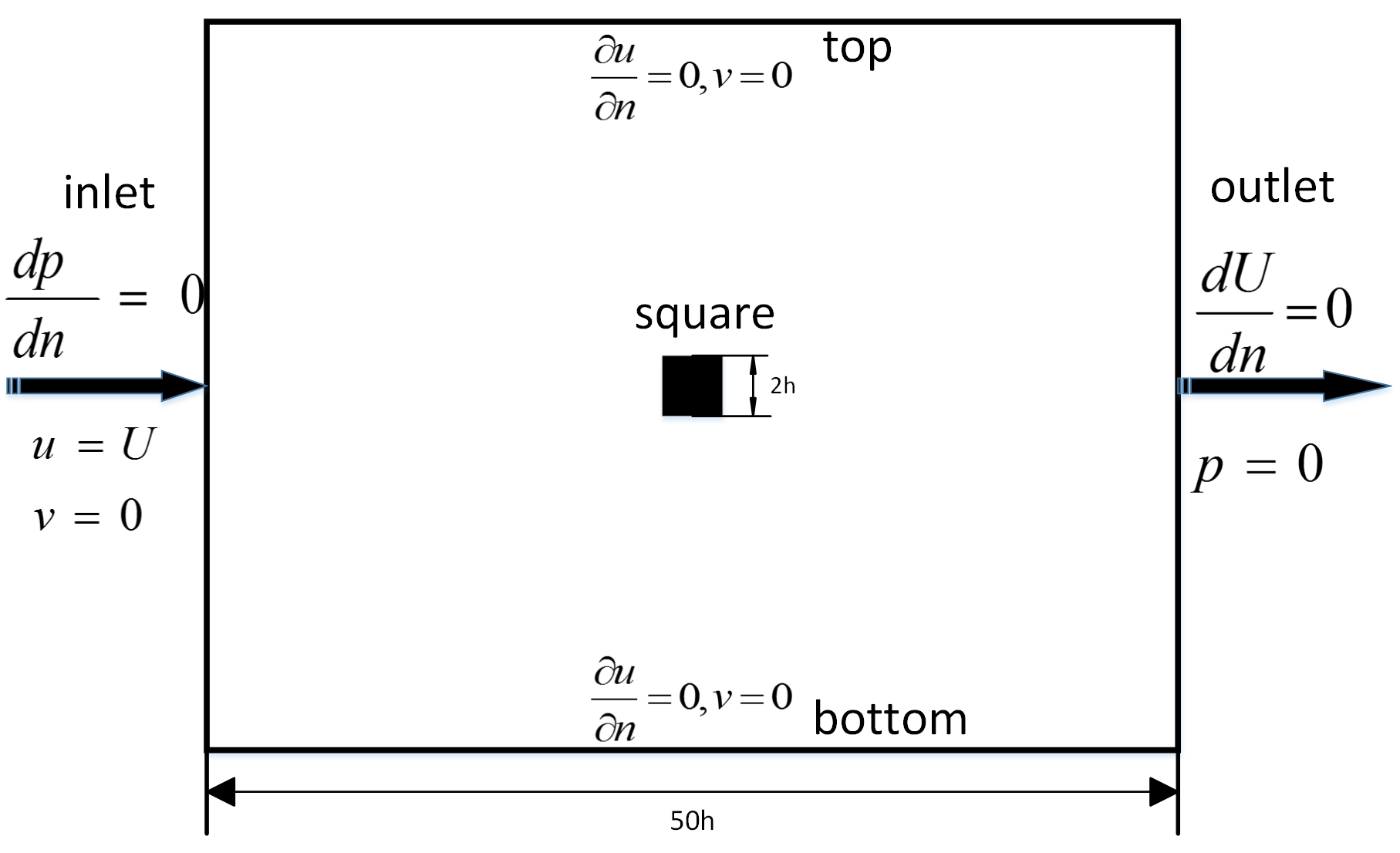
We solve the problem of flow around an infinite square cylinder. Liquid is incompressible and viscous.
For such problems a lot of experimental data. Therefore, in the end we will be able to compare the results of numerical simulation.

Where U = (u, v) is the dimensionless velocity, p is the dimensionless pressure, Re is the Reynolds number .
')
Block grids are used to discretize the computational domain. The construction is done by means of the utility blockmesh, package OpenFOAM. The area is divided into non-intersecting cubic cells. To account for two-dimensionality, special boundary conditions are used on the front "front" and on the rear border of the "back" region parallel to the flow plane.

The border	Variable	Type of boundary conditions
"Front", "back"	U, p	empty
"Inlet", "outlet"	U	Fixedvalue
"Inlet", "outlet"	p	Fixedvalue
"Bottom", "top"	U	ZeroGradient
"Bottom", "top"	p	ZeroGradient
"Square"	U	ZeroGradient
"Square"	p	Fixedvalue

Partitioning scheme

The infinite region is replaced by a bounded region, which is a rectangular parallelepiped, in the center of which is placed a square cylinder. The choice of a three-dimensional solution area is carried out in accordance with the software feature. OpenFOAM does not provide a solution to 2D problems.

Discretization of the system of equations of motion in this OpenFOAM computing package is performed using the Finite-volume method (Finite-volume method) . Localization of discrete values of speed and pressure is performed in the centers of the cells of the constructed computational grid.

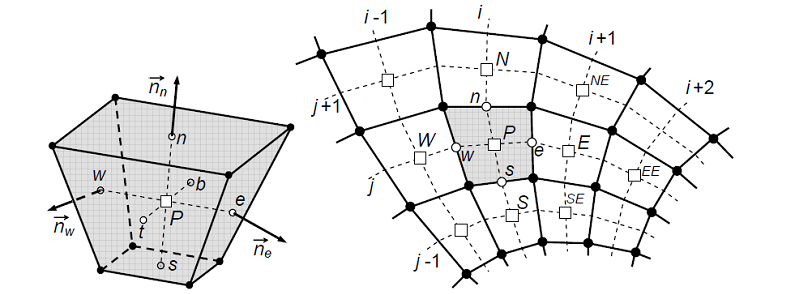
Term	Approximation scheme in the OpenFOAM package	Approximation order
Time derivative	Euler	The first
Pressure gradient	Gauss linear	Second*
Convective term	Gauss limitedCubicV 0.2	First second
Laplacian	Gauss linear corrected	Second*

* - in some areas, mesh characteristics may reduce the order of accuracy.

Decision

The task is solved using the icoFoam utility based on the PISO algorithm. The main steps are shown in the diagram. The iterative procedure is based on the sequential solution of equations for velocity and pressure.

To solve the system of linear equations for p, the PCG solver (pre-adjoint gradients) was used. To set the initial approximation, the GAMG solver ( multigrid method with V cycle ) was used, with Gauss-Seidel smoothing. To solve the system of linear equations for U, the PBiCG (pre-bis-conjugate gradient) solver was used, with the DILU (Diagonal incomplite-LU) solver for initial approximations.

Task	Solution Method	Options
For pressure	PCG	GAMG preconditioner, tolerance 1e-6; relTol 0;
Preconditioner	Gamg	Smoother GaussSeidel; agglomerator faceAreaPair; mergeLevels 1; relTol 0; nCellsInCoarsestLevel 10; cacheAgglomeration true;
For speeds	Pbicg	solver PbiCG; preconditioner DILU; tolerance 1e-06; relTol 0;

Preconditioner - preconditioner,
Tolerance is the maximum allowed value of the residual modulus,
Smoother - smoothing method
Agglomerator –agglomerator,
nCellsInCoarsestLevel - the number of cells on the coarsest grid.

The domain decomposition method of the computational domain is applied. The solution area is divided into 4 smaller subdomains, which are calculated on different processor cores.

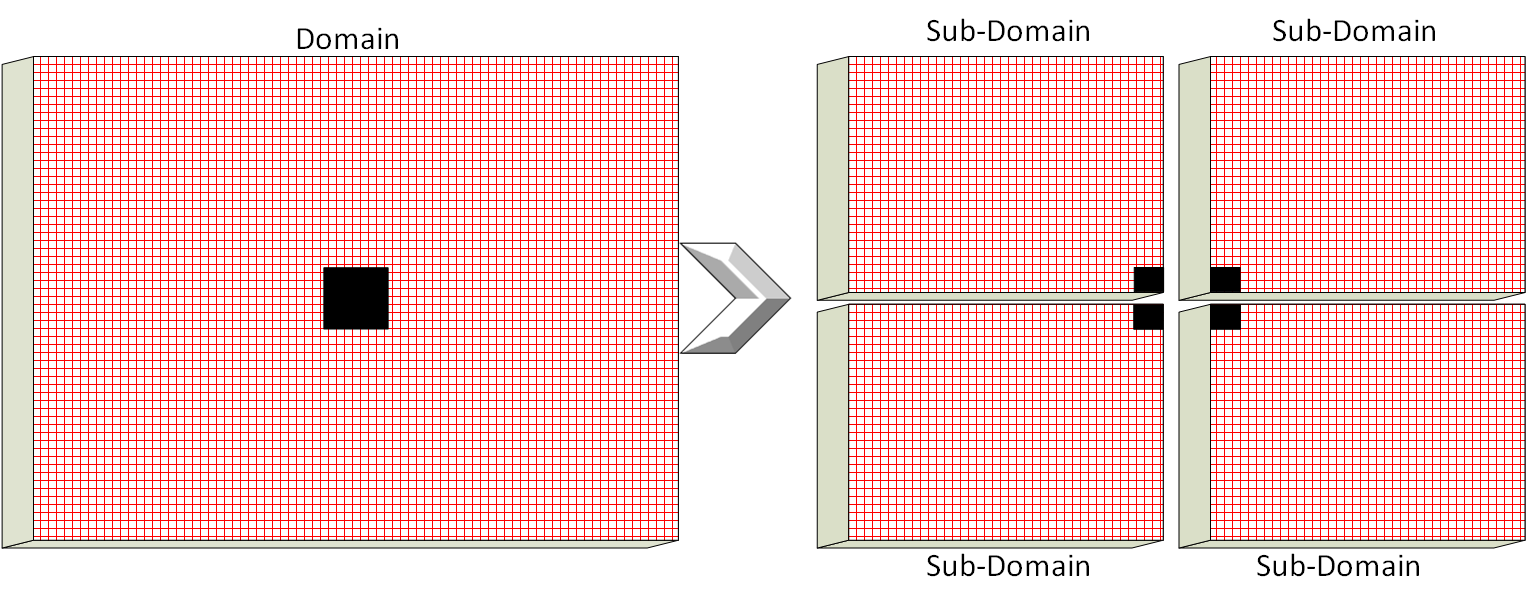
results

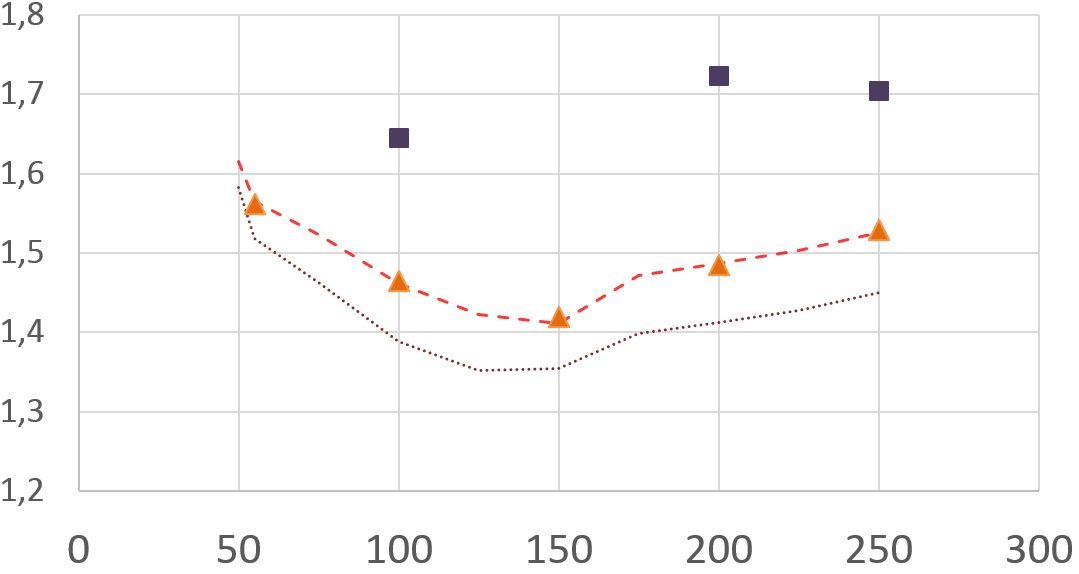
The dependence of Cd on the Reynolds number.

▲ - OpenFOAM, ∎ Davis & Moore (1982) - - - - - Shushant Dutta (2008) Hera (2010)
Our results almost coincided with the results of other researchers. However, for beveled grids, the results are significantly different from the experimental ones.

Well, a beautiful picture of the flow.