On the features of the implementation of prefix entropy coding for large alphabets
I think all the readers of Habr are well known algorithms for entropy compression using prefix codes (algorithms of Shannon-Fano, Huffman, etc.). A feature of these algorithms is the fact that the length of the code of a certain symbol depends on the frequency of this symbol in the encoded message. Accordingly, when decoding a message, it is necessary to have a frequency table. This article is devoted to the study of the little-studied, but important task - the transfer of frequencies of the original alphabet.
In the beginning, let's look at the basic idea underlying the entropy prefix coding. Suppose we have a message consisting of letters of the Russian alphabet, for example, "KUKUSHKAKUKUKONKUKIPILAKAPYUSHN". In this message there are only ten different characters {K, U, W, A, O, N, P, I, L, Yu}, which means that each character can be encoded using four bits.
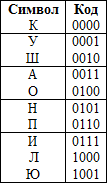
That is, the entire message with such a naive block coding will take 116 bits.
But characters can be assigned to other codes, for example:
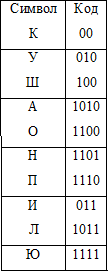
When using codes from Tab. 2 message length is already 90 bits, and the gain is more than 22%. The attentive reader will notice that the codes in Tab. 1 have a constant length, and therefore can be easily decoded. Tab. 2 codes have variable length, but they have another important property - prefix. The prefix property means that no code is the beginning of any other code. For any prefix code, a corresponding tree can be constructed, with the help of which you can uniquely perform decoding of the message:
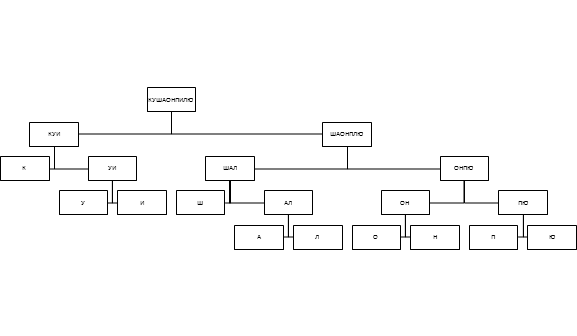
If it is agreed that the zero bit read from the encoded message corresponds to the movement in the tree to the left, and the single bit to the movement to the right, the decoding process becomes obvious.
The question immediately arises whether there is an algorithm for constructing a code tree with minimal redundancy. Huffman, in his work, not only proved that such an algorithm exists, but also proposed it. Since then, the algorithm for constructing a code tree with minimal redundancy is named after it. The basic steps of the Huffman algorithm are listed below:
For our post, the Huffman tree will look like this:
A message encoded using the Huffman algorithm will occupy only 87 bits (a gain of 25% compared to a block code).
In all our calculations, we tacitly implied that during the decoding process the correspondence table symbol-code is known, but in practice this condition is not fulfilled, therefore the table itself is also transmitted along with the encoded message. In most cases, this table is small compared to the size of the encoded message, and the fact of its transmission has little effect on the compression efficiency.
However, sometimes there are situations where the weight of the table becomes significant. For example, in my thesis on lossless video compression, this situation occurs all the time. The power of the alphabet is tens and hundreds of millions of entries.
If you use the traditional approach when a table is passed to an element — the corresponding code — the overhead becomes so large that you can forget about effective compression. The transfer of the form element - the frequency is also not without flaws:
As a result of the research, it was decided to transfer not the entire database, but the elements themselves and a small amount of additional information describing the tree structure. In this case, only two additional bits are additionally transmitted to each base element.
We will agree on the order of bypassing the constructed code tree, for example, we will use a wide bypass. If a dividing tree node is encountered during the walk process, then bit 0 is transmitted, if a leaf was found during the walk process, then bit 1 and k bits are encoded to encode the corresponding base element. As a result, only 2 additional bits are transmitted to each base element.
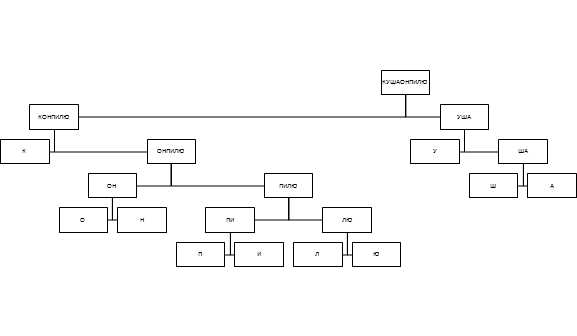
The specified representation is reversible: that is, for each line constructed in the described way, it is possible to build the original code tree. In addition to the obvious memory savings, the proposed transmission method eliminates the need to build a code tree when decoding, thereby significantly increasing the decoding speed. The figure shows the representation of a binary tree as a bit string using the described method:
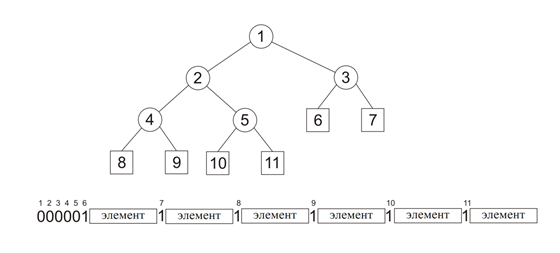
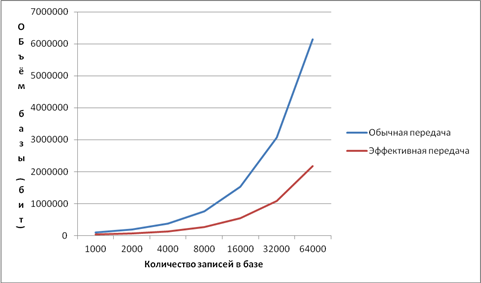
With the encoding method described, the transmission volume is significantly reduced. The figure shows the volume of transmissions when using the described base transfer methods:
But even this method can be significantly improved. When encoding and decoding, it is absolutely not important for us the relative (within the level) location of the nodes, so you can perform the procedure of shuffling the nodes, which consists in moving all the leaves to the left part of the tree, and dividing the nodes to the right. That is, a tree:

Converted to wood

After such a conversion, a single bit means not just a dividing node, but the fact that all the nodes to the left of the processed at this level are also dividing.
Such optimizations may seem insignificant to you, but it is they that have achieved the world's best (in most test video sequences) lossless compression ratio.
PS Even in the case of a fully constructed Huffman tree, the task of obtaining the element code from an elementary in the case of small arrays becomes practically impracticable, which ultimately led to the emergence of a fundamentally new type of binary trees. If it will be interesting to someone, I with pleasure will write one more topic.
PPS I will definitely tell you about the proposed method of video compression, but a little later.
In the beginning, let's look at the basic idea underlying the entropy prefix coding. Suppose we have a message consisting of letters of the Russian alphabet, for example, "KUKUSHKAKUKUKONKUKIPILAKAPYUSHN". In this message there are only ten different characters {K, U, W, A, O, N, P, I, L, Yu}, which means that each character can be encoded using four bits.

That is, the entire message with such a naive block coding will take 116 bits.
But characters can be assigned to other codes, for example:

When using codes from Tab. 2 message length is already 90 bits, and the gain is more than 22%. The attentive reader will notice that the codes in Tab. 1 have a constant length, and therefore can be easily decoded. Tab. 2 codes have variable length, but they have another important property - prefix. The prefix property means that no code is the beginning of any other code. For any prefix code, a corresponding tree can be constructed, with the help of which you can uniquely perform decoding of the message:

If it is agreed that the zero bit read from the encoded message corresponds to the movement in the tree to the left, and the single bit to the movement to the right, the decoding process becomes obvious.
The question immediately arises whether there is an algorithm for constructing a code tree with minimal redundancy. Huffman, in his work, not only proved that such an algorithm exists, but also proposed it. Since then, the algorithm for constructing a code tree with minimal redundancy is named after it. The basic steps of the Huffman algorithm are listed below:
- All symbols of the alphabet are represented as free nodes, with the weight of the node being proportional to the frequency of the symbol in the message;
- From the set of free nodes, two nodes are selected with a minimum weight and a new (parent) node is created with a weight equal to the sum of the weights of the selected nodes;
- The selected nodes are removed from the free list, and the parent node created from them is added to this list;
- Steps 2-3 are repeated as long as there are more than one nodes in the free list;
- Based on the constructed tree, each character of the alphabet is assigned a prefix code.
For our post, the Huffman tree will look like this:

A message encoded using the Huffman algorithm will occupy only 87 bits (a gain of 25% compared to a block code).
In all our calculations, we tacitly implied that during the decoding process the correspondence table symbol-code is known, but in practice this condition is not fulfilled, therefore the table itself is also transmitted along with the encoded message. In most cases, this table is small compared to the size of the encoded message, and the fact of its transmission has little effect on the compression efficiency.
However, sometimes there are situations where the weight of the table becomes significant. For example, in my thesis on lossless video compression, this situation occurs all the time. The power of the alphabet is tens and hundreds of millions of entries.
If you use the traditional approach when a table is passed to an element — the corresponding code — the overhead becomes so large that you can forget about effective compression. The transfer of the form element - the frequency is also not without flaws:
- On the shoulders of the decoder lies the computationally complex task of building a code tree;
- The spread of frequencies is several orders of magnitude, and standard real arithmetic does not always allow one to accurately display it.
As a result of the research, it was decided to transfer not the entire database, but the elements themselves and a small amount of additional information describing the tree structure. In this case, only two additional bits are additionally transmitted to each base element.
We will agree on the order of bypassing the constructed code tree, for example, we will use a wide bypass. If a dividing tree node is encountered during the walk process, then bit 0 is transmitted, if a leaf was found during the walk process, then bit 1 and k bits are encoded to encode the corresponding base element. As a result, only 2 additional bits are transmitted to each base element.
The specified representation is reversible: that is, for each line constructed in the described way, it is possible to build the original code tree. In addition to the obvious memory savings, the proposed transmission method eliminates the need to build a code tree when decoding, thereby significantly increasing the decoding speed. The figure shows the representation of a binary tree as a bit string using the described method:

With the encoding method described, the transmission volume is significantly reduced. The figure shows the volume of transmissions when using the described base transfer methods:

But even this method can be significantly improved. When encoding and decoding, it is absolutely not important for us the relative (within the level) location of the nodes, so you can perform the procedure of shuffling the nodes, which consists in moving all the leaves to the left part of the tree, and dividing the nodes to the right. That is, a tree:

Converted to wood

After such a conversion, a single bit means not just a dividing node, but the fact that all the nodes to the left of the processed at this level are also dividing.
Such optimizations may seem insignificant to you, but it is they that have achieved the world's best (in most test video sequences) lossless compression ratio.
PS Even in the case of a fully constructed Huffman tree, the task of obtaining the element code from an elementary in the case of small arrays becomes practically impracticable, which ultimately led to the emergence of a fundamentally new type of binary trees. If it will be interesting to someone, I with pleasure will write one more topic.
PPS I will definitely tell you about the proposed method of video compression, but a little later.
')
Source: https://habr.com/ru/post/215101/
All Articles