Dykstra from Tim from Stanford
On the beautiful Coursera, the course on Tim from Stanford will soon begin again. And I can't not write about him. And in the light of this post about distance education , all the more so.
To begin with, this is the most interesting course I ever had to take. And I spent in all not the worst universities for many years. The course is called Algorithms: Design and Analysis . It is told in the course about different algorithms for graphs, the appropriate data structures for each algorithm are discussed, there is a theory and brief proofs of these algorithms. The second part describes, among other things, the P = NP problem and algorithms with non-polynomial time.
Why did I like this course so much? Because the lecturer is incredibly cool! He is so involved, he tells it all. And then every week you need to program a new algorithm (in the language of your choice) and find the answer to the question using your implementation. Answer the question on the site, and again, until you get the correct answer. Every week, as I said, a new algorithm. And accordingly deadlines. I was motivated by this simply crazy: I ran home from work and I did not part with the algorithms on weekends, I went on vacation, sat on top of the highest point of the country and programmed sort merge.
')
I waited six months to be announced again its beginning, to advise it to other people, because for me it was like a treasure found.
As an example, here is a picture of how I found the solvability of 2SAT problems with a random algorithm.
2SAT-problem: there is some set of Boolean variables {X1, ..., Xn}, restrictive conditions are given in the form (X1 OR X5), (¬X2 OR X3), (X5 OR X9), ... The task is to determine whether it is possible to satisfy all these conditions at the same time.
The proposed algorithm takes and randomly changes the value of one of the variables in one of the unsatisfied conditions.
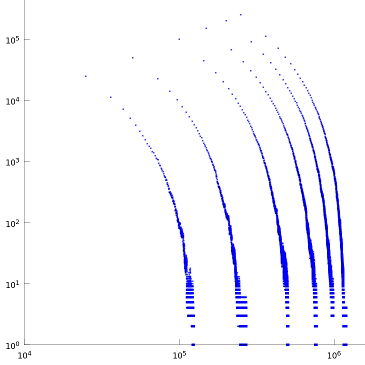
In the picture on the x axis - the number of random coup d'etats (per set run), in y - the number of unsatisfied conditions. 6 different sets of such conditions were given, and it was necessary to determine which of them are solvable (satisfied) and which are not. If the set of conditions is satisfactory, then such a random alteration is a solution. If not, then the number of unsatisfied conditions begins to fluctuate around a certain value. For example, on the second left of the line in the picture, one can see that after some time the system converged to a pair of mutually unsatisfied conditions and these random alterations oscillate the system within several random variations.
Now it seems to me that these were the top 4 months of my life concentrating on interesting things when I was taking this course. And I still think, maybe you will give me advice, in which plan companies and in what positions you need to deal with such things every day.
To begin with, this is the most interesting course I ever had to take. And I spent in all not the worst universities for many years. The course is called Algorithms: Design and Analysis . It is told in the course about different algorithms for graphs, the appropriate data structures for each algorithm are discussed, there is a theory and brief proofs of these algorithms. The second part describes, among other things, the P = NP problem and algorithms with non-polynomial time.
Why did I like this course so much? Because the lecturer is incredibly cool! He is so involved, he tells it all. And then every week you need to program a new algorithm (in the language of your choice) and find the answer to the question using your implementation. Answer the question on the site, and again, until you get the correct answer. Every week, as I said, a new algorithm. And accordingly deadlines. I was motivated by this simply crazy: I ran home from work and I did not part with the algorithms on weekends, I went on vacation, sat on top of the highest point of the country and programmed sort merge.
')
I waited six months to be announced again its beginning, to advise it to other people, because for me it was like a treasure found.
As an example, here is a picture of how I found the solvability of 2SAT problems with a random algorithm.
2SAT-problem: there is some set of Boolean variables {X1, ..., Xn}, restrictive conditions are given in the form (X1 OR X5), (¬X2 OR X3), (X5 OR X9), ... The task is to determine whether it is possible to satisfy all these conditions at the same time.
The proposed algorithm takes and randomly changes the value of one of the variables in one of the unsatisfied conditions.

In the picture on the x axis - the number of random coup d'etats (per set run), in y - the number of unsatisfied conditions. 6 different sets of such conditions were given, and it was necessary to determine which of them are solvable (satisfied) and which are not. If the set of conditions is satisfactory, then such a random alteration is a solution. If not, then the number of unsatisfied conditions begins to fluctuate around a certain value. For example, on the second left of the line in the picture, one can see that after some time the system converged to a pair of mutually unsatisfied conditions and these random alterations oscillate the system within several random variations.
Now it seems to me that these were the top 4 months of my life concentrating on interesting things when I was taking this course. And I still think, maybe you will give me advice, in which plan companies and in what positions you need to deal with such things every day.
Source: https://habr.com/ru/post/214367/
All Articles