Experience in developing an intelligent tutorial interface
In the future, traditional education in the exact sciences can be supplemented not only by MOOC (Massive Open Online Courses) courses, but also by courses in the “follow-up” intellectual tutorials. Such programs can, to some extent, evaluate a student’s decision for completeness and correctness, as well as provide hints for a solution. The figure below shows the input interface for solving the problem in the “tracking” tutorial program developed by our team:

Some idea of the algorithms underlying such programs can be found here .
In the developed program there are two input interfaces for solving the problem: “difficult” and “easy”. Below is described in more detail about each of them.
')
As steps to solve the student enters into the program formulas in LaTeX-like syntax. Formula input syntax was somewhat simplified. For example, the input matrix is as follows:
During formula input, its visual representation is dynamically formed in the form of step input. After the student enters the formula, he presses the “Check Step” button. If the step is correct, then the formula being tested is moved to the area with the title “Solution”. Otherwise, some elements of the step entry form are colored red.
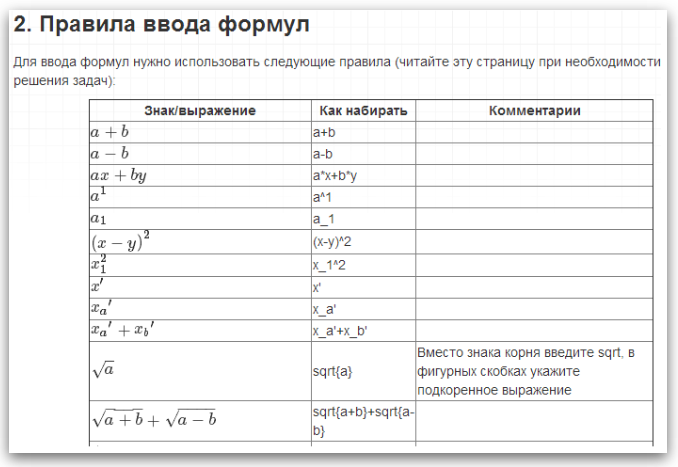
At any time, the student can look at the rules for entering formulas by clicking on the button with the appropriate name. The rules for entering formulas were written as briefly as possible, in the form of examples with explanations:
The reader may wonder why we have not built in the program a visual formula editor. The fact is that in this case, the students would send to check too many formulas, the correctness of which would be quite difficult to establish. Unfortunately, in order to make it possible to programmatically evaluate the course of a student's reasoning, it is necessary to impose restrictions on the method of inputting solution steps. The severity of restrictions as the code base of the program develops can be reduced.
In the current version of the program such restrictions apply (these are fragments from the program interface help):


The following figure shows that the student’s step is recognized as incorrect, due to the fact that the student used the notation not intended in the task settings:

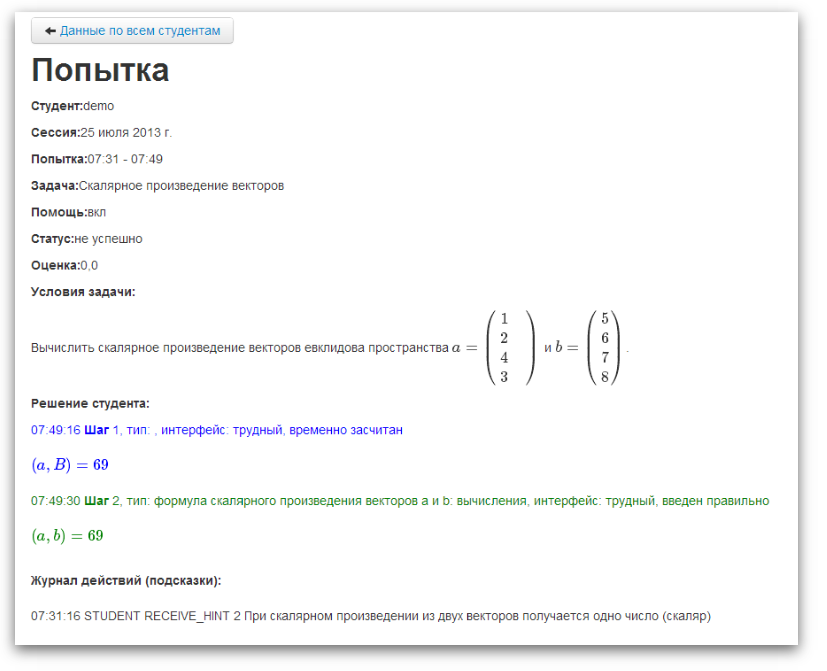
Since a student can always enter a decision step that was not intended by the author of the course, a complaint mechanism was implemented in the program, the essence of which is as follows. If, in the opinion of the student, the program is wrong, without counting his step as correct, he can click on the “Report” button. After this step will be counted as correct. Subsequently, the status of the step can be changed by the teacher. The task solutions reports are available to the teacher in the administrative panel of the application, where such steps are highlighted in color and endowed with a special status:
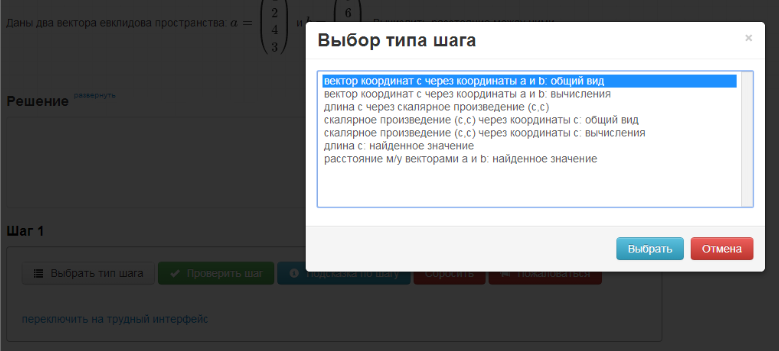
When using this interface, the student first selects the desired type of step (the types of steps are entered into the program by the author of the course):
After that, the formula formula is loaded into the step entry form:

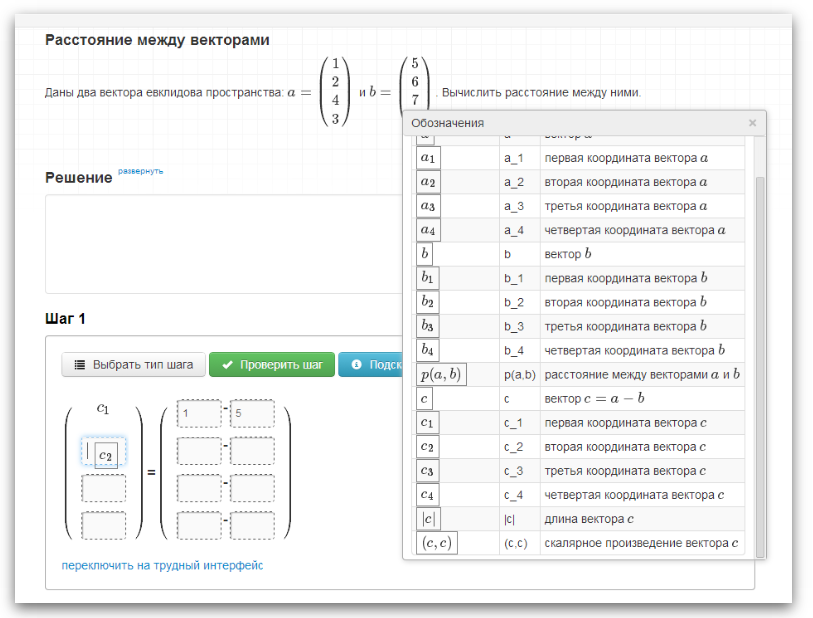
Next, the student fills in the blanks in the template, entering the numbers with his hands, and dragging the symbols from the “Legend” window:
It can be said that usability testing (or rather, its similarity, as far as strength and time allowed) was carried out twice. For the first time, several full-time students and evening students of the psychological department of one state university were caught. Students were asked to go through tutorials that help to master the program interface. The tutorials included theoretical material and two tasks. Were collected feedback from students, in addition, were analyzed videos of students in the program. The video recorded not only what was happening on the screen of the student, but his face.
For the second time, an entire group of full-time students worked in the tutorial program, which was offered the opportunity to receive an automatic evaluation for the exam in case of successful solution of problems in the tutorial program. At this stage, the videos of students' work, as well as their decisions, were analyzed.
10 students were interviewed. Below are the feedback received. From the reviews, we, firstly, excluded the uninformative type “I liked everything, no comments”, and second, we excluded what was subsequently corrected in the program. Performance data obtained from survey participants.
1. gender: wives, performance: cf.
2. gender: women, performance: higher
3. gender: women, performance: higher
4. Gender: husband, performance: Wed
5. gender: women, performance: higher
6. Gender: husband, performance: Wed
7. gender: women, performance: higher
Note that at the time of collecting feedback, in the step type selection window, not only the step types from the teacher’s recommended solution of the problem were shown, but also 2-3 randomly selected types from the database. It was assumed that in this way it would be possible to “misty” a little the problem solving plan for the student, so that he himself would think about each type of step, whether it really is needed or not. Testing has shown that having such a choice confuses even the most advanced students. Many students read the name of each type of step for a long time, trying to understand what it represents, and were not completely sure of their choice. Therefore, in the next version of the program, there are no “extra” types.
In testing participated 23 students. Both students with high academic performance and students with medium or low academic performance participated (grades are calculated on the basis of homework grades). Since the data for usability testing was collected indirectly (it was not the primary goal of the students' work in the program), no conclusions can be made on the basis of the collected data. But you can put forward a hypothesis :)
Students were asked to study the program interface, and then try to solve one or two tasks of varying complexity. Many students, in order to get a higher grade, tried to solve all three problems. Those who could not completely solve the problem in the training program, handed over to the teachers the leaflets ps solutions.
The average learning time for the program interface took 23 minutes for students with a high performance, and 32 minutes for students with an average or low progress. Two students with high performance scrolled through the program interface, but they didn’t do the exercises (one student didn’t solve any of the tasks afterwards). Not all students went through the interface tutorials as we would like. Many students, before solving problems that help to master the interface, flipped through all the pages of tutorials, trying to understand what awaits them further. Jumped through the pages of tutorials that forward and back. There were enthusiasts who solved the problem to the end and struggled to get 100% estimates, despite the fact that on the tutorial page they were asked to enter one or two steps and proceed to the next section.
Here are the wording of the tasks to help master the interface:


Some students missed learning through the “easy” or “difficult” interface and passed the material only on the interface in which they were going to solve. Other students missed out on some particular points and completely understood the subtleties of entering data into the program in the process of solving problems. One student rather interestingly studied the syntax for entering formulas. This student added one or another sign to a complex formula and watched how its visual presentation changed, as if debugging step input.
Below are data on the results of solving problems of medium and high complexity. The value of the indicator "% of incorrect steps" is calculated as the ratio of the number of steps of the student’s decision that the tutorial has marked as incorrect to the total number of steps of the student’s decision. If a student knows how to solve a problem, then the corresponding indicator value characterizes the difficulty of entering a solution for a given program interface and current restrictions on the form of the formulas entered by him. In the tables, students with high, medium and low performance are coded using the notation F, A, I.
Table 1. Data on solutions of the “Distance between vectors” task
Table 2. Data on solutions of the “Scalar products in different bases” problem
The complaint mechanism was used only by those students who solved the most difficult task. 4 students “complained” about the program, and the complaints were not justified in all cases. Incorrectly perceived steps by the program met in the decisions of 8 students, in total there were 18 such steps. An analysis of these steps showed:
Despite the presence of the “Typical errors” page, students often instead of several formulas introduced a single formula of the form
It also turned out that the program formed lower marks for the decision than this or that student had expected. The reason for this is that when entering solutions into the database of the tutorial, it was assumed that each step of the solution corresponds to two formulas: an algebraic expression with symbols and a formula with direct calculations. For example:
Students were not given instructions about the form of decision writing expected from them, and therefore they often omitted formulas corresponding to algebraic expressions. Meanwhile, the algorithm for measuring progress in solving requires first of all algebraic expressions: the more computationally folded the student's formula is, the greater the uncertainty about how he solved the problem (roughly speaking, what can be said about the student if he simply introduces a = 6?)
Quite often, students first solved the problem on paper, and then entered its solution into the training program.
Once upon a time that humanists could enter formulas in the LaTeX-like syntax, not only the teachers who provided the students for the experiments did not believe, but also the author of this post. We were all very surprised when it turned out to be wrong (thanks to Mikhail Filonenko for the insistent offer to try this very method of entering a solution).
There is room for improvement of the current version of the tutorial program developed by us. In order for the tutorial program to check not 3 puzzles on linear algebra, but much more, it is necessary to add a lot more program code.
First, it is necessary to expand the modules for translating formulas introduced using the “simplified” syntax
All these syntaxes are similar, but have their own nuances.
Secondly, one of the key places of such systems is the decision verification module. In this direction, an algorithm is being developed for measuring progress in solving a student (the description of this algorithm and its alternatives requires a separate post).

Some idea of the algorithms underlying such programs can be found here .
In the developed program there are two input interfaces for solving the problem: “difficult” and “easy”. Below is described in more detail about each of them.
')
Difficult interface
As steps to solve the student enters into the program formulas in LaTeX-like syntax. Formula input syntax was somewhat simplified. For example, the input matrix is as follows:
[1,2;3,4;5,6] During formula input, its visual representation is dynamically formed in the form of step input. After the student enters the formula, he presses the “Check Step” button. If the step is correct, then the formula being tested is moved to the area with the title “Solution”. Otherwise, some elements of the step entry form are colored red.
At any time, the student can look at the rules for entering formulas by clicking on the button with the appropriate name. The rules for entering formulas were written as briefly as possible, in the form of examples with explanations:

The reader may wonder why we have not built in the program a visual formula editor. The fact is that in this case, the students would send to check too many formulas, the correctness of which would be quite difficult to establish. Unfortunately, in order to make it possible to programmatically evaluate the course of a student's reasoning, it is necessary to impose restrictions on the method of inputting solution steps. The severity of restrictions as the code base of the program develops can be reduced.
In the current version of the program such restrictions apply (these are fragments from the program interface help):


The following figure shows that the student’s step is recognized as incorrect, due to the fact that the student used the notation not intended in the task settings:

Since a student can always enter a decision step that was not intended by the author of the course, a complaint mechanism was implemented in the program, the essence of which is as follows. If, in the opinion of the student, the program is wrong, without counting his step as correct, he can click on the “Report” button. After this step will be counted as correct. Subsequently, the status of the step can be changed by the teacher. The task solutions reports are available to the teacher in the administrative panel of the application, where such steps are highlighted in color and endowed with a special status:

"Easy" interface
When using this interface, the student first selects the desired type of step (the types of steps are entered into the program by the author of the course):

After that, the formula formula is loaded into the step entry form:

Next, the student fills in the blanks in the template, entering the numbers with his hands, and dragging the symbols from the “Legend” window:

Testing both interfaces
It can be said that usability testing (or rather, its similarity, as far as strength and time allowed) was carried out twice. For the first time, several full-time students and evening students of the psychological department of one state university were caught. Students were asked to go through tutorials that help to master the program interface. The tutorials included theoretical material and two tasks. Were collected feedback from students, in addition, were analyzed videos of students in the program. The video recorded not only what was happening on the screen of the student, but his face.
For the second time, an entire group of full-time students worked in the tutorial program, which was offered the opportunity to receive an automatic evaluation for the exam in case of successful solution of problems in the tutorial program. At this stage, the videos of students' work, as well as their decisions, were analyzed.
Student reviews after the first "usability testing"
10 students were interviewed. Below are the feedback received. From the reviews, we, firstly, excluded the uninformative type “I liked everything, no comments”, and second, we excluded what was subsequently corrected in the program. Performance data obtained from survey participants.
1. gender: wives, performance: cf.
What we liked: there is an opportunity to solve a task for a person with a lack of knowledge. Tips help a lot. What did not like: too long to decide, a lot to press the buttons. Manually, for example, you can solve the quadratic equation faster than with this program.
2. gender: women, performance: higher
The program is convenient because it has everything you need on the network. No need to install and wait. It works fast. With quadratic equations, we had to work only in entering the accepted notation. Easy, affordable, comfortable
3. gender: women, performance: higher
It was pleasant: that there are all necessary functions, there are hints. Works without fail. Did not like it: too long to enter the steps.
4. Gender: husband, performance: Wed
It is very convenient that the menu “add step, get hint” and hints move along with the cursor on the screen so that they are always visible. The inconvenience was caused by the fact that when an error occurred, the computer highlights the whole expression in red, and not the place that cannot be counted, you have to look for an error.
5. gender: women, performance: higher
Conveniently, only there is the likelihood of doing extra work, in the case when the coefficients = 1, and they must be divided or multiplied. I liked: there are tips.
6. Gender: husband, performance: Wed
I liked the usual input of mathematical signs and signs of functions. <...>
7. gender: women, performance: higher
I liked that you can quickly and conveniently enter characters with the help of the training manual. Convenient interface, everything is quite clear. When you get used to the layout of the macbook, you can manipulate it quickly. <...> When the answer is wrong - there are no comments to the error - it would be more convenient if there was such a function. It’s more usual to count on a sheet, so I think if I were offered to use the program now, I would first decide on the sheet and then enter the results in the windows. If there was such a program at school, it might be easier to study.
Note that at the time of collecting feedback, in the step type selection window, not only the step types from the teacher’s recommended solution of the problem were shown, but also 2-3 randomly selected types from the database. It was assumed that in this way it would be possible to “misty” a little the problem solving plan for the student, so that he himself would think about each type of step, whether it really is needed or not. Testing has shown that having such a choice confuses even the most advanced students. Many students read the name of each type of step for a long time, trying to understand what it represents, and were not completely sure of their choice. Therefore, in the next version of the program, there are no “extra” types.
The results of the second "usability testing"
In testing participated 23 students. Both students with high academic performance and students with medium or low academic performance participated (grades are calculated on the basis of homework grades). Since the data for usability testing was collected indirectly (it was not the primary goal of the students' work in the program), no conclusions can be made on the basis of the collected data. But you can put forward a hypothesis :)
Students were asked to study the program interface, and then try to solve one or two tasks of varying complexity. Many students, in order to get a higher grade, tried to solve all three problems. Those who could not completely solve the problem in the training program, handed over to the teachers the leaflets ps solutions.
The average learning time for the program interface took 23 minutes for students with a high performance, and 32 minutes for students with an average or low progress. Two students with high performance scrolled through the program interface, but they didn’t do the exercises (one student didn’t solve any of the tasks afterwards). Not all students went through the interface tutorials as we would like. Many students, before solving problems that help to master the interface, flipped through all the pages of tutorials, trying to understand what awaits them further. Jumped through the pages of tutorials that forward and back. There were enthusiasts who solved the problem to the end and struggled to get 100% estimates, despite the fact that on the tutorial page they were asked to enter one or two steps and proceed to the next section.
Here are the wording of the tasks to help master the interface:


Some students missed learning through the “easy” or “difficult” interface and passed the material only on the interface in which they were going to solve. Other students missed out on some particular points and completely understood the subtleties of entering data into the program in the process of solving problems. One student rather interestingly studied the syntax for entering formulas. This student added one or another sign to a complex formula and watched how its visual presentation changed, as if debugging step input.
Below are data on the results of solving problems of medium and high complexity. The value of the indicator "% of incorrect steps" is calculated as the ratio of the number of steps of the student’s decision that the tutorial has marked as incorrect to the total number of steps of the student’s decision. If a student knows how to solve a problem, then the corresponding indicator value characterizes the difficulty of entering a solution for a given program interface and current restrictions on the form of the formulas entered by him. In the tables, students with high, medium and low performance are coded using the notation F, A, I.
Table 1. Data on solutions of the “Distance between vectors” task
| No | Performance | Solved,% | Cost t min | % wrong steps | Total number of steps |
| one | I | one | 29 | 0.52 | 27 |
| 2 | I | one | nineteen | 0.44 | sixteen |
| 3 | A | one | 12 | 0.09 | eleven |
| four | A | one | 24 | 0.76 | 29 |
| five | A | one | 29 | 0.56 | 23 |
| 6 | A | one | 33 | 0.42 | 12 |
| 7 | A | one | 21 | 0.6 | thirty |
| eight | F | one | 13 | 0.22 | 9 |
| 9 | F | one | ten | 0.1 | ten |
| ten | F | one | 7 | 0 | ten |
| eleven | F | 0 | one | one | 2 |
Table 2. Data on solutions of the “Scalar products in different bases” problem
| No | Performance | Solved,% | Cost t min | % wrong steps | Total number of steps |
| one | I | 0.9 | 33 | 0.46 | 28 |
| 2 | A | one | 35 | 0.62 | 29 |
| 3 | A | 0.8 | 33 | 0.12 | 17 |
| four | A | 0.5 | 23 | 0.45 | 22 |
| five | A | 0.5 | 80 | 0.41 | 54 |
| 6 | A | 0.9 | 26 | 0.17 | thirty |
| 7 | F | 0.5 | 80 | 0.76 | 49 |
| eight | F | 0.5 | 43 | 0.73 | 25 |
| 9 | F | 0.5 | 18 | 0.25 | sixteen |
| ten | F | 0.5 | 39 | 0.2 | 15 |
| eleven | F | 0.2 | 70 | 0.79 | 29 |
| 12 | F | one | 78 | 0.61 | 18 |
| 13 | F | 0.7 | 63 | 0.8 | 25 |
| 14 | F | one | 32 | 0.32 | 34 |
| 15 | F | one | 22 | 0.17 | 23 |
The complaint mechanism was used only by those students who solved the most difficult task. 4 students “complained” about the program, and the complaints were not justified in all cases. Incorrectly perceived steps by the program met in the decisions of 8 students, in total there were 18 such steps. An analysis of these steps showed:
- the most common cause was unintended formulas (i.e. not all possible solutions to the problem were included in the program);
- A common cause of incorrect recognition by the system of entered formulas was the case when, instead of entering formulas in an easy-to-use interface, with the help of pereaskivaniya symbols, the student entered the characters independently from the keyboard. This can be considered a very useful comment on the intuitive lightweight interface. It was necessary to provide such an input script.
Despite the presence of the “Typical errors” page, students often instead of several formulas introduced a single formula of the form
(c,c) = (1-3)^2 + (2-4)^2 = 8 or (c,c) = (1-3)^2 + (2-4)^2, (c,c) = 8 and only after that they clicked on the “Check step” button.It also turned out that the program formed lower marks for the decision than this or that student had expected. The reason for this is that when entering solutions into the database of the tutorial, it was assumed that each step of the solution corresponds to two formulas: an algebraic expression with symbols and a formula with direct calculations. For example:
(a,b) = x_a*x_b+y_a*y_b and (a,b) = 1*2+3*4 Students were not given instructions about the form of decision writing expected from them, and therefore they often omitted formulas corresponding to algebraic expressions. Meanwhile, the algorithm for measuring progress in solving requires first of all algebraic expressions: the more computationally folded the student's formula is, the greater the uncertainty about how he solved the problem (roughly speaking, what can be said about the student if he simply introduces a = 6?)
Quite often, students first solved the problem on paper, and then entered its solution into the training program.
Conclusion
Once upon a time that humanists could enter formulas in the LaTeX-like syntax, not only the teachers who provided the students for the experiments did not believe, but also the author of this post. We were all very surprised when it turned out to be wrong (thanks to Mikhail Filonenko for the insistent offer to try this very method of entering a solution).
There is room for improvement of the current version of the tutorial program developed by us. In order for the tutorial program to check not 3 puzzles on linear algebra, but much more, it is necessary to add a lot more program code.
First, it is necessary to expand the modules for translating formulas introduced using the “simplified” syntax
- in the syntax Mathjax (a library that helps to dynamically form a visual representation of the formula entered by the student);
- in syntax that the SymPy library of symbolic computations will understand, which is used to verify students' decisions.
All these syntaxes are similar, but have their own nuances.
Secondly, one of the key places of such systems is the decision verification module. In this direction, an algorithm is being developed for measuring progress in solving a student (the description of this algorithm and its alternatives requires a separate post).
Brief on software implementation
- Server language and framework - Python + Django,
- Formula validation logic - its own heuristic algorithms + SymPy (Python),
- Client - JavaScript + jQuery + MathJax,
- Client decoration - Twitter Bootstrap.
Thanks
- Legato_di Dmitry Dushkin for relentless advising on various technical issues and assistance in the preparation of this post,
- A.Yu. Schwartz and A.N. Krichevets for helping to create content for the tutorial and the students provided,
- Anatoly Panin for the development of the alpha version of the program.
Source: https://habr.com/ru/post/213181/
All Articles