AES-128. Details and implementation in python
The idea of writing something encryptive for yourself was born rather trivial - I had to start another debit card and, therefore, keep another PIN code in my head. Paranoia does not allow storing such information in the clear, and also uses third-party services, so after some searches I stopped at the AES standard. I immediately wanted to understand and implement the algorithm myself, without resorting to additional modules.
In the article I will tell in detail about the components of the algorithm, a little dip in the mat part and give an example implementation in python. In development, I was limited only to what is included in the standard library.
Advanced Encryption Standard is the well-known name of the Rijndael algorithm ([rɛindaːl]), which was developed by two Belgian cryptographers Joan Dimen and Vincent Raim. The algorithm is block and symmetric. Adopted as a data encryption standard for government agencies in the United States. The recently acclaimed National Security Agency uses it to store documents: down to the SECRET level, encryption with a key length of 128 bits is used, the TOP SECRET information requires a key of 192 or 256 bits. In addition to high cryptographic strength, the algorithm is based on not the most difficult mathematics.
To work, we need a set of bytes as an encryption object and a secret key that will be required when decrypting. It is inconvenient to keep long keys in the head, and it is believed that the key length is 128 bits, more than enough for inaccessibility, so I did not look at options 192/256. In addition, as stated here , under certain conditions a longer key may lag behind in stability.
')
We introduce some notation:
The algorithm has four transformations, each of which affects the state in its own way and ultimately leads to the result: SubBytes (), ShiftRows (), MixColumns () and AddRoundKey () . The general encryption scheme can be represented as:
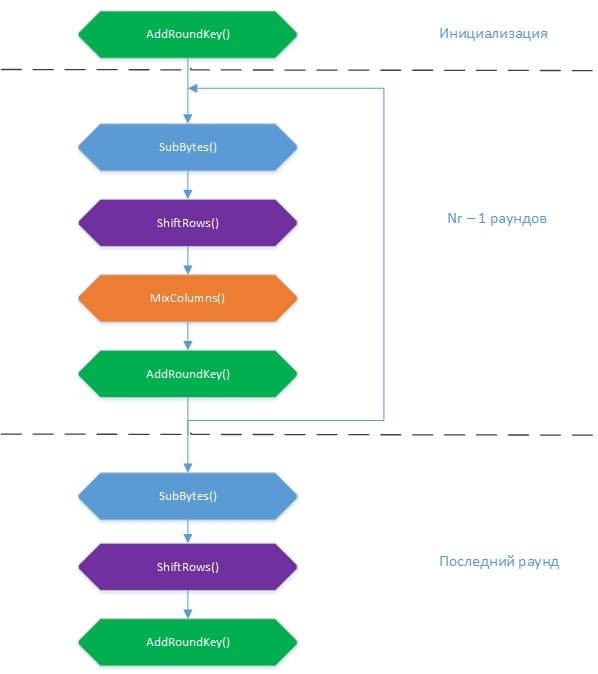
At the beginning, the State array is filled with input values according to the formula State [r] [c] = input [r + 4c], r = 0.1 ... 4; c = 0.1..Nb . That is, the columns. A block of 16 bytes is encrypted at a time.

The algorithm operates on bytes, considering them to be elements of a finite field or a Galois field GF (2 8 ). The number in brackets is the number of field elements or its power. The elements of the field GF (2 8 ) are polynomials of degree at most 7, which can be given by a line of their coefficients. Bytes are very easy to imagine as a polynomial. For example, byte {1,1,1,0,0,0,1,1} corresponds to the field element 1x 7 + 1x 6 + 1x 5 + 0x 4 + 0x 3 + 0x 2 + 1x 1 + 1x 0 = 1x 7 + 1x 6 + 1x 5 + x +1. The fact that we work with field elements is very important because it changes the rules of the operations of addition and multiplication. This we touch on later.
Next, we consider in detail each of the transformations.
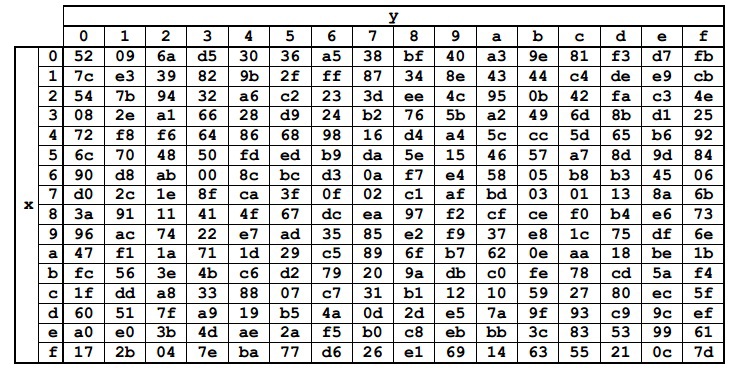
A conversion is the replacement of each byte from State with its corresponding Sbox constant table. The values of the Sbox elements are represented in hexadecimal notation. The table itself is obtained by means of transformations of the field GF (2 8 ) already known to us.
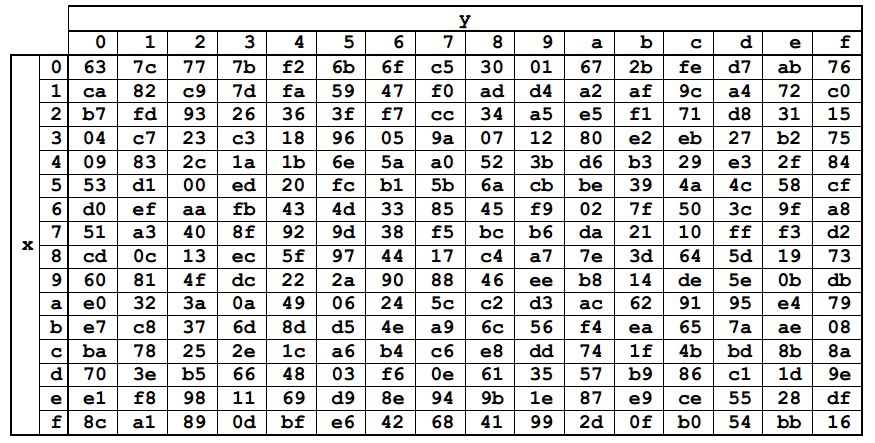
Each byte from State can be represented as {xy} in hexadecimal notation. Then it should be replaced with an element at the intersection of row x and column y. For example, {6e} will be replaced by {9f}, and {15} by {59}.
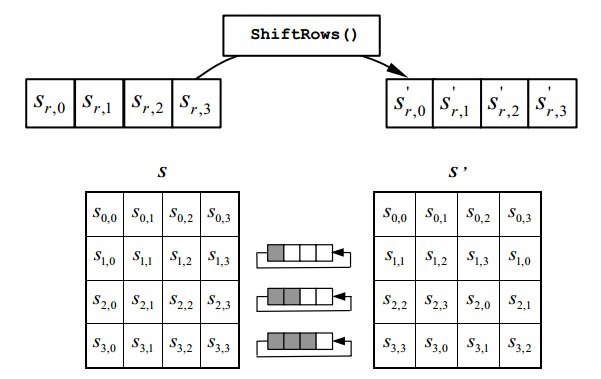
Simple transformation. It performs a cyclic left shift by 1 element for the first row, by 2 for the second and by 3 for the third. The zero line does not move.
Within the framework of this transformation, each column in State is represented as a polynomial and multiplied in the GF (2 8 ) field modulo x 4 + 1 with a fixed polynomial 3x 3 + x 2 + x + 2. It sounds like a simple, but hardly understandable way . The picture becomes easier if you look at the equivalent matrix entry provided in the official document of the standard:

When multiplying matrices, the value of a ij is obtained as the sum of the products of the corresponding elements of the i-th row of the first matrix and the j-th column of the second, i.e.
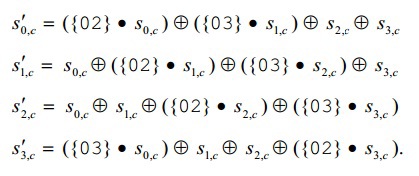
Here we need to recall the inoperability of the usual rules of addition and multiplication.
New rules:
Naturally, these are not general rules of arithmetic in a finite field, but within the framework of the algorithm, it is necessary to multiply by three constants for encryption and four for decryption, so there will be enough of such local life hacks.
MixColumns () together with ShiftRows () adds diffusion to the cipher.
The transformation produces a bitwise XOR of each element in the State with the corresponding element in the RoundKey. RoundKey is an array of the same size as State, which is built for each round based on the secret key by the KeyExpansion () function, which we will consider further.
This auxiliary transformation forms a set of round keys - KeySchedule. KeySchedule is a long table consisting of Nb * (Nr + 1) columns or (Nr + 1) blocks, each of which is equal in size to State. The first round key is filled based on the secret key that you come up with, according to the formula
KeySchedule [r] [c] = SecretKey [r + 4c], r = 0.1 ... 4; c = 0.1..Nk.
It is clear that in KeySchedule we have to enter bytes so that further operations are possible. If you use this algorithm for home encryption, then storing a sequence of numbers in your head is not at all comfortable, so in our implementation KeyExpansion () will take the plaintext line as an input and use

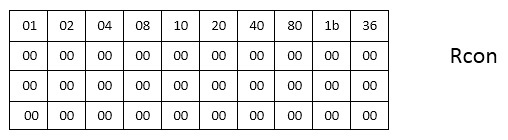
The figure shows the KeySchedule layout for AES-128: 11 blocks with 4 columns. For other variations of the algorithm, there will be (Nr + 1) blocks of Nb columns, respectively. Now we have to fill the empty places. For conversions, a constant table is again defined - Rcon - whose values are in hexadecimal notation.
KeySchedule replenishment algorithm:
This auxiliary transformation is the most voluminous in writing and, probably, the most complex, after comprehension of mathematics in MixColumns (), in the algorithm. The cipher key must consist of 4 * Nk elements (in our case 16). But since we do all this for home use, it is quite likely that not everyone will come up with a 16-character key and remember it. Therefore, if an input line has a length of less than 16, I will enter the {01} values to the norm in KeySchedule.
As mentioned earlier, KeySchedule is used in the transformation AddRoundKey (). In the round of initialization, the round key will be columns with numbers 0, .., 3, in the first one - with numbers 4, .., 7 and so on. The whole point of AddRoundKey () is to generate an XOR State and a round key.
This is, in fact, all that concerns the encryption process. The output array of encrypted bytes is composed of State according to the formula output [r + 4c] = State [r] [c], r = 0.1 ... 4; c = 0.1..Nb . In the meantime, the article is being dragged out, so now we will quickly run through the decryption procedure.
The idea here is simple: if you perform a sequence of transformations inverse with encryption transformations with the same keyword, you will get the original message. Such inverse transformations are InvSubBytes (), InvShiftRows (), InvMixColumns () and AddRoundKey () . General scheme of the decryption algorithm:
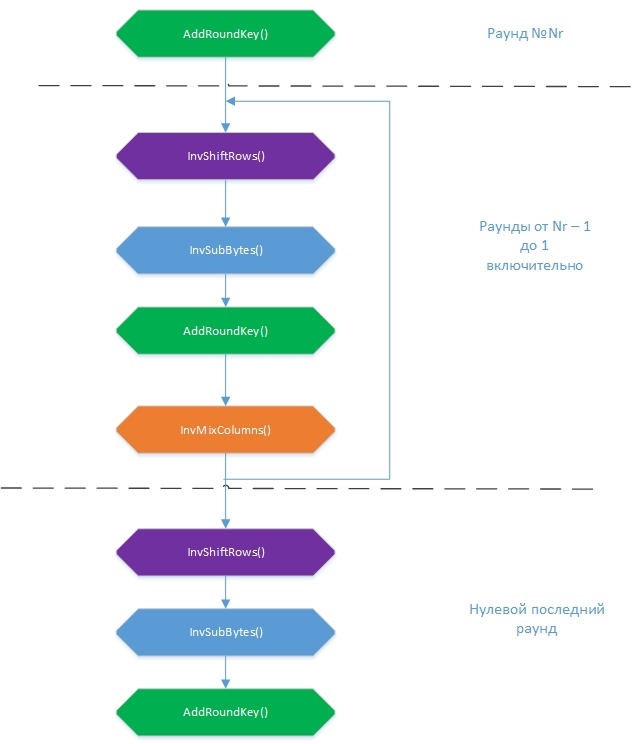
It should be noted that the sequence of adding round keys to AddRoundKey () must be reversed: from Nr + 1 to 0. Initially, as with encryption, the State table is formed from the array of input bytes. Then, transformations are performed on it in each round, at the end of which the decrypted file should turn out. The order of transformations has changed a bit. What will be the first, InvSubBytes () or InvShiftRows (), is actually not important, because one of them works with the values of bytes, and the second rearranges the bytes, without changing these same values, but I followed the sequence of transformations in the pseudocode of the standard.
It works in the same way as SubBytes (), except that replacements are made from the InvSbox constant table.
The remaining reverse transformations will also be very similar to their direct counterparts, therefore, in the code, we do not allocate separate functions for them. Each function describing the transformation will have an input variable
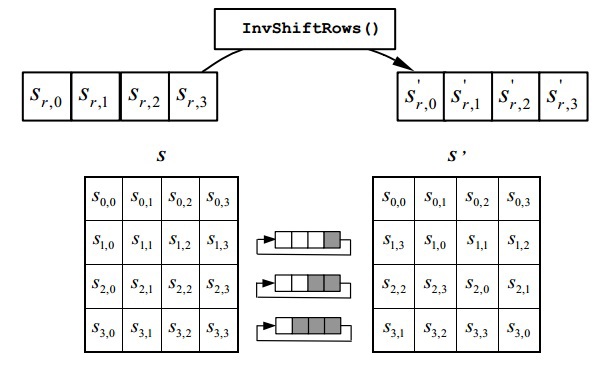
The transformation makes a cyclical shift to the right by 1 element for the first line of the State, by 2 for the second and by 3 for the third. The zero line does not rotate.
Explanation of the code:
The operations are the same, but each State column is multiplied with another polynomial {0b} x 3 + {0d} x 2 + {09} x + {0e}. In matrix form, it looks like this:

Or ready-made formulas. All values, of course, in hexadecimal notation.

Here we need to make a digression towards mathematics and explain how to get the functions of multiplication by constants larger than {02}. As I said, they are obtained by decomposing them through {01} and {02}, namely:
Of course, you can decompose the numbers in a different way, but personally verified that the decomposition
n * {09} = n * {03} + n * {03} + n * {03}
and the call of the corresponding functions will give an incorrect result (reference tables with results are in one of the links in the list of sources). Specially left alternative (commented) computational options, because they are clearer, more elegant, but for some reason they do not work correctly.
Explanation of the code: the
This transformation is inverse to itself due to the properties of the XOR operation:
Therefore, no changes need to be made. The set of round keys is formed in the same way as for encryption using the KeyExpansion () function, but round keys must be substituted in the reverse order.
Now we have a comprehensive set of auxiliary transformation functions to write
These two functions take as input a list of bytes not encrypted or encrypted, and plaintext a string with a secret keyword.
The article was quite long. I tried to dilute the text with pictures and, I hope, it was interesting for you and nobody got bored. The code presented in the article is not entirely exhaustive. I did not insert the global declaration of constant tables, small functions for MixColumns (), but explained only in words that they exist somewhere. Do not think that I am PR, but you can take the complete code glued together in the repository . There is also a modest CLI interface that allows you to simply specify the path to the file, enter the secret key and get the encrypted file in the same directory as the source (you can get the decrypted file in the same way). Encrypt for health!
And at the end it is necessary to say about one important nuance - padding or addition to the block. AES is a block encryption algorithm, the
So I did (although the first option remained, just commented out. Suddenly, it will come in handy).
Selection of sources:
In the article I will tell in detail about the components of the algorithm, a little dip in the mat part and give an example implementation in python. In development, I was limited only to what is included in the standard library.
Little introduction
Advanced Encryption Standard is the well-known name of the Rijndael algorithm ([rɛindaːl]), which was developed by two Belgian cryptographers Joan Dimen and Vincent Raim. The algorithm is block and symmetric. Adopted as a data encryption standard for government agencies in the United States. The recently acclaimed National Security Agency uses it to store documents: down to the SECRET level, encryption with a key length of 128 bits is used, the TOP SECRET information requires a key of 192 or 256 bits. In addition to high cryptographic strength, the algorithm is based on not the most difficult mathematics.
A lot of encryption
To work, we need a set of bytes as an encryption object and a secret key that will be required when decrypting. It is inconvenient to keep long keys in the head, and it is believed that the key length is 128 bits, more than enough for inaccessibility, so I did not look at options 192/256. In addition, as stated here , under certain conditions a longer key may lag behind in stability.
')
We introduce some notation:
- State is an intermediate result of encryption, which can be represented as a rectangular byte array having 4 rows and Nb columns. Each State cell contains a value of 1 byte.
- Nb is the number of columns (32-bit words) that make up the State. For the standard is regulated Nb = 4
- Nk - key length in 32-bit words. For AES, Nk = 4, 6, 8. We have already decided that we will use Nk = 4
- Nr is the number of encryption rounds. Depending on the key length, Nr = 10, 12 or 14
The algorithm has four transformations, each of which affects the state in its own way and ultimately leads to the result: SubBytes (), ShiftRows (), MixColumns () and AddRoundKey () . The general encryption scheme can be represented as:

At the beginning, the State array is filled with input values according to the formula State [r] [c] = input [r + 4c], r = 0.1 ... 4; c = 0.1..Nb . That is, the columns. A block of 16 bytes is encrypted at a time.

The algorithm operates on bytes, considering them to be elements of a finite field or a Galois field GF (2 8 ). The number in brackets is the number of field elements or its power. The elements of the field GF (2 8 ) are polynomials of degree at most 7, which can be given by a line of their coefficients. Bytes are very easy to imagine as a polynomial. For example, byte {1,1,1,0,0,0,1,1} corresponds to the field element 1x 7 + 1x 6 + 1x 5 + 0x 4 + 0x 3 + 0x 2 + 1x 1 + 1x 0 = 1x 7 + 1x 6 + 1x 5 + x +1. The fact that we work with field elements is very important because it changes the rules of the operations of addition and multiplication. This we touch on later.
Next, we consider in detail each of the transformations.
SybButes ()
A conversion is the replacement of each byte from State with its corresponding Sbox constant table. The values of the Sbox elements are represented in hexadecimal notation. The table itself is obtained by means of transformations of the field GF (2 8 ) already known to us.

Each byte from State can be represented as {xy} in hexadecimal notation. Then it should be replaced with an element at the intersection of row x and column y. For example, {6e} will be replaced by {9f}, and {15} by {59}.
ShiftRows ()
Simple transformation. It performs a cyclic left shift by 1 element for the first row, by 2 for the second and by 3 for the third. The zero line does not move.

MixColumns ()
Within the framework of this transformation, each column in State is represented as a polynomial and multiplied in the GF (2 8 ) field modulo x 4 + 1 with a fixed polynomial 3x 3 + x 2 + x + 2. It sounds like a simple, but hardly understandable way . The picture becomes easier if you look at the equivalent matrix entry provided in the official document of the standard:

When multiplying matrices, the value of a ij is obtained as the sum of the products of the corresponding elements of the i-th row of the first matrix and the j-th column of the second, i.e.
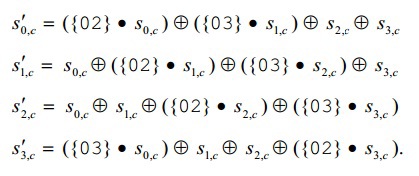
Here we need to recall the inoperability of the usual rules of addition and multiplication.
New rules:
- Adding to the GF (2 8 ) field is equivalent to the XOR operation
- Multiplication by {01} does not change multiply
- Multiplication by {02} is made according to the rule: if the multiplied value is less than {80}, it is shifted to the left by 1 bit. If the multiplied value is greater than or equal to {80}, it is first shifted to the left by 1 bit, and then an XOR operation with the value {1b} is applied to the shift result. The result can jump beyond the value of {ff}, that is, beyond the boundaries of one byte. In this case, you need to return the remainder of dividing the result by {100}.
- Multiplication by other constants can be expressed through previous
Naturally, these are not general rules of arithmetic in a finite field, but within the framework of the algorithm, it is necessary to multiply by three constants for encryption and four for decryption, so there will be enough of such local life hacks.
MixColumns () together with ShiftRows () adds diffusion to the cipher.
AddRoundKey ()
The transformation produces a bitwise XOR of each element in the State with the corresponding element in the RoundKey. RoundKey is an array of the same size as State, which is built for each round based on the secret key by the KeyExpansion () function, which we will consider further.
KeyExpansion ()
This auxiliary transformation forms a set of round keys - KeySchedule. KeySchedule is a long table consisting of Nb * (Nr + 1) columns or (Nr + 1) blocks, each of which is equal in size to State. The first round key is filled based on the secret key that you come up with, according to the formula
KeySchedule [r] [c] = SecretKey [r + 4c], r = 0.1 ... 4; c = 0.1..Nk.
It is clear that in KeySchedule we have to enter bytes so that further operations are possible. If you use this algorithm for home encryption, then storing a sequence of numbers in your head is not at all comfortable, so in our implementation KeyExpansion () will take the plaintext line as an input and use
ord() for each of the characters to write the result to the KeySchedule cells. Hence the limitations: no more than 16 characters long and, since we work with bytes, the ord() character should not return values larger than 255 or 11111111 in binary, otherwise we will get incorrect encryption at the output. It turns out that it will not be possible to encrypt using a key in Russian.
The figure shows the KeySchedule layout for AES-128: 11 blocks with 4 columns. For other variations of the algorithm, there will be (Nr + 1) blocks of Nb columns, respectively. Now we have to fill the empty places. For conversions, a constant table is again defined - Rcon - whose values are in hexadecimal notation.

KeySchedule replenishment algorithm:
- At each iteration we work with a table column. Columns 0, .., (Nk - 1) are already pre-filled with the values from the secret word. We start with the column number Nk (in our case, the fourth)
- If the W i column number is a multiple of Nk (in our case, every fourth), then we take the W i-1 column, perform a cyclic left shift on it by one element, then replace all the bytes of the column with the corresponding ones from the Sbox table, as we did in SubBytes () . Next, perform the XOR operation between the W i-Nk column, the modified W i-1 and the Rcon i / Nk-1 column. The result is written to the column W i . To make it a little clearer, the illustration for i = 4.
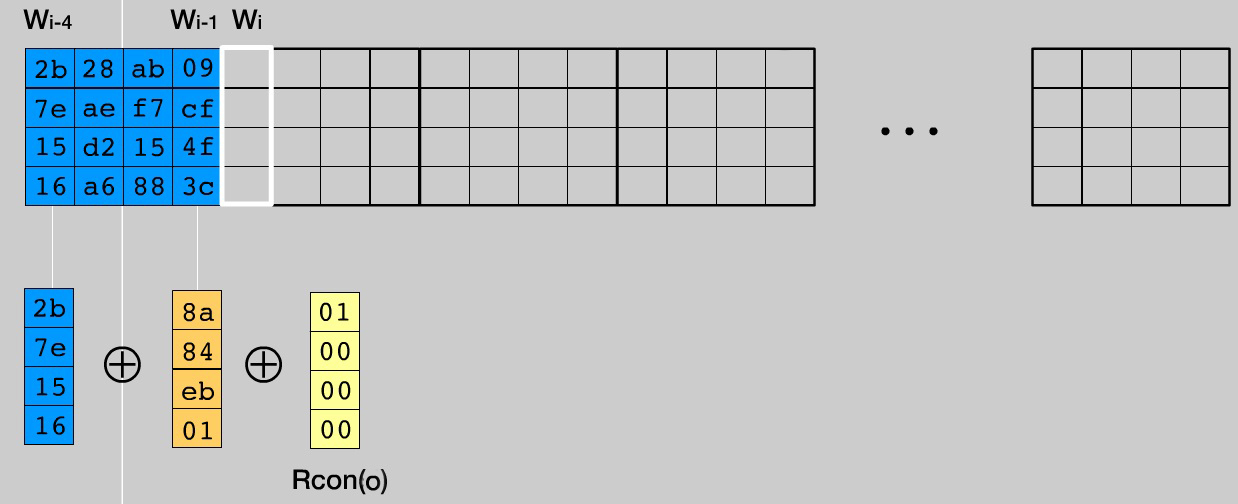
- For the remaining columns, perform XOR between W i-Nk and W i-1 . The result is recorded in W i
This auxiliary transformation is the most voluminous in writing and, probably, the most complex, after comprehension of mathematics in MixColumns (), in the algorithm. The cipher key must consist of 4 * Nk elements (in our case 16). But since we do all this for home use, it is quite likely that not everyone will come up with a 16-character key and remember it. Therefore, if an input line has a length of less than 16, I will enter the {01} values to the norm in KeySchedule.
KeyExpansion Code ()
def key_expansion(key): key_symbols = [ord(symbol) for symbol in key] # ChipherKey shoul contain 16 symbols to fill 4*Nk table. If it's less # complement the key with "0x01" if len(key_symbols) < 4*nk: for i in range(4*nk - len(key_symbols)): key_symbols.append(0x01) # make ChipherKey(which is base of KeySchedule) key_schedule = [[] for i in range(4)] for r in range(4): for c in range(nk): key_schedule[r].append(key_symbols[r + 4*c]) # Comtinue to fill KeySchedule for col in range(nk, nb*(nr + 1)): # col - column number if col % nk == 0: # take shifted (col - 1)th column... tmp = [key_schedule[row][col-1] for row in range(1, 4)] tmp.append(key_schedule[0][col-1]) # change its elements using Sbox-table like in SubBytes... for j in range(len(tmp)): sbox_row = tmp[j] // 0x10 sbox_col = tmp[j] % 0x10 sbox_elem = sbox[16*sbox_row + sbox_col] tmp[j] = sbox_elem # and finally make XOR of 3 columns for row in range(4): s = key_schedule[row][col - 4]^tmp[row]^rcon[row][col/nk - 1] key_schedule[row].append(s) else: # just make XOR of 2 columns for row in range(4): s = key_schedule[row][col - 4]^key_schedule[row][col - 1] key_schedule[row].append(s) return key_schedule As mentioned earlier, KeySchedule is used in the transformation AddRoundKey (). In the round of initialization, the round key will be columns with numbers 0, .., 3, in the first one - with numbers 4, .., 7 and so on. The whole point of AddRoundKey () is to generate an XOR State and a round key.
This is, in fact, all that concerns the encryption process. The output array of encrypted bytes is composed of State according to the formula output [r + 4c] = State [r] [c], r = 0.1 ... 4; c = 0.1..Nb . In the meantime, the article is being dragged out, so now we will quickly run through the decryption procedure.
Quick decoding
The idea here is simple: if you perform a sequence of transformations inverse with encryption transformations with the same keyword, you will get the original message. Such inverse transformations are InvSubBytes (), InvShiftRows (), InvMixColumns () and AddRoundKey () . General scheme of the decryption algorithm:

It should be noted that the sequence of adding round keys to AddRoundKey () must be reversed: from Nr + 1 to 0. Initially, as with encryption, the State table is formed from the array of input bytes. Then, transformations are performed on it in each round, at the end of which the decrypted file should turn out. The order of transformations has changed a bit. What will be the first, InvSubBytes () or InvShiftRows (), is actually not important, because one of them works with the values of bytes, and the second rearranges the bytes, without changing these same values, but I followed the sequence of transformations in the pseudocode of the standard.
InvSubBytes ()
It works in the same way as SubBytes (), except that replacements are made from the InvSbox constant table.

The remaining reverse transformations will also be very similar to their direct counterparts, therefore, in the code, we do not allocate separate functions for them. Each function describing the transformation will have an input variable
inv . If it is False , then the function will work in normal or direct mode (encryption), if True - in inverse (decryption).Code
def sub_bytes(state, inv=False): if inv == False: # encrypt box = sbox else: # decrypt box = inv_sbox for i in range(len(state)): for j in range(len(state[i])): row = state[i][j] // 0x10 col = state[i][j] % 0x10 # Our Sbox is a flat array, not a bable. So, we use this trich to find elem: box_elem = box[16*row + col] state[i][j] = box_elem return state InvShiftRows ()
The transformation makes a cyclical shift to the right by 1 element for the first line of the State, by 2 for the second and by 3 for the third. The zero line does not rotate.

Explanation of the code:
left_shift/right_shift(array, count) rotate the input array in the appropriate direction count timesCode
def shift_rows(state, inv=False): count = 1 if inv == False: # encrypting for i in range(1, nb): state[i] = left_shift(state[i], count) count += 1 else: # decryption for i in range(1, nb): state[i] = right_shift(state[i], count) count += 1 return state InvMixColumns ()
The operations are the same, but each State column is multiplied with another polynomial {0b} x 3 + {0d} x 2 + {09} x + {0e}. In matrix form, it looks like this:

Or ready-made formulas. All values, of course, in hexadecimal notation.

Here we need to make a digression towards mathematics and explain how to get the functions of multiplication by constants larger than {02}. As I said, they are obtained by decomposing them through {01} and {02}, namely:
Transformations
n * {03} = n * ({02} + {01}) = n * {02} + n * {01}
n * {09} = n * ({08} + {01}) = n * {02} * {02} * {02} + n * {01}
n * {0b} = n * ({08} + {02} + {01}) = b * {02} * {02} * {02} + n * {02} + n * {01}
n * {0d} = n * ({08} + {04} + {01}) = n * {08} + n * {04} + n * {01} = n * {02} * {02} * {02} + n * {02} * {02} + n * {01}
n * {0} = n * ({08} + {04} + {02} = n * {08} + n * {04} + n * {02} = n * {02} * {02} * { 02} + n * {02} * {02} + b * {02}
n * {09} = n * ({08} + {01}) = n * {02} * {02} * {02} + n * {01}
n * {0b} = n * ({08} + {02} + {01}) = b * {02} * {02} * {02} + n * {02} + n * {01}
n * {0d} = n * ({08} + {04} + {01}) = n * {08} + n * {04} + n * {01} = n * {02} * {02} * {02} + n * {02} * {02} + n * {01}
n * {0} = n * ({08} + {04} + {02} = n * {08} + n * {04} + n * {02} = n * {02} * {02} * { 02} + n * {02} * {02} + b * {02}
Of course, you can decompose the numbers in a different way, but personally verified that the decomposition
n * {09} = n * {03} + n * {03} + n * {03}
and the call of the corresponding functions will give an incorrect result (reference tables with results are in one of the links in the list of sources). Specially left alternative (commented) computational options, because they are clearer, more elegant, but for some reason they do not work correctly.
Auxiliary functions of multiplication
def mul_by_02(num): if num < 0x80: res = (num << 1) else: res = (num << 1)^0x1b return res % 0x100 def mul_by_03(num): return mul_by_02(num)^num def mul_by_09(num): #return mul_by_03(num)^mul_by_03(num)^mul_by_03(num) - works wrong, I don't know why return mul_by_02(mul_by_02(mul_by_02(num)))^num def mul_by_0b(num): #return mul_by_09(num)^mul_by_02(num) return mul_by_02(mul_by_02(mul_by_02(num)))^mul_by_02(num)^num def mul_by_0d(num): #return mul_by_0b(num)^mul_by_02(num) return mul_by_02(mul_by_02(mul_by_02(num)))^mul_by_02(mul_by_02(num))^num def mul_by_0e(num): #return mul_by_0d(num)^num return mul_by_02(mul_by_02(mul_by_02(num)))^mul_by_02(mul_by_02(num))^mul_by_02(num) Explanation of the code: the
mul_by_<> functions perform multiplication by the corresponding constant in GF (2 8 ) according to the rules described in the section about MixColumns () .Code
def mix_columns(state, inv=False): for i in range(nb): if inv == False: # encryption s0 = mul_by_02(state[0][i])^mul_by_03(state[1][i])^state[2][i]^state[3][i] s1 = state[0][i]^mul_by_02(state[1][i])^mul_by_03(state[2][i])^state[3][i] s2 = state[0][i]^state[1][i]^mul_by_02(state[2][i])^mul_by_03(state[3][i]) s3 = mul_by_03(state[0][i])^state[1][i]^state[2][i]^mul_by_02(state[3][i]) else: # decryption s0 = mul_by_0e(state[0][i])^mul_by_0b(state[1][i])^mul_by_0d(state[2][i])^mul_by_09(state[3][i]) s1 = mul_by_09(state[0][i])^mul_by_0e(state[1][i])^mul_by_0b(state[2][i])^mul_by_0d(state[3][i]) s2 = mul_by_0d(state[0][i])^mul_by_09(state[1][i])^mul_by_0e(state[2][i])^mul_by_0b(state[3][i]) s3 = mul_by_0b(state[0][i])^mul_by_0d(state[1][i])^mul_by_09(state[2][i])^mul_by_0e(state[3][i]) state[0][i] = s0 state[1][i] = s1 state[2][i] = s2 state[3][i] = s3 return state AddRoundKey ()
This transformation is inverse to itself due to the properties of the XOR operation:
(a XOR b) XOR b = a
Therefore, no changes need to be made. The set of round keys is formed in the same way as for encryption using the KeyExpansion () function, but round keys must be substituted in the reverse order.
Code
def add_round_key(state, key_schedule, round=0): for col in range(nk): # nb*round is a shift which indicates start of a part of the KeySchedule s0 = state[0][col]^key_schedule[0][nb*round + col] s1 = state[1][col]^key_schedule[1][nb*round + col] s2 = state[2][col]^key_schedule[2][nb*round + col] s3 = state[3][col]^key_schedule[3][nb*round + col] state[0][col] = s0 state[1][col] = s1 state[2][col] = s2 state[3][col] = s3 return state Now we have a comprehensive set of auxiliary transformation functions to write
Encryption function
def encrypt(input_bytes, key): # let's prepare our input data: State array and KeySchedule state = [[] for j in range(4)] for r in range(4): for c in range(nb): state[r].append(input_bytes[r + 4*c]) key_schedule = key_expansion(key) state = add_round_key(state, key_schedule) for rnd in range(1, nr): state = sub_bytes(state) state = shift_rows(state) state = mix_columns(state) state = add_round_key(state, key_schedule, rnd) state = sub_bytes(state) state = shift_rows(state) state = add_round_key(state, key_schedule, rnd + 1) output = [None for i in range(4*nb)] for r in range(4): for c in range(nb): output[r + 4*c] = state[r][c] return output Decryption function
def decrypt(cipher, key): # let's prepare our algorithm enter data: State array and KeySchedule state = [[] for i in range(nb)] for r in range(4): for c in range(nb): state[r].append(cipher[r + 4*c]) key_schedule = key_expansion(key) state = add_round_key(state, key_schedule, nr) rnd = nr - 1 while rnd >= 1: state = shift_rows(state, inv=True) state = sub_bytes(state, inv=True) state = add_round_key(state, key_schedule, rnd) state = mix_columns(state, inv=True) rnd -= 1 state = shift_rows(state, inv=True) state = sub_bytes(state, inv=True) state = add_round_key(state, key_schedule, rnd) output = [None for i in range(4*nb)] for r in range(4): for c in range(nb): output[r + 4*c] = state[r][c] return output These two functions take as input a list of bytes not encrypted or encrypted, and plaintext a string with a secret keyword.
Conclusion, interesting links
The article was quite long. I tried to dilute the text with pictures and, I hope, it was interesting for you and nobody got bored. The code presented in the article is not entirely exhaustive. I did not insert the global declaration of constant tables, small functions for MixColumns (), but explained only in words that they exist somewhere. Do not think that I am PR, but you can take the complete code glued together in the repository . There is also a modest CLI interface that allows you to simply specify the path to the file, enter the secret key and get the encrypted file in the same directory as the source (you can get the decrypted file in the same way). Encrypt for health!
And at the end it is necessary to say about one important nuance - padding or addition to the block. AES is a block encryption algorithm, the
encrypt()/decrypt() functions take exactly one block of input bytes as input (for our version with a 128-bit key, this is 16 bytes). At the end of the file can remain from 1 to 15 bytes, which do not form a solid block. They can simply, without encrypting, give to write to the final file, but in some cases, something important may be contained at the end of the file, and this option is not suitable. The second option was suggested to me by an article on Wikipedia about block ciphers.The simple addition of zero bits does not solve the problem, since the recipient cannot find the end of the payload. In addition, this option leads to the attacks of the Oracle additions. Therefore, in practice, a solution that is standardized as “Supplement Method 2” in ISO / IEC 9797-1 is applicable, adding a single bit to the end of the message and filling the remaining space with zeros. In this case, resistance to such attacks has been proven.
So I did (although the first option remained, just commented out. Suddenly, it will come in handy).
Selection of sources:
- Official documentation
- Very visual visual interpretation of the encryption part of the algorithm . Yes, the author does not sue me, made from there a couple of screenshots.
- Nowhere without Wikipedia
- Separate article about MixColumns () . It has tables with the results of multiplying the list of numbers 0 ... 255 by constants used in the cipher in the GF field (2 8 )
- Funny comic about the history of AES and the algorithm itself . It is a pity that I found it only when I already wrote the article.
Source: https://habr.com/ru/post/212235/
All Articles